【スマホで読む・わかりやすい】センター数学IA2017本試【解説・正解・問題】

第2問　解答・解説

ア 6　イ 2　ウ エ オ 2 6 4 または 6 2 4

カ キ ク ケ 2 3 2 3　コ サ 2 3

シ,ス,セ 1,4,6 (解答の順序は問わない)

ソ 4　タ 3　チ 2　ツ 0　テ 1

(1)

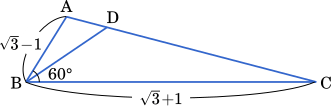
余弦定理より

$\text{AC}^2=(\sqrt{3}-1)^2+(\sqrt{3}+1)^2-2(\sqrt{3}-1)(\sqrt{3}+1)\cos60\degree$

$=3-2\sqrt{3}+1+3+2\sqrt{3}+1-2(3-1)\cdot\cfrac{1}{2}$

$=8-2=6$

AC＝$\sqrt{6}$

・・・ア

また，正弦定理より

$2R=\cfrac{\text{AC}}{\sin 60\degree}=\cfrac{\sqrt{6}}{\sin 60\degree}=\cfrac{\space\sqrt{6}\space}{\cfrac{\sqrt{3}}{2}}$

$=\cfrac{\space\sqrt{6}\times2\space}{\cfrac{\sqrt{3}}{2}\times2}=\cfrac{2\sqrt{6}}{\sqrt{3}}$

$=\cfrac{6\sqrt{2}}{3}=2\sqrt{2}$

$R=\sqrt{2}$

・・・イ

また，正弦定理より

$2\sqrt{2}=\cfrac{\text{BC}}{\sin\angle\text{BAC}}$

$\sin\angle\text{BAC}=\cfrac{\sqrt{3}+1}{2\sqrt{2}}$

$=\cfrac{(\sqrt{3}+1)\sqrt{2}}{4}=\cfrac{\sqrt{2}+\sqrt{6}}{4}$

・・・ウエオ

(2)

△ABD の面積は，公式 $S=\cfrac{1}{2}bc\sin A$ より

$\cfrac{1}{2}$ AB・AD・$\cfrac{\sqrt{2}+\sqrt{6}}{4}=\cfrac{\sqrt{2}}{6}$

AB・AD＝$\cfrac{\sqrt{2}}{6}\cdot\cfrac{8}{\sqrt{2}+\sqrt{6}}$

$=\cfrac{4\sqrt{2}(\sqrt{2}-\sqrt{6})}{3(\sqrt{2}+\sqrt{6})(\sqrt{2}-\sqrt{6})}$

$=\cfrac{8-8\sqrt{3}}{3(2-6)}$

$=\cfrac{8\sqrt{3}-8}{12}=\cfrac{2\sqrt{3}-2}{3}$

・・・カキクケ

よって

AD＝$\cfrac{2\sqrt{3}-2}{3}\cdot\cfrac{1}{\sqrt{3}-1}$

$=\cfrac{(2\sqrt{3}-2)(\sqrt{3}+1)}{3(\sqrt{3}-1)(\sqrt{3}+1)}$

$=\cfrac{6+2\sqrt{3}-2\sqrt{3}-2}{3(3-1)}$

$=\cfrac{4}{6}=\cfrac{2}{3}$

・・・コサ

〔2〕

⓪ $X$ と $V$ の間の相関は，$X$ と $Y$ の間の相関より弱い。よって，不適。

① 正しい。

② $X-V$ のグラフを見ると，$V$ が最大のデータは $X$ が 60 未満であり，不適。

③ $Y-V$ のグラフを見ると，$V$ が最大のデータは $Y$ が 50 以上 60 未満であり，不適。

④ 正しい。

⑤ $X-V$ のグラフを見ると，$X$ が 80 以上のデータで $V$ が 93 未満のものがある，よって，不適。

⑥ 正しい。

・・・シスセ

(2)

(i)

$X$ の分散を ${s_X}^2$，$D$ の分散を ${s_D}^2$，$X$ の平均を $\overline{X}$，$D$ の平均を $\overline{D}$ とすると

${s_X}^2=\cfrac{1}{n}\{(X_1-\overline{X})^2+\cdots+(X_n-\overline{X})^2\}$

${s_D}^2=\cfrac{1}{n}\{(D_1-\overline{D})^2+\cdots+(D_n-\overline{D})^2\}$

と表すことができる。$X$ の偏差を $D$ を用いて表すと

$X-\overline{X}=1.80(D-125.0)+60.0-\{1.80(\overline{D}-125.0)+60.0\}$

$=1.80(D-\overline{D})$

偏差の 2 乗を求めると

$(X-\overline{X})^2=3.24(D-\overline{D})^2$

よって，${s_X}^2$ は

${s_X}^2=3.24\cdot\cfrac{1}{n}\{(D-\overline{D})^2+\cdot+(D_n-\overline{D})^2\}$

${s_X}^2=3.24{s_D}^2$

と書き換えることができる。したがって，$X$ の分散は $D$ の分散の 3.24 倍。

・・・ソ

(ii)

$X$ と $Y$ の共分散を $s_{XY}$，$D$ と $Y$ の共分散を$s_{DY}$ とすると

$s_{XY}=\cfrac{1}{n}\{(X_1-\overline{X})(Y_1-\overline{Y})+\cdots+(X_n-\overline{X})(Y_n-\overline{Y})\}$

$s_{DY}=\cfrac{1}{n}\{(D_1-\overline{D})(Y_1-\overline{Y})+\cdots+(D_n-\overline{D})(Y_n-\overline{Y})\}$

(i)より，$X-\overline{X}=1.80(D-\overline{D})$ だから

$s_{XY}=1.80\cfrac{1}{n}\{(D_1-\overline{D})(Y_1-\overline{Y})+\cdots+(D_n-\overline{D})(Y_n-\overline{Y})\}$

よって，$s_{XY}=1.80s_{DY}$ となるので，$X$ と $Y$ の共分散は，$D$ と $Y$ の共分散の 1.80 倍。

・・・タ

(iii)

$X$ と $Y$ の相関係数を $r_1$，$D$ と $Y$ の相関係数を $r_2$，$X$ の標準偏差を $s_X$，$Y$ の標準偏差を $s_Y$，$D$ の標準偏差を $s_D$ とすると

$r_1=\cfrac{s_{XY}}{s_Xs_Y}$

$r_2=\cfrac{s_{DY}}{s_Ds_Y}$

(i)より

${s_X}^2=3.24{s_D}^2$

${s_X}=1.80{s_D}$

また，(ii)より $s_{XY}=1.80s_{DY}$ だから

$r1=\cfrac{1.80s_{DY}}{1.80s_Ds_y}=\cfrac{s_{DY}}{s_Ds_y}$

したがって，$r_1=r_2$ となるので，$X$ と $Y$ の相関係数は，$D$ と $Y$ の相関係数の 1 倍。

・・・チ

(3)

1 回目の $X+Y$ の最小値は 108.0 だから，グラフは A と a である。

また，図3から読み取れることとして正しいものは

⓪ 1 回目の $X+Y$ の四分位範囲は，2回目の $X+Y$ の四分位範囲よりわずかに小さい。したがって，不適。

① 正しい。

② 1 回目の $X+Y$ の最大値は，2 回目の $X+Y$ の最大値より大きい。したがって，不適。

③ 1 回目の $X+Y$ の最小値は，2 回目の $X+Y$ の最小値より大きい。したがって，不適。

・・・ツ

第2問　問題文

〔1〕△ABC において, AB = $\sqrt{3}-1$, BC = $\sqrt{3}+1$, ∠ABC = $60\degree$ とする。

(1) AC = $\sqrt{\boxed{\text{ア}}}$ であるから, △ABC の外接円の半径は $\sqrt{\boxed{\text{イ}}}$ であり

$\sin\angle\text{BAC}=\cfrac{\sqrt{\boxed{\text{ウ}}}+\sqrt{\boxed{\text{エ}}}}{\boxed{\text{オ}}}$

である。ただし, $\boxed{\text{ウ}}$, $\boxed{\text{エ}}$ の解答の順序は問わない。

(2) 辺 AC 上に点 D を, △ABD の面積が $\cfrac{\sqrt{2}}{6}$ になるようにとるとき

$\text{AB}\cdot\text{AD}=\cfrac{\boxed{\text{カ}}\sqrt{\boxed{\text{キ}}}-\boxed{\text{ク}}}{\boxed{\text{ケ}}}$

であるから, AD = $\cfrac{\boxed{\text{コ}}}{\boxed{\text{サ}}}$ である。

〔2〕スキージャンプは, 飛距離および空中姿勢の美しさを競う競技である。選手は斜面を滑り降り, 斜面の端から空中に飛び出す。飛距離 $D$(単位はm) から得点 $X$ が決まり, 空中姿勢から得点 $Y$ が決まる。ある大会における 58 回のジャンプについて考える。

(1) 得点 $X$, 得点 $Y$ および飛び出すときの速度 $V$(単位は km/h)について, 図1の 3 つの散布図を得た。

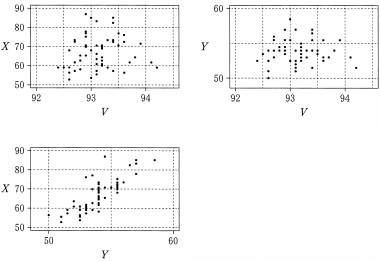
図 1

(出典:国際スキー連盟の Web ページにより作成)

次の $\boxed{\text{シ}}$, $\boxed{\text{ス}}$, $\boxed{\text{セ}}$ に当てはまるものを, 下の⓪~⑥のうちから一つずつ選べ。ただし, 解答の順序は問わない。

図1から読み取れることとして正しいものは, $\boxed{\text{シ}}$, $\boxed{\text{ス}}$, $\boxed{\text{セ}}$ である。

⓪ $X$ と $Y$ の間の相関は, $X$ と $Y$ の間の相関より強い。

① $X$ と $Y$ の間には正の相関がある。

② $V$ が最大のジャンプは, $X$ も最大である。

③ $V$ が最大のジャンプは, $Y$ も最大である。

④ $Y$ が最小のジャンプは, $X$ は最小ではない。

⑤ $X$ が 80 以上のジャンプは, すべて $V$ が 93 以上である。

⑥ $Y$ が 55 以上かつ $V$ が 94 以上のジャンプはない。
(2) 得点 $X$ は, 飛距離 $D$ から次の計算式によって算出される。

$X=1.80\times(D-125.0)+60.0$

次の $\boxed{\text{ツ}}$, $\boxed{\text{タ}}$, $\boxed{\text{チ}}$ にそれぞれ当てはまるものを, 下の⓪~⑥のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

・$X$ の分散は, $D$ の分散の $\boxed{\text{ソ}}$ 倍になる。

・$X$ と $Y$ の共分散は, $D$ と $Y$ の共分散の $\boxed{\text{タ}}$ 倍である。ただし, 共分散は, 2つの変量のそれぞれにおいて平均値からの偏差を求め, 偏差の積の平均値として定義される。

・$X$ と $Y$ の相関係数は, $D$ と $Y$ の相関係数の $\boxed{\text{チ}}$ 倍である。

⓪ $-125$　① $-1.80$　② $1$　③ $1.80$

④ $3.24$　⑤ $3.60$　⑥ $60.0$

(3) 58 回のジャンプは 29 名の選手が 2 回ずつ行ったものである。1 回目の $X+Y$(得点 $X$ と得点 $Y$ の和)の値に対するヒストグラムと 2 回目の $X+Y$ の値に対するヒストグラムは図2の A, B のうちのいずれかであ る。また, 1回目の $X+Y$ の値に対する箱ひげ図と2回目の $X+Y$ の値に対する箱ひげ図は図3の $a,b$ のうちのいずれかである。ただし, 1回目の $X+Y$ の最小値は 108.0 であった。

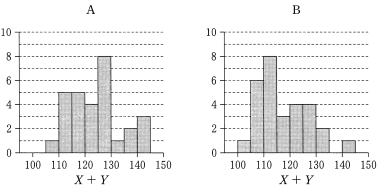
図2

(出典:国際スキー連盟の Web ページにより作成)

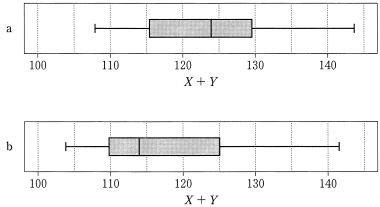
図3

(出典:国際スキー連盟の Web ページにより作成)

次の $\boxed{\text{ツ}}$ に当てはまるものを, 下の表の⓪~③のうちから一つ選べ。

1回目の $X+Y$ の値について, ヒストグラムおよび箱ひげ図の組合せとして正しいものは, $\boxed{\text{ツ}}$ である。

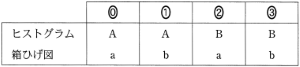
次の $\boxed{\text{テ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

図3から読み取れることとして正しいものは, $\boxed{\text{テ}}$ である。

⓪ 1回目の $X+Y$ の四分位範囲は, 2回目の $X+Y$ の四分位範囲より大きい。

① 1回目の $X+Y$ の中央値は, 2回目の $X+Y$ の中央値より大きい。

② 1回目の $X+Y$ の最大値は, 2回目の $X+Y$ の最大値より小さい。

③ 1回目の $X+Y$ の最小値は, 2回目の $X+Y$ の最小値より小さい。