【スマホで読む・わかりやすい】センター数学IA2016追試【解説・正解・問題】

解答・解説

ア イ 1 2　ウ エ 1 2　オ 1　カ キ 2 0

ク ケ 3 1　コ サ 1 0　シ 3　ス 0

セ 1

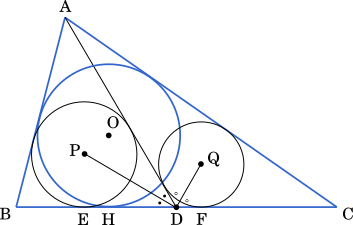
∠ADP = $\cfrac{1}{2}$ ∠ADB

∠ADQ = $\cfrac{1}{2}$ ∠ADC

・・・アイウエ

次に，PQ を直径とする円と点 D の関係について考えると

∠ADB $+$ ∠ADC = $180\degree$ より

$\cfrac{1}{2}$ ∠ADB $+$ $\cfrac{1}{2}$ ∠ADC = $90\degree$

∠ADP $+$ ∠ADQ = $90\degree$

したがって，点 D は PQ を直径とする円の円周上にある。

・・・オ

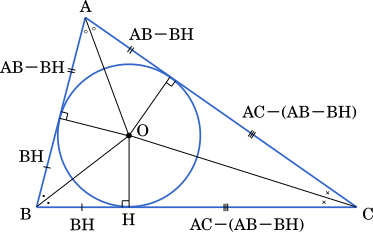
上の図より

BH + AC －( AB－BH ) = BC

2BH = AB + BC － AC

BH = $\cfrac{1}{2}$ ( AB + BC － AC ) $\cdots\cdots$①

・・・カキ

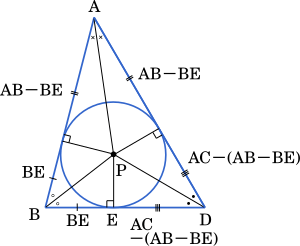
上の図より

BE + AD － ( AB － BE ) = BD

2BE = AB + BD － AD

BE = $\cfrac{1}{2}$ ( AB + BD － AD ) $\cdots\cdots$②

・・・クケ

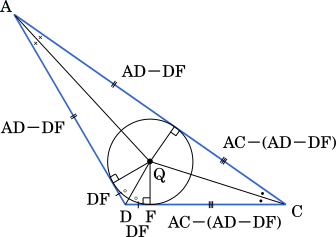
上の図より

DF + AC － ( AD － DF ) = DC

2DF = AD + DC － AC

DF = $\cfrac{1}{2}$ ( CD + AD － AC ) $\cdots\cdots$③

・・・コサ

次に，EH = BH － BE であり，①～③より

EH = $\cfrac{1}{2}$ ( AB + BC － AC － AB － BD + AD )

= $\cfrac{1}{2}$ ( BC － BD + AD － AC )

図より，BC － BD = CD だから

= $\cfrac{1}{2}$ ( CD + AD － AC)

= DF

したがって，EH = DF

・・・シ

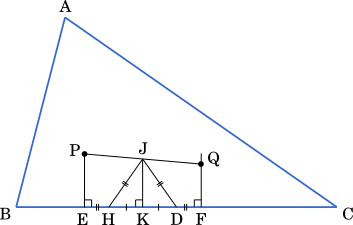
上の図より，PJ = QJ より EK = FK だから

EH = DF ならば，HK = DK が成り立つ。

・・・ス

これより，△JDH は二等辺三角形であり，JH = JD である。

さらに，上で求めたように，D は PQ を直径とする円の円周上にあるので，JD は円の半径である。したがって，JH も円の半径となるので，H は PQ を直径とする円の円周上にある。

・・・セ

[ad]

第5問　問題文

△ABC の内心を O, 内接円 O と辺 BC の接点を H とする。辺 BC 上に点 D をとる。ただし, D は B, C と異なる点とする。

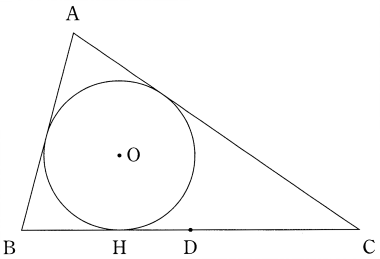
参考図

△ABD の内心を P とし, 内接円 P と辺 BD の接点を E とする。△ACD の内心を Q とし, 内接円 Q と辺 CD の接点を F とする。

PQ を直径とする円と 2 点 D, H の間の関係で △ABC がどのような形でも成り立つものを調べる。

次の $\boxed{\text{オ}}$ には下の⓪~③のうちから当てはまるものを一つ選べ。

∠ADP = $\cfrac{\boxed{\text{ア}}}{\boxed{\text{イ}}}$∠ADB, ∠ADQ = $\cfrac{\boxed{\text{ウ}}}{\boxed{\text{エ}}}$∠ADC であるから, PQ を直径とする円と点 D の関係について正しい選択肢は, $\boxed{\text{オ}}$ である。

⓪ D が辺 BC 上のどの位置にあっても, D はその円の内部にある。

① D が辺 BC 上のどの位置にあっても, D はその円周上にある。

② D が辺 BC 上のどの位置にあっても, D はその円の外部にある。

③ D が辺 BC 上のどの位置にあるかに応じて, D は, 円の内部, 円周上, 円の外部のどの場合もある。

次の $\boxed{\text{カ}}$~$\boxed{\text{サ}}$ に当てはまるものを, 下の⓪~③のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

BH = $\cfrac{1}{2}(\text{AB}+\boxed{\text{カ}}-\boxed{\text{キ}})\cdots\cdots$①

BE = $\cfrac{1}{2}(\text{AB}+\boxed{\text{ク}}-\boxed{\text{ケ}})\cdots\cdots$②

DF = $\cfrac{1}{2}(\text{CD}+\boxed{\text{コ}}-\boxed{\text{サ}})\cdots\cdots$③

である。

⓪ AC　① AD　② BC　③ BD

次の $\boxed{\text{シ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

①~③ から, EH = $\boxed{\text{シ}}$ であることがわかる。

⓪ FQ　① OP　② $\cfrac{1}{2}$EP　③ DF

次の $\boxed{\text{ス}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

PQ の中点を J とする。J を通り辺 BC に垂直な直線と BC の交点を K とすると, K は EF の中点であるから, HK = $\boxed{\text{ス}}$ である。

⓪ DK ① $\cfrac{1}{2}$JK　② EH　③ $\cfrac{1}{2}$FK

次の $\boxed{\text{セ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

HK = $\boxed{\text{ス}}$ に着目すると, PQ を直径とする円と点 H の関係について, 正しい選択肢は, $\boxed{\text{セ}}$ である。

⓪ D が辺 BC 上のどの位置にあっても, H はその円の内部にある。

① D が辺 BC 上のどの位置にあっても, H はその円周上にある。

② D が辺 BC 上のどの位置にあっても, H はその円の外部にある。

③ D が辺 BC 上のどの位置にあるかに応じて, H は, 円の内部, 円周上, 円の外部のどの場合もある。