【スマホで読む・わかりやすい】センター数学IA2016追試【解説・正解・問題】

第2問　解答・解説

ア 6　イ ウ 2 2　エ 3

オ カ キ 3 2 2　ク ケ 1 3

コサ 67

シ,ス 1,4 (解答の順序は問わない)

セ 2　ソ 3　タ 2

〔1〕

余弦定理より

$\text{BC}^2=1^2+(\sqrt{3})^2-2\cdot1\cdot\sqrt{3}\cos$∠BAC

$=1+3-2\sqrt{3}\Big(-\cfrac{\sqrt{3}}{3}\Big)$

$=4+2=6$

したがって，BC = $\sqrt{6}$

・・・ア

$\sin^2x+\cos^2x=1$ より

$\sin^2\angle\text{BAC}+\Big(-\cfrac{\sqrt{3}}{3}\Big)^2=1$

$\sin^2\angle\text{BAC}+\cfrac{1}{3}=1$

$\sin^2\angle\text{BAC}=\cfrac{2}{3}$

$\sin\angle\text{BAC}=\cfrac{\sqrt{6}}{3}$

△ACBの面積は $S=\cfrac{1}{2}bc\sin A$ を用いて

$S=\cfrac{1}{2}\cdot1\cdot\sqrt{3}\cdot\cfrac{\sqrt{6}}{3}$

$=\cfrac{\sqrt{2}}{2}$

・・・イウ

次に，BD は直径だから，正弦定理より

$2R=\cfrac{\text{BC}}{\sin\angle\text{BAC}}$

$=\cfrac{\space\sqrt{6}\space}{\cfrac{\sqrt{6}}{3}}=\cfrac{\space1\space}{\cfrac{1}{3}}=\cfrac{\space1\times3\space}{\cfrac{1}{3}\times3}=3$

したがって，BD = $3$

・・・エ

さらに，△BCD の面積を求めると，∠BCD = $90\degree$
だから，三平方の定理より

CD = $\sqrt{3^2-(\sqrt{6})^2}$

$=\sqrt{9-6}=\sqrt{3}$

したがって

$S=\cfrac{1}{2}\cdot\sqrt{6}\cdot\sqrt{3}=\cfrac{3\sqrt{2}}{2}$

・・・オカキ

また，AE と DE の比を求めると

円周角の定理より，△ABE ∽ △CDE，△ACE ∽ △DBE だから

AE : CE = 1: $\sqrt{3}$

CE : DE = $\sqrt{3}$ : 3

したがって，AE : DE = 1 : 3

$\cfrac{\text{AE}}{\text{DE}}=\cfrac{1}{3}$

・・・クケ

〔2〕

中央値は値の低いほうから 15, 16 番目のデータを足して 2 で割ったものである。ここでは表 2 を参考にして，15 ,16 番目のデータが 60 以上 70 未満の階級に含まれることを用いて，対象を絞るとよい。

表1 より，60 以上 70 未満のデータは

62 68 63 61 65 66

である。これを値の低い順に並べかえて

61 62 63 65 66 68

20 以上 60 未満のデータは $1+2+3+4=10$ 個だから，61 は 11 番目である。よって，15, 16 番目は 66, 68 である。

したがって，中央値は $\cfrac{66+68}{2}=67$

・・・コサ

〔3〕

(1)

① 四分位範囲が最も大きいのは C 組。

④ A 組を見ると，第1四分位数は 60, 第3四分位数は 80 だから，60 未満の人数と 80 以上の人数は同じである。

・・・シス

(2)

図1 より，C 組の第1四分位数は 60 以上 70 未満，第3四分位数は 80 以上 90 未満であることが分かる。

第1四分位数は 30 人を 15 人ずつに分け，15 人の中央の値だから，値の低いほうから 8 番目のデータである。同様に第3四分位数は，値の高いほうから 8 番目のデータである。

これをもとにして

⓪ 第3四分位数が 70 以上 80 未満に含まれるため，不適。

① 第1四分位数が 50 以上 60 未満に含まれるため，不適。

② 正しい。

③ 第3四分位数が 70 以上 80 未満に含まれるため，不適。

・・・セ

〔4〕

(1)

最大や最小を表すいくつかのデータをもとに考えるとよい。

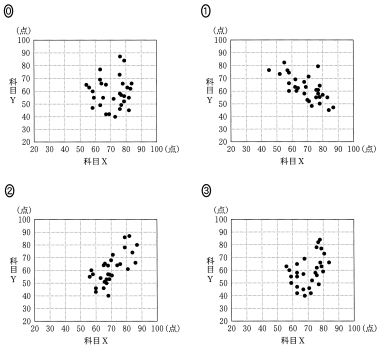
⓪ 科目 Y の点数が最も低い生徒は，科目 X が 68，科目 Y が 40 である。散布図では科目 Y の値が最も低い生徒は科目 X が 70 以上 80 未満に含まれるため，不適。

① 科目 X の最小値は 56 だから，不適。

② 科目 X の点数が最も低い生徒は，科目 X が 56，科目 Y が 63 である。散布図では科目 X の値が最も低い生徒は科目 Y が 50 以上 60 未満に含まれるため，不適。

③ 正しい。

・・・ソ

(2)

得点を $\cfrac{1}{2}$ にすると偏差が $\cfrac{1}{2}$ になるのは，得点と平均点がともに $\cfrac{1}{2}$ になるからである。分散を ${s_x}^2$，データを $x_1,x_2,\cdots,x_n$, 平均を $\overline{x}$ とすると

${s_x}^2=\cfrac{1}{n}\Big\{\Big(\cfrac{1}{2}x_1-\cfrac{1}{2}\overline{x}\Big)^2+\cdots+\Big(\cfrac{1}{2}x_n-\cfrac{1}{2}\overline{x}\Big)\Big\}$

$=\cfrac{1}{4}\cdot\cfrac{1}{n}\{(x_1-\overline{x})^2+\cdots+(x_n-\overline{x})\}$

よって，分散はもとの $\cfrac{1}{4}$ になる。

したがって，標準偏差はもとの値の $\sqrt{\cfrac{1}{4}}=\cfrac{1}{2}$

また，共分散 $s_{sy}$ を考えると

$s_{xy}=\cfrac{1}{n}\Big\{\Big(\cfrac{1}{2}x_1-\cfrac{1}{2}\overline{x}\Big)\Big(\cfrac{1}{2}y_1-\cfrac{1}{2}\overline{y}\Big)+\cdots+\Big(\cfrac{1}{2}x_n-\cfrac{1}{2}\overline{x}\Big)\Big(\cfrac{1}{2}y_n-\cfrac{1}{2}\overline{y}\Big)\Big\}$

$=\cfrac{1}{4}\cdot\cfrac{1}{n}\{(x_1-\overline{x})(y_1-\overline{y})+\cdots+(x_n-\overline{x})(y_n-\overline{y})\}$

よって，共分散の値はもとの値の $\cfrac{1}{4}$

したがって，②が正しい。

・・・タ

[ad]

第2問　問題文

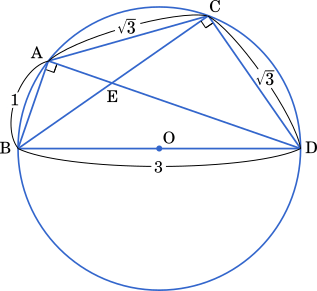
〔1〕△ABCにおいて, AB = $1$, CA = $\sqrt{3}$, $\cos$∠BAC = $-\cfrac{\sqrt{3}}{3}$ とすると, BC = $\sqrt{\boxed{\text{ア}}}$ であり, △ABC の面積は $\cfrac{\sqrt{\boxed{\text{イ}}}}{\boxed{\text{ウ}}}$ である。

△ABC の外接円の中心を O とし, 直線 OB と △ABC の外接円との交点で B と異なる点を D とすると, BD = $\boxed{\text{エ}}$ であり, △BCD の面積は $\cfrac{\boxed{\text{オ}}\sqrt{\boxed{\text{カ}}}}{\boxed{\text{キ}}}$ である。

直線 AD と直線 BC との交点を E とすると

$\cfrac{\text{AE}}{\text{DE}}=\cfrac{\boxed{\text{ク}}}{\boxed{\text{ケ}}}$

である。

〔2〕30 人の生徒に数学のテストを行った。次の表 1 は, その結果である。ただし, 表 1 の数値はすべて正確な値であるとして解答せよ。

表1 数学のテストの得点

次の表 2 は, 表 1 の 30 人のテストの得点を度数分布表にしたものである。

表2 30 人の生徒の得点の度数分布表

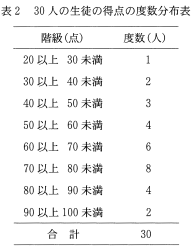
30 人の得点の中央値は $\boxed{\text{コサ}}$ である。

〔3〕 A 組から D 組の各組 30 人の生徒に対して理科のテストを行った。次の図 1 は, 各組ごとに理科のテストの得点を箱ひげ図にしたものである。

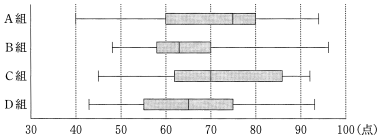
図1 A 組から D 組の理科のテストの箱ひげ図

(1) 次の $\boxed{\text{シ}}$, $\boxed{\text{ス}}$ に当てはまるものを, 下の⓪~⑤のうちから一つずつ選べ。ただし, 解答の順序は問わない。

図 1 の箱ひげ図について述べた文として誤っているものは $\boxed{\text{シ}}$ と $\boxed{\text{ス}}$ である。

⓪ A, B, C, D の 4 組全体の最高点の生徒がいるのは B 組である。

① A, B, C, D の 4 組で比べたとき, 四分位範囲が最も大きいのは A 組である。

② A, B, C, D の 4 組で比べたとき, 範囲が最も大きいのは A 組である。

③ A, B, C, D の 4 組で比べたとき, 第1四分位数と中央値の差が最も小さいのは B 組である。

④ A 組では, 60 点未満の人数は 80 点以上の人数よりも多い。

⑤ A 組と C 組で 70 点以下の人数を比べたとき, C 組の人数は A 組の人数以上である。

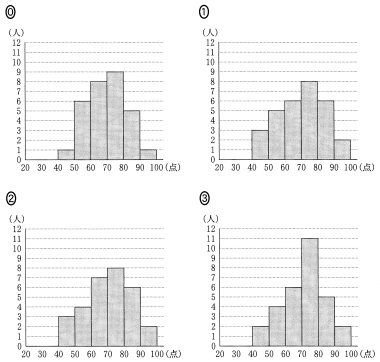
(2) 次の, $\boxed{\text{セ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

図 1 の C 組の箱ひげ図のもとになった得点をヒストグラムにしたとき, 対応するものは $\boxed{\text{セ}}$ である。ただし, ヒストグラムは〔2〕の表 2 の度数分布表と同じ階級を用いて作成した。

〔4〕次の表 3 は, あるクラスの生徒 30 人に行った科目 X と科目 Y のテストの得点であり, これらの平均値, 標準偏差, 共分散をまとめたものが下の表 4 である。

表3 科目 X と科目 Y の得点

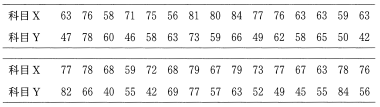
表4

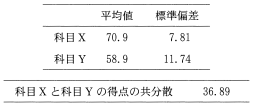
(共分散とは, 科目 X の得点の偏差と科目 Y の得点の偏差の積の平均値である)

(1) 次の $\boxed{\text{ソ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

科目 X と科目 Y の得点を散布図にしたものは $\boxed{\text{ソ}}$ である。

(2) 次の $\boxed{\text{タ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

表 3 の得点を $\cfrac{1}{2}$ にして 50 点満点の得点に換算した。例えば, 62 点であった場合は得点を 2 で割った値である 31 点とし, 63 点であった場合は 31.5 点とする。このとき,科目 X の得点の偏差と科目 Y の得点の偏差
は, 換算後, それぞれもとの得点の偏差の $\cfrac{1}{2}$ になる。したがって, 科目 X についてもとの標準偏差と換算後の標準偏差を比較し,さらにもとの共分散と換算後の共分散を比較すると, $\boxed{\text{タ}}$。

⓪ 換算後の標準偏差と共分散の値はともに, もとの値の $\cfrac{1}{2}$ になる

① 換算後の標準偏差と共分散の値はともに, もとの値の $\cfrac{1}{4}$ になる

② 換算後の標準偏差の値はもとの値の $\cfrac{1}{2}$ になり, 共分散の値はもとの値の $\cfrac{1}{4}$ になる

③ 換算後の標準偏差の値はもとの値の $\cfrac{1}{4}$ になり, 共分散の値はもとの 値の $\cfrac{1}{2}$ になる