【スマホで読む・わかりやすい】センター数学IA2016追試【解説・正解・問題】

第1問　解答・解説

ア イ 4 0　ウ エ 5 3　オ 1　カ 0

キ 4　ク 1　ケ 3　コ 2

サ シ ス 2 3 2

セソ 14　タ チ 1 3

〔1〕

(1)

命題 A の逆は

「$x$ ＞ 2」ならば「$x^2$ ＞ 2 または $x^3$ ＞ 0」

・・・アイ

また，命題 A の対偶を考える。

ド・モルガンの法則より $\overline{A\cup B}=\overline{A}\cap\overline{B}$ だから

「$x^2$ ＞ 2 または $x^3$ ＞ 0」の否定は「$x^2$ ≦ 2 かつ $x^3$ ＜ 0」となる。

$p\implies q$ の対偶は $\overline{q}\implies\overline{p}$ だから，命題 A の対偶は

「$x$ ≦ 2」 ならば「$x^2$ ≦ 2 かつ $x^3$ ≦ 0」

・・・ウエ

(2)

「$x^2$ ＞ 2 または $x^3$ ＞ 0」について考えると

$x^2$ ＞ 2

$x^2-2$ ＞ 0

$(x+\sqrt{2})(x-\sqrt{2})$ ＞ 0

$x$ ＜ $-\sqrt{2}$，$x$ ＞ $\sqrt{2}$

また

$x^3$ ＞ 0

$x$ ≠ 0 より

$x$ ＞ 0

よって，「$x^2$ ＞ 2 または $x^3$ ＞ 0」は「$x$ ＜ $-\sqrt{2}$ または $x$ ＞ 0」と書き換えることができる。したがって，命題 A は偽。

次に，命題 A の逆を考えると，「$x$ ＞ 2」ならば「$x$ ＜ $-\sqrt{2}$ または $x$ ＞ 0」となるので，命題 A の逆は真。

さらに，命題 A とその対偶の真偽は一致するので，命題 A の対偶は偽。したがって，当てはまる選択肢は①

・・・オ

(3)

(2)より，命題 A は偽であり，その逆は真だから，必要条件であるが，十分条件ではない。

・・・カ

〔2〕

$\sqrt{21}$ の整数部分を求めると

$\sqrt{16}\lt\sqrt{21}\lt\sqrt{25}$

$4\lt\sqrt{21}\lt5$

したがって，$\sqrt{21}$ の整数部分は 4

・・・キ

また，$\sqrt{31}$ の整数部分を求めると

$\sqrt{25}\lt\sqrt{31}\lt\sqrt{36}$

$5\lt\sqrt{31}\lt6$

したがって，$\sqrt{31}$ の整数部分は 5

このことから，$\sqrt{21},\sqrt{31}$ の小数部分は

$a=\sqrt{21}-4$

$c=\sqrt{31}-5$

となる。よって

$a-c=\sqrt{21}-4-\sqrt{31}+5=1+\sqrt{21}-\sqrt{31}$

・・・ク

$(1+\sqrt{21}-\sqrt{31})(1+\sqrt{21}+\sqrt{31})(9+2\sqrt{21})$

$=\{(1+\sqrt{21})-\sqrt{31}\}\{(1+\sqrt{21})+\sqrt{31}\}(9+2\sqrt{21})$

$=\{(1+\sqrt{21})^2-(\sqrt{31})^2\}(9+2\sqrt{21})$

$=(1+2\sqrt{21}+21-31)(9+2\sqrt{21})$

$=(2\sqrt{21}-9)(2\sqrt{21}+9)$

$=84-81=3$

・・・ケ

さらに，$a,b,c$ の大小を考える。

上の式に $a-c=1+\sqrt{21}-\sqrt{31}$ を当てはめると

$(a-c)(1+\sqrt{21}+\sqrt{31})(9+2\sqrt{21})=3$

したがって，$a-c$ は正の値をとるので，$c\lt a$

また，$\sqrt{23}$ の整数部分を求めると

$\sqrt{16}\lt\sqrt{23}\lt\sqrt{25}$

$4\lt\sqrt{23}\lt5$

よって，$\sqrt{23}$ の整数部分は 4

したがって，$b=\sqrt{23}-4$

また

$a-b=\sqrt{21}-4-\sqrt{23}+4=\sqrt{21}-\sqrt{23}$

$\sqrt{21}\lt\sqrt{23}$ だから，$a-b$ は負の値をとる。よって，$a\lt b$

したがって，$c\lt a\lt b$

・・・コ

〔3〕

①を平方完成すると

$y=a^2\Big(x^2-\cfrac{4}{a}x\Big)+b$

$=a^2\Big(x-\cfrac{2}{a}\Big)^2-4+b$

頂点の $x$ 座標が 1 以上 3 以下のとき

$1\leqq\cfrac{2}{a}\leqq3$

となる。

$1\leqq\cfrac{2}{a}$

$a\leqq2$

また

$\cfrac{2}{a}\leqq3$

$2\leqq 3a$

$a\geqq\cfrac{2}{3}$

となるので，$\cfrac{2}{3}\leqq a\leqq2$

・・・サシス

次に，②の解が存在する範囲を考えると，頂点が $x$ 軸より下にあればよいので

$-4+b\lt0$

$b\lt4$

・・・セソ

また，②の解が $1\lt x\lt 3$ になるとき，

$f(1)=0$, $f(3)=0$ である。

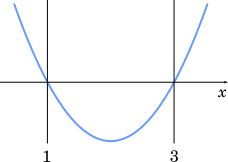
$f(1)=a^2-4a+b=0$

$f(3)=9a^2-12a+b=0$

式を連立すると

$8a^2-8a=0$

$a\not=0$ より

$a-1=0$

$a=1$

これを代入して

$1^2-4\cdot1+b=0$

$b=3$

したがって，$a=1$, $b=3$

・・・タチ

[ad]

第1問と第2問は必答。第3問から第5問はいずれか2問を選択し，解答する。

第1問　問題文

〔1〕実数 $x$ について

命題 A:「$x^2$ ＞ 2 または $x^3$ 0」ならば「$x$ ＞ 2」を考える。

(1) 次の$\boxed{\text{ア}}$~$\boxed{\text{エ}}$ に当てはまるものを, 下の⓪~⑤のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

命題 A の逆, 対偶を考えると次のようになる。

逆:「$\boxed{\text{ア}}$」ならば「$\boxed{\text{イ}}$」

対偶:「$\boxed{\text{ウ}}$」ならば「$\boxed{\text{エ}}$」

⓪ $x^2$ ＞ 2 または $x^2$ ＞ 0

① $x^2$ ＞ 2 かつ $x^3$ ＞ 0

② $x^2$ ≦ 2 または $x^3$ ≦ 0

③ $x^2$ ≦ 2 または $x^3$ ≦ 0

④ $x$ ＞ 0

⑤ $x$ ≦ 2

(2) 次の $\boxed{\text{オ}}$ に当てはまるものを, 下の⓪~⑥のうちから一つ選べ。

命題 A とその逆, 対偶のうち, $\boxed{\text{オ}}$が真である。

⓪ 命題 A のみ

① 命題 A の逆のみ

② 命題 A の対偶のみ

③ 命題 A とその対偶の二つのみ

④ 命題 A とその逆の二つのみ

⑤ 命題 A の逆と命題 A の対偶の二つのみ

⑥ 三つすべて

(3) 次の $\boxed{\text{カ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。

実数 $x$ についての条件「$x^2$ ＞ 2 または $x^3$ ＞ 0」は, 「$x$ ＞ 2」であるため の$\boxed{\text{カ}}$。

⓪ 必要条件であるが, 十分条件ではない

① 十分条件であるが, 必要条件ではない

② 必要十分条件である

③ 必要条件でも十分条件でもない

〔2〕$\sqrt{21}$ の整数部分は $\boxed{\text{キ}}$ である。

$\sqrt{21},\sqrt{23},\sqrt{31}$ の小数部分をそれぞれ $a,b,c$ とするとき

$a-c=\boxed{\text{ク}}+\sqrt{21}-\sqrt{31}$

であり

$(\boxed{\text{ク}}+\sqrt{21}-\sqrt{31})(\boxed{\text{ク}}+\sqrt{21}+\sqrt{31})(9+2\sqrt{27})=\boxed{\text{ケ}}$

となる。

次の $\boxed{\text{コ}}$ に当てはまるものを, 下の⓪~⑤のうちから一つ選べ。

$\boxed{\text{コ}}$ が成り立つ。

⓪ $a$ ＜ $b$ ＜ $c$　① $b$ ＜ $c$ ＜ $a$

② $c$ ＜ $a$ ＜ $b$　③ $a$ ＜ $c$ ＜ $b$

④ $c$ ＜ $b$ ＜ $a$　⑤ $b$ ＜ $a$ ＜ $c$

〔3〕$a,b$ は定数で, $a$ ≠ 0 とする。$x$ の2次関数

$y=a^2x^2-4ax+b\cdots\cdots$①

を考える。①のグラフの頂点の $x$ 座標が $1$ 以上 $3$ 以下になるような $a$ の値の範囲は $\cfrac{\boxed{\text{サ}}}{\boxed{\text{シ}}}$ ≦ $a$ ≦ $\boxed{\text{ス}}$ である。

下の $\boxed{\text{セ}}$ には, 次の⓪~④のうちから当てはまるものを一つ選べ。

⓪ ＞　① ＜　② ≧　③ ≦　④ ≠

$x$ の2次不等式

$a^2x^2-4ax+b\lt0\cdots\cdots$②

の解が存在するようなも $b$ 値の範囲は

$b\enspace\boxed{\text{セ}}\enspace\boxed{\text{ソ}}$

である。また②の解が 1 ＜ $x$ ＜ 3 になるような $a,b$ の値は

$a=\boxed{\text{タ}},\enspace b=\boxed{\text{チ}}$

である。