【スマホで読む・わかりやすい】センター数学IA2016本試【解説・正解・問題】

第2問　解答・解説

ア 7　イ ウエ 3 21　オ カ 7 3

キク 14　ケコ サ シ 49 3 2

ス,セ 0, 3 (解答の順序は問わない)

ソ 5

タ,チ 1,3 (解答の順序は問わない)

ツ 9　テ 8　ト 7

〔1〕

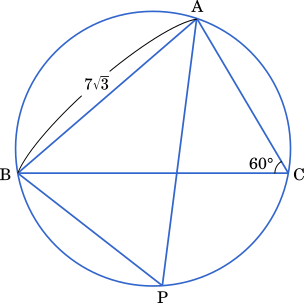
正弦定理より

$2R=\cfrac{7\sqrt{3}}{\sin60\degree}=\cfrac{7\sqrt{3}}{\cfrac{\sqrt{3}}{2}}=\cfrac{\enspace7\enspace}{\cfrac{1}{2}}$

$=14$

よって,$R=7$

・・・ア

(1)

2PA = 3PB より

$\cfrac{\text{PA}}{\text{PB}}=\cfrac{\space3\space}{2}$

よって，PA : PB = 3 : 2

また，円周角の定理より

∠ACB = ∠APB = $60\degree$

ここで，PA = $3x$, PB = $2x$ とおくと，余弦定理より

$(7\sqrt{3})^2=(3x)^2+(2x)^2-2\cdot3x\cdot2x\cos 60\degree$

$147=9x^2+4x^2-12x^2\cdot\cfrac{1}{2}$

$7x^2=147$

$x^2=21$

$x=\sqrt{21}$

したがって，PA = $3\sqrt{21}$

・・・イウエ

(2)

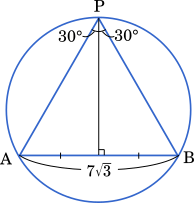
△PAB の面積が最大になるのは，P が AB の垂直二等分線上にあるときである。このとき，∠PAB = ∠PBA = $60\degree$ となり，△PAB は正三角形である。したがって，PA = $7\sqrt{3}$

・・・イウエ

(3)

$\sin$∠PBA が最大になるとき，$\sin$∠PBA = $1$ だから，∠PBA = $90\degree$ である。

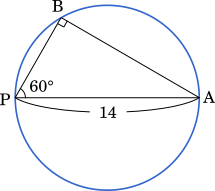
このとき，PA は直径だから，PA = $14$

・・・キク

△PAB は，辺の比が $1:2:\sqrt{3}$ の直角三角形だから

PB = $7$, AB = $7\sqrt{3}$

△PAB の面積を求めると

$S=\cfrac{1}{2}\cdot7\cdot7\sqrt{3}=\cfrac{49\sqrt{3}}{2}$

・・・ケコサシ

〔2〕

⓪ 正しい。

① 1日あたり平均降水量と購入額の間に相関関係は見られない。

② 平均湿度が高くなるほど購入額の散らばりは大きくなる傾向がある。

③ 正しい。

④ 平均最高気温と購入額，25℃以上の日数の割合と購入額の間にも正の相関が見られる。

・・・スセ

〔3〕

(1)

N市の最小値は $-10$ から $-5$ の間にあるので，N市は b である。また，M市の最大値は $40$ から $45$ の間にあるので，M市は a である。よって，⑤が正しい。

・・・ソ

(2)

東京とO市，東京とN市には正の相関が見られ，東京とM市には負の相関が見られる。したがって，①が正しい。

また，東京とO市の方が東京とN市よりも強い相関が見られる。したがって，③が正しい。

・・・タチ

(3)

N市(摂氏)のデータを $x_1,x_2,\cdots,x_n$，N市(華氏)のデータを $y_1,y_2,\cdots,y_n$ とし，N市(摂氏)の平均を $\overline{x}$，N市(華氏)の平均を $\overline{y}$ とすると

$X=\cfrac{1}{n}\{(x_1-\overline{x})^2+\cdots+(x_n-\overline{x})^2\}$

$Y=\cfrac{1}{n}\{(y_1-\overline{y})^2+\cdots+(y_n-\overline{y})^2\}$

となる。また

$y_n=\cfrac{9}{5}x_n+32$

$\overline{y}=\cfrac{9}{5}\overline{x}+32$

と表すことができる。よって

$y_n-\overline{y}=\cfrac{9}{5}x_n+32-\cfrac{9}{5}\overline{x}-32$

$=\cfrac{9}{5}(x_n-\overline{x})$

式を 2 乗して

$(y_n-\overline{y})^2=\cfrac{81}{25}(x_n-\overline{x})^2$

これを，$Y$ の式に代入すると

$Y=\cfrac{81}{25}\cdot\cfrac{1}{n}\{(x_1-\overline{x})^2+\cdots+(x_n-\overline{x})^2\}$

$=\cfrac{81}{25}X$

したがって

$\cfrac{Y}{X}=\cfrac{81}{25}$

・・・ツ

次に，東京(摂氏)のデータを $p_1,p_2,\cdots,p_n$ とすると

$Z=\cfrac{1}{n}\{(p_1-\overline{p})(x_1-\overline{x})+\cdots+(p_n-\overline{p})(x_n-\overline{x})\}$

$W=\cfrac{1}{n}\{(p_1-\overline{p})(y_1-\overline{y})+\cdots+(p_n-\overline{p})(y_n-\overline{y})\}$

となる。また，$y_n-\overline{y}=\cfrac{9}{5}(x_n-\overline{x})$ より

$W=\cfrac{9}{5}\cdot\cfrac{1}{n}\{(p_1-\overline{p})(x_1-\overline{x})+\cdots+(p_n-\overline{p})(x_n-\overline{x})\}$

$=\cfrac{9}{5}Z$

したがって

$\cfrac{W}{Z}=\cfrac{9}{5}$

・・・テ

相関係数の公式 $r=\cfrac{s_{xy}}{s_xs_y}$ ($s_{xy}$:
共分散，$s_x$:$x$の標準偏差，$s_y$:$y$の標準偏差)より

$U=\cfrac{Z}{s_p\sqrt{X}}$, $V=\cfrac{W}{s_p\sqrt{Y}}$

$\cfrac{V}{U}=\cfrac{\cfrac{W}{S_p\sqrt{Y}}}{\cfrac{Z}{S_p\sqrt{X}}}=\cfrac{\cfrac{W}{\sqrt{Y}}}{\cfrac{Z}{\sqrt{X}}}=\cfrac{W\sqrt{X}}{Z\sqrt{Y}}$

$=\cfrac{9}{5}\cdot\cfrac{5}{9}=1$

・・・ト

第2問　問題文

〔1〕 △ABC の辺の長さと角の大きさを測ったところ, AB = $7\sqrt{3}$ および ∠ACB = $60\degree$ であった。したがって, △ABC の外接円 O の半径は $\boxed{\text{ア}}$
である。

外接円 O の, 点 C を含む弧 AB 上で点 P を動かす。

(1) 2PA = 3PB となるのは PA = $\boxed{\text{イ}}\sqrt{\boxed{\text{ウエ}}}$ のときである。

(2) △PAB の面積が最大となるのは PA = $\boxed{\text{オ}}\sqrt{\boxed{\text{カ}}}$ のときである。

(3) $\sin$∠PBA の値が最大となるのは PA = $\boxed{\text{キク}}$ のときであり, このとき △PAB の面積は $\cfrac{\boxed{\text{ケコ}}\sqrt{\boxed{\text{サ}}}}{\boxed{\text{シ}}}$ である。

〔2〕次の 4 つの散布図は, 2003 年から 2012 年までの 120 か月の東京の月別データをまとめたものである。それぞれ, 1 日の最高気温の月平均(以下, 平均最高気温), 1 日あたり平均降水量, 平均湿度, 最高気温 25 °C 以上の日数の割合を横軸にとり, 各世帯の 1 日あたりアイスクリーム平均購入額 (以下, 購入額)を縦軸としてある。

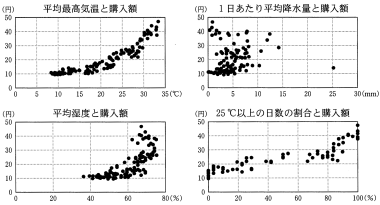
出典:総務省統計局(2013)『家計調査年報』,『過去の気象データ』(気象庁 Web ページ)などにより作成

次の $\boxed{\text{ス}}$, $\boxed{\text{セ}}$ に当てはまるものを, 下の⓪~④のうちから一つずつ選べ。ただし、解答の順序は問わない。

これらの散布図から読み取れることとして正しいものは, $\boxed{\text{ス}}$ と $\boxed{\text{セ}}$ である。

⓪ 平均最高気温が高くなるほど購入額は増加する傾向がある。

① 1 日あたり平均降水量が多くなるほど購入額は増加する傾向がある。

② 平均湿度が高くなるほど購入額の散らばりは小さくなる傾向がある。

③ 25°C 以上の日数の割合が 80% 未満の月は, 購入額が 30 円を超えていない。

④ この中で正の相関があるのは, 平均湿度と購入額の間のみである。

〔3〕世界 4 都市(東京, O市, N市, M市)の 2013 年の 365 日の各日の最高気温のデータについて考える。

(1) 次のヒストグラムは,東京, N市, M市のデータをまとめたもので, この3都市の箱ひげ図は下の a, b, c のいずれかである。

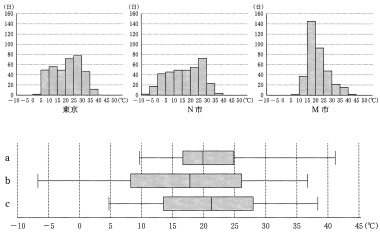
出典:『過去の気象データ』(気象庁 Web ページ)などにより作成

次の $\boxed{\text{ソ}}$ に当てはまるものを,下の⓪~⑤のうちから一つ選べ。

都市名と箱ひげ図の組合せとして正しいものは,　$\boxed{\text{ソ}}$ である。

⓪ 東京－a, N市－b, M市－c

① 東京－a, N市－c, M市－b

② 東京－b, N市－a, M市－c

③ 東京－b, N市－c, M市－a

④ 東京－c, N市－a, M市－b

⑤ 東京－c, N市－b, M市－a

(2) 次の 3 つの散布図は, 東京, O市, N市, M市の 2013 年の 365 日の各日の最高気温のデータをまとめたものである。それぞれ, O市, N市, M市の最高気温を縦軸にとり, 東京の最高気温を横軸にとってある。

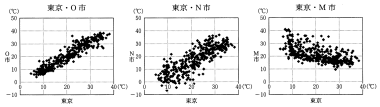
出典:『過去の気象データ』(気象庁 Web ページ)などにより作成

次の $\boxed{\text{タ}}$, $\boxed{\text{チ}}$ に当てはまるものを, 下の⓪~④のうちから一つずつ選べ。ただし, 解答の順序は問わない。

これらの散布図から読み取れることとして正しいものは, $\boxed{\text{タ}}$ と $\boxed{\text{チ}}$ である。

⓪ 東京とN市, 東京とM市の最高気温の間にはそれぞれ正の相関がある。

① 東京とN市の最高気温の間には正の相関, 東京とM市の最高気温の間には負の相関がある。

② 東京とN市の最高気温の間には負の相関, 東京とM市の最高気温の間には正の相関がある。

③ 東京とO市の最高気温の間の相関の方が, 東京とN市の最高気温の間の相関より強い。

④ 東京とO市の最高気温の間の相関の方が, 東京とN市の最高気温の間の相関より弱い。

(3)次の $\boxed{\text{ツ}},\boxed{\text{テ}},\boxed{\text{ト}}$ に当てはまるものを,下の⓪~⑨のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

N市では温度の単位として摂氏(°C)のほかに華氏(°F)も使われている。華氏(°F)での温度は, 摂氏(°C)での温度を $\cfrac{\space9\space}{5}$ 倍し, $32$ を加えると得られる。例えば,摂氏 10°Cは, $\cfrac{\space9\space}{5}$ し $32$ を加えることで華氏 50°F となる。

したがって, N市の最高気温について, 摂氏での分散を $X$, 華氏での分散を $Y$ とすると, $\cfrac{Y}{X}$ は $\boxed{\text{ツ}}$ になる。

東京(摂氏) と N市(摂氏) の共分散を $Z$, 東京(摂氏) と N市(華氏) の共分散を $W$ とすると, $\cfrac{W}{Z}$ は $\boxed{\text{テ}}$ になる(ただし, 共分散は 2 つの変量のそれぞれの偏差の積の平均値)。

東京(摂氏) と N市(摂氏)の相関係数を $U$, 東京(摂氏)と N市(華氏)の相関係数を $V$ とすると, $\cfrac{V}{U}$ は $\boxed{\text{ト}}$ になる。

⓪ $-\cfrac{81}{25}$　① $-\cfrac{9}{5}$　② $-1$　③ $-\cfrac{5}{9}$

④ $-\cfrac{25}{81}$　⑤ $\cfrac{25}{81}$　⑥ $\cfrac{5}{9}$　⑦ $1$

⑧ $\cfrac{9}{5}$　⑨ $\cfrac{81}{25}$