【スマホで読む・わかりやすい】センター数学IA2015追試【解説・正解・問題】
第1問 解答・解説
ア イ 5 4 ウ エ 3 4 オカ -3 キク -1
ケコ -1 サ 1 シス セソ -4 15
$G: y=-\cfrac{1}{4}x^2(x+a)^2+4(a+1)^2$
$=-\cfrac{1}{4}(x^2+2ax+a^2)+4a^2+8a+4$
$=-\cfrac{1}{4}(x^2+2ax+a^2-16a^2-32a-16)$
$=-\cfrac{1}{4}(x^2+2ax-15a^2-32a-16)$
$=-\cfrac{1}{4}\{x^2+2ax-(15a^2+32a+16)\}$
$=-\cfrac{1}{4}\{x^2+2ax-(3a+4)(5a+4)\}$
$=-\cfrac{1}{4}(x+5a+4)(x-3a-4)$
・・・アイウエ
(1)
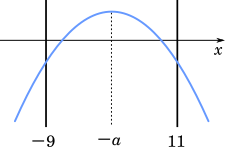
$f(x)=-\cfrac{1}{4}(x+5a+4)(x-3a-4)$ とおく。
問題に当てはまる条件を考えると
(i) グラフの軸が $-9$ と $11$ の間にある
(ii) 頂点が $x$ 軸より上にある
(iii) $x=9$ のとき,$y$ の値が負の数
(iv) $x=11$ のとき,$y$ の値が負の数
となる。
(i)
$-9\leqq -a \leqq 11$ だから
$-11\leqq a\leqq 9$
(ii)
$f(-a)=0$ のとき,グラフは $x$ 軸と 1 点で交わることになることに注意して
$f(-a)\gt0$
$-\cfrac{1}{4}(-a+5a+4)(-a-3a-4)\gt0$
$(4a+4)(-4a-4)\lt0$
$-16(a+1)(a+1)\lt0$
$(a+1)^2\gt0$
よって,$a\not =-1$
(iii)
$f(-9)\leqq0$
$-\cfrac{1}{4}(-9+5a+4)(-9-3a-4)\leqq0$
$(5a-5)(-3a-13)\geqq0$
$-5(a-1)(3a+13)\geqq0$
$(a-1)(3a+13)\leqq0$
$-\cfrac{13}{3}\leqq a\leqq 1$
(iv)
$f(11)\leqq0$
$-\cfrac{1}{4}(11+5a+4)(11-3a-4)\leqq0$
$(5a+15)(-3a+7)\geqq0$
$-5(a+3)(3a-7)\geqq0$
$(a+3)(3a-7)\leqq0$
$-3\leqq a\leqq\cfrac{7}{3}$
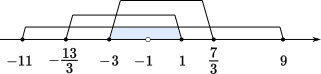
したがって
$-3\leqq a\lt1,\enspace-1\lt a\leqq 1$
・・・オカキクケコサ
(2)
$y$ 軸との交点を求める。$x=0$ を代入して
$y=-\cfrac{1}{4}a^2+4(a+1)^2$
$=-\cfrac{1}{4}a^2+4a^2+8a+4$
$=\cfrac{15}{4}a^2+8a+4$
平方完成すると
$=\cfrac{15}{4}\bigg(a^2+\cfrac{32}{15}a\bigg)+4$
$=\cfrac{15}{4}\bigg(a+\cfrac{16}{15}\bigg)^2-\cfrac{64}{15}+4$
$=\cfrac{15}{4}\bigg(a+\cfrac{16}{15}\bigg)^2-\cfrac{4}{15}$
したがって,$y$ の最小値は $\cfrac{-4}{15}$
・・・シスセソ
第1問~第3問は必答。第4問~第6問は2問を選択し,解答する。
第1問 問題文
$a$ を実数とする。2 次関数 $\displaystyle y=-\frac{1}{4}x^2$ のグラフを,$x$ 軸方向に $-a$,$y$ 軸方向に $4(a+1)^2$ だけ平行移動して得られるグラフを $G$ とする。$G$ の方程式は
$\displaystyle y=-\frac{1}{4}(x+\boxed{\text{ ア }}\space a+\boxed{\text{ イ }})(x-\boxed{\text{ ウ }}\space a-\boxed{\text{ エ }})$
と表せる。
(1) $G$ が $-9\leqq x\leqq 11$ の範囲で,$x$ 軸と相異なる 2 点で交わるような $a$ の値の範囲は
$\boxed{\text{ オカ }}\leqq a < \boxed{\text{ キク }}$,$\boxed{\text{ ケコ }} < a \leqq \boxed{\text{ サ }}$
である。
(2) $a$ が実数全体を動くとき,$G$ と $y$ 軸の交点の $y$ 座標の最小値は
$\displaystyle\frac{\boxed{\text{ シス }}}{\boxed{\text{ セソ }}}$
である。
SNSでシェア