【スマホで読む・わかりやすい】センター数学IA2015本試【解説・正解・問題】

第6問　解答・解説

アイ 10　ウ 5　エオ カ 10 3

キ ク 3 5　ケ コ 2 5

サ シ ス 5 5 4

方べきの定理を用いて

CE・CB = CA・CD

CE・CB = $5\cdot2=10$

・・・アイ

CB = $\sqrt{5}$ だから

CE・$\sqrt{5}=10$

CE = $\cfrac{10}{\sqrt{5}}=2\sqrt{5}$

よって

BE = $2\sqrt{5}-\sqrt{5}=\sqrt{5}$

・・・ウ

重心は 辺 AB を 2 : 1 に内分する点だから

AG = $\cfrac{2}{3}$ AB = $\cfrac{2}{3}\cdot5=\cfrac{10}{3}$

・・・エオカ

また，メネラウスの定理を用いて

$\cfrac{\text{EB}}{\text{BC}}\times\cfrac{\text{CA}}{\text{AD}}\times\cfrac{\text{DP}}{\text{PE}}=1$

$\cfrac{\sqrt{5}}{\sqrt{5}}\times\cfrac{5}{3}\times\cfrac{\text{DP}}{\text{PE}}=1$

$\cfrac{\text{DP}}{\text{PE}}=\cfrac{3}{5}\cdots\cdots$①

・・・キク

これにより，DP : PE = 3 : 5 であることが分かる。

次に ∠CAB = ∠CEDで，∠C が共通であることから，△ACB ∽ △ECD。対応する辺の比は等しいので

AC : EC = BA : DE

$5:2\sqrt{5}=5:\text{DE}$

$5\text{DE}=10\sqrt{5}$

DE = $2\sqrt{5}\cdots\cdots$②

・・・ケコ

①，②より

EP = $\cfrac{5}{8}\text{DE}$

$=\cfrac{5}{8}\cdot2\cdot\sqrt{5}=\cfrac{5\sqrt{5}}{4}$

・・・サシス

第6問　問題文

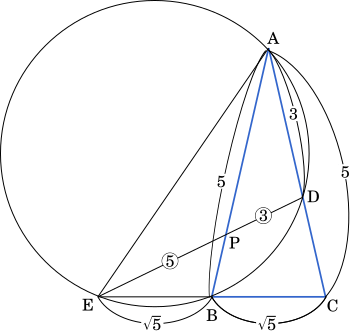
△ABC において，AB=AC=$5$，BC=$\sqrt{5}$ とする。辺 AC 上に点 D を AD=$3$ となるようにとり，辺 BC の B の側の延長と △ABD の外接円との交点で B と異なるものを E とする。

CE $\cdot$ CB=$\boxed{\text{ アイ }}$ であるから，BE=$\sqrt{\boxed{\text{ ウ }}}$ である。

△ACE の重心を G とすると，AG=$\displaystyle\frac{\boxed{\text{ エオ }}}{\boxed{\text{ カ }}}$ である。

AB と DE の交点を P とすると

$\displaystyle\frac{\text{DP}}{\text{EP}}=\frac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}\cdots$①

である。

△ABC と △EDC において，点 A，B，D，E は同一円周上にあるので ∠CAB=∠CED で，∠C は共通であるから

DE=$\displaystyle\boxed{\text{ ケ }}\sqrt{\boxed{\text{ コ }}}\cdots$②

である。

①，② から，EP=$\displaystyle\frac{\boxed{\text{ サ }}\sqrt{\boxed{\text{ シ }}}}{\boxed{\text{ ス }}}$ である。