【スマホで読む・わかりやすい】センター数学IA2015本試【解説・正解・問題】

第3問　解答・解説

ア 4

イ,ウ,エ,オ 0,2,3,5 (解答の順序は問わない)

カ,キ 0,2 (解答の順序は問わない)

ク 7

〔1〕

(1)

第3四分位数の含まれるデータは小さい方から 30, 31 番目のものだから，25m 以上 30m 未満。

・・・ア

(2)

第3四分位数は 25m 以上 30m 未満だから，⓪，②，③ が不適。また，第1四分位数の含まれるデータは小さい方から 10, 11 番目のものだから，15m 以上 20m 未満である。よって，②，③，⑤ が不適。したがって，⓪，②，③，⑤ が不適である。

・・・イウエオ

(3)

⓪ A－a

どの生徒の記録も下がっているなら，四分位数も下がるはずである。しかし，第1四分位数が増えているので，不適。

・・・カ

② C－c

上位 $\cfrac{1}{3}$ には第3四分位数と最大値が含まれるが，最大値が下がっているので，不適。

・・・キ

〔2〕

公式 $r=\cfrac{S_{xy}}{S_xS_y}$ を用いて相関係数を求めると

$r=\cfrac{54.30}{8.21\times6.98}=0.947\cdots=0.95$

・・・ク

第３問　問題文

〔1〕　ある高校 3 年生 1 クラスの生徒 40 人について，ハンドボール投げの飛距離のデータを取った。次の図 1 は，このクラスで最初に取ったデータのヒストグラムである。

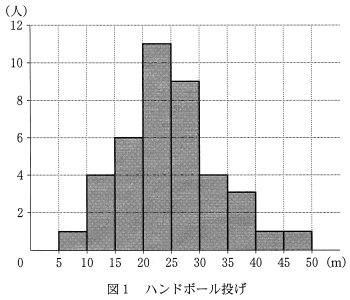
(1)　次の$\boxed{\text{ ア }}$ に当てはまるものを，下の⓪～⑧ のうちから一つ選べ。

この 40 人のデータの第 3 四分位数が含まれる階級は，$\boxed{\text{ ア }}$ である。

⓪ 5m 以上 10 m 未満　① 10 m 以上 15 m 未満

② 15 m 以上 20 m 未満　③ 20 m 以上 25 m 未満

④ 25 m 以上 30 m 未満　⑤ 30 m 以上 35 m 未満

⑥ 35 m 以上 40 m 未満　⑦ 40 m 以上 45 m 未満

⑧ 45 m 以上 50 m 未満

(2)　次の$\boxed{\text{ イ }}$～$\boxed{\text{ オ }}$ に当てはまるものを，下の⓪～⑤のうちから一つずつ選べ。ただし，$\boxed{\text{ イ }}$～$\boxed{\text{ オ }}$ の解答の順序は問わない。

このデータを箱ひげ図にまとめたとき，図 1 のヒストグラムと矛盾するものは，$\boxed{\text{ イ }}$，$\boxed{\text{ ウ }}$，$\boxed{\text{ エ }}$，$\boxed{\text{ オ }}$ である。

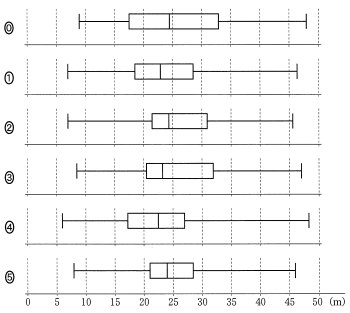
(3)　次の文章中の $\boxed{\text{ カ }}$，$\boxed{\text{ キ }}$ に入れるものとして最も適当なものを，下の⓪～③のうちから一つずつ選べ。ただし，$\boxed{\text{ カ }}$，$\boxed{\text{ キ }}$ の解答の順序は問わない。

後日，このクラスでハンドボール投げの記録を取り直した。次に示した A～D は，最初に取った記録から今回の記録への変化の分析結果を記述したものである。 a ～ d の各々が今回取り直したデータの箱ひげ図となる場合に，⓪～③の組み合せのうち分析結果と箱ひげ図が矛盾するものは，$\boxed{\text{ カ }}$，$\boxed{\text{ キ }}$ である。

⓪ A‐a　① B‐b

② C‐c　③ D‐d

A：どの生徒の記録も下がった。

B：どの生徒の記録も伸びた。

C：最初に取ったデータで上位 $\displaystyle\frac{1}{3}$ に入るすべての生徒の記録が伸びた。

D：最初に取ったデータで上位 $\displaystyle\frac{1}{3}$ に入るすべての生徒の記録は伸び，下位 $\displaystyle\frac{1}{3}$ に入るすべての生徒の記録は下がった。

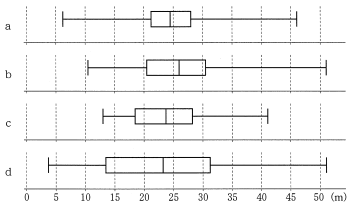
〔2〕　ある高校 2 年生 40 人のクラスで一人 2 回ずつハンドボール投げの飛距離のデータを取ることにした。次の図 2 は， 1 回目のデータを横軸に， 2 回目のデータを縦軸に取った散布図である。なお，一人の生徒が欠席したため，39 人のデータとなっている。

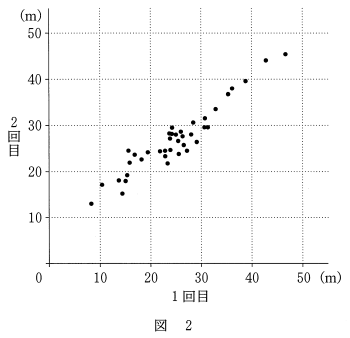
	平均値	中央値	分散	標準偏差
1回目のデータ	24.70	24.30	67.40	8.21
2回目のデータ	26.90	26.40	48.72	6.98

1 回目のデータと 2 回目のデータの共分散

54.30

(共分散とは 1 回目のデータの偏差と 2 回目のデータの偏差の積の平均である)

(1)　次の$\boxed{\text{ ク }}$ に当てはまるものを，下の⓪～⑨のうちから一つ選べ。

1 回目のデータと 2 回目のデータの相関係数に最も近い値は，$\boxed{\text{ ク }}$ である。

⓪ 0.67　① 0.71　② 0.75　③ 0.79　④ 0.83

⑤ 0.87　⑥ 0.91　⑦ 0.95　⑧ 0.99　⑨ 1.03