【スマホで読む・わかりやすい】センター数学IA2015本試【解説・正解・問題】

第3問　解答・解説

ア 1　イ 3　ウエ 29　オ 7　カ キ 3 2

ク ケ コサ 3 3 14　シ ス 7 2　セ 7

(1)

命題「($p_1$ かつ $p_2$) $\implies$ $(q_1$ かつ $q_2)$」の対偶は，ド・モルガンの法則を用いて

$\overline{p_1 \cap p_2}=\overline{p_1}\cup\overline{p_2}$

となることから

$(\overline{q_1}$ または $\overline{q_2})\implies(\overline{p_1}$ または $\overline{p_2})$ である。

・・・ア

(2)

30 以下の自然数において $(p_1$ かつ $p_2)$ は，ある素数に 2 加えたものも素数になる場合を考えるとよい。よって

$(p_1$ かつ $p_2)=\{3,5,11,17,29\}$

また，$(\overline{q_1}$ かつ $q_2)$ は順番を入れ替えて，$n+1$ が 6 の倍数だが 5 の倍数でないものを考えるとよい。これに当てはまるものは，$6,12,18,24$ である。求める集合はこれらから 1 除いたものであることに注意して

$(\overline{q_1}$ かつ $q_2)=\{5,11,17,23\}$

したがって，$3$ と $29$ は命題の反例となる。

・・・イウエ

〔2〕

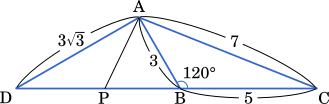
余弦定理を用いて

$\text{AC}^2=3^2+5^2-2\cdot3\cdot5\cos 120\degree$

$=9+25-30\bigg(-\cfrac{1}{2}\bigg)$

$=49$

$\text{AC}=7$

・・・オ

また

$\sin\angle\text{ABC}=\sin 120\degree=\cfrac{\sqrt{3}}{2}$

・・・カキ

正弦定理を用いて

$\cfrac{3}{\sin\angle{\text{BCA}}}=\cfrac{7}{\space\cfrac{\sqrt{3}}{2}\space}$

$\cfrac{3}{\sin\angle{\text{BCA}}}=\cfrac{14}{\sqrt{3}}$

$\sin\angle\text{BCA}=\cfrac{3\sqrt{3}}{14}$

・・・クケコサ

また，△APC の外接円の半径を $R$ とすると

$2R=\cfrac{7}{\sin\angle\text{APC}}$

$R=\cfrac{7}{2\sin\angle\text{APC}}$

よって，$\sin\angle\text{APC}$ が最大のとき，$R$ は最小となることが分かる。$\sin$ の最大値は $1$ だから

$R=\cfrac{7}{2\cdot1}=\cfrac{7}{2}$

・・・シス

また，$\sin\angle\text{APC}$ が最小のとき $R$ は最大となる。このとき，∠ADB の大きさを考えると，正弦定理より

$\cfrac{3}{\sin\angle\text{ADB}}=\cfrac{3\sqrt{3}}{\sin\angle\text{ABD}}$

$\cfrac{3}{\sin\angle\text{ADB}}=\cfrac{3\sqrt{3}}{\cfrac{\sqrt{3}}{2}}$

$\cfrac{3}{\sin\angle\text{ADB}}=6$

$\sin\angle\text{ADB}=\cfrac{1}{2}$

$\angle\text{ADB}=30\degree$

よって，$\angle\text{ADB}\lt\angle\text{ABD}$ となるので，$\sin$ の最小は点 P が点 D にあるときである。よって

$2R=\cfrac{7}{\space\cfrac{1}{2}\space}$

$R=7$

・・・セ

第２問　問題文

〔1〕　条件 $p_1$，$p_2$，$q_1$，$q_2$ の否定をそれぞれ $\overline{p_1}$，$\overline{p_2}$，$\overline{q_1}$，$\overline{q_2}$ と書く。

(1)　次の$\boxed{\text{ ア }}$ に当てはまるものを，下の⓪～③のうちから一つ選べ。

命題「($p_1$ かつ $p_2$)$\implies$($q_1$ かつ $q_2$)」の対偶は$\boxed{\text{ ア }}$である。

⓪　($\overline{p_1}$ または $\overline{p_2}$)$\implies$($\overline{q_1}$ または $\overline{q_2}$)

①　($\overline{q_1}$ または $\overline{q_2}$)$\implies$($\overline{p_1}$ または $\overline{p_2}$)

②　($\overline{q_1}$ かつ $p_2$)$\implies$($\overline{p_1}$ かつ $\overline{p_2}$)

③　($\overline{p_1}$ かつ $\overline{p_2}$)$\implies$($\overline{q_1}$ かつ $\overline{q_2}$)

(2)　自然数 $n$ に対する条件 $p_1$，$p_2$，$q_1$，$q_2$ を次のように定める。

$p_1:n$ は素数である

$p_2:n+2$ は素数である

$q_1:n+1$ は $5$ の倍数である

$q_2:n+1$ は $6$ の倍数である

$30$ 以下の自然数 $n$ のなかで$\boxed{\text{ イ }}$ と $\boxed{\text{ ウエ }}$ は
命題「($p_1$ かつ $p_2$)$\implies$($\overline{q_1}$ かつ $q_2$)」
の反例となる。

〔2〕　△ABC において，AB=$3$，BC=$5$，∠ABC=$120\degree$ とする。このとき，AC=$\boxed{\text{ オ }}$，$\sin$∠ABC=$\displaystyle\frac{\sqrt{\boxed{\text{ カ }}}}{\boxed{\text{ キ }}}$ であり，$\sin$∠BCA=$\displaystyle\frac{\boxed{\text{ ク }}\sqrt{\boxed{\text{ ケ }}}}{\boxed{\text{ コサ }}}$ である。

直線 BC 上に点 D を，AD=$3\sqrt{3}$ かつ ∠ADC が鋭角，となるようにとる。点 P を線分 BD 上の点とし，△APC の外接円の半径を $R$ とすると，$R$ のとり得る値の範囲は $\displaystyle\frac{\boxed{\text{ シ }}}{\boxed{\text{ ス }}} \leqq R \leqq \boxed{\text{ セ }}$ である。