【スマホで読む・わかりやすい】センター数学IA2015本試【解説・正解・問題】
第1問 解答・解説
ア,イ 1,3 ウ,エ 3,1 オ,カ 2,2
キク,ケ -1 2 コサ シ 13 4
①を平方完成すると
$y=-x^2+2x+2$
$y=-(x^2-2x)+2$
$=-(x-1)^2+1+2$
$-(x-1)^2+3$
頂点の座標は $(1,3)$
・・・アイ
①のグラフと $x$ 軸方向に $p$,$y$ 軸方向に $p$ だけ平行移動したものは
$f(x)=-(x-1-p)^2+3+q$
(1)
$2\leqq x\leqq 4$ において $f(2)$ で最大値をとるとき
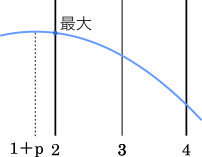
$1+p\leqq 2$
$p\leqq 1$
・・・ウエ
$f(2)$ で最小値をとるとき
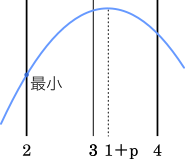
$1+p\geqq3$
$p\geqq2$
・・・オカ
(2)
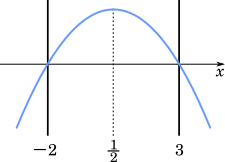
2 次不等式 $f(x)>0$ の解が $-2\lt x\lt 3$ になるとき,$f(x)$ は $x=-2,3$ で $x$ 軸と交わる。このとき,グラフの軸は $(-2+3)\div2=\cfrac{1}{2}$ となる。よって
$1+p=\cfrac{1}{2}$
$p=-\cfrac{1}{2}$
・・・クキケ
また,$f(-2)=0$ だから
$f(-2)=-(-2-1+\cfrac{1}{2})^2+3+q=0$
$-\cfrac{25}{4}+3+q=0$
$q=\cfrac{13}{4}$
・・・コサシ
第1問~第3問は必答。第4問~第6問はいずれか2問を選択し,解答。
第1問 問題文
2 次関数
$y=-x^2+2x+2\cdots$①
のグラフの頂点の座標は $(\boxed{\text{ ア }},\boxed{\text{ イ }})$ である。また
$y=f(x)\cdots$②
は $x$ の 2 次関数で,そのグラフは,①のグラフを $x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動したものであるとする。
(1) 下の $\boxed{\text{ ウ }}$,$\boxed{\text{ オ }}$ には,次の⓪~④のうちから当てはまるものを一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
⓪ $\gt$ ① $\lt$ ② $\geqq$ ③ $\leqq$ ④ $\not =$
$2\leqq x \leqq 4$ における $f(x)$ の最大値が $f(2)$ になるような $p$ の値の範囲は
$p\space\boxed{\text{ ウ }}\space\boxed{\text{ エ }}$
であり,最小値が $f(2)$ になるような $p$ の値の範囲は
$p\space\boxed{\text{ オ }}\space\boxed{\text{ カ }}$
である。
(2) 2 次不等式 $f(x) \gt 0$ の解が $-2 \lt x \lt 3$ になるのは
$\displaystyle p=\frac{\boxed{\text{ キク }}}{\boxed{\text{ ケ }}}$,$\displaystyle q=\frac{\boxed{\text{ コサ }}}{\boxed{\text{ シ }}}$
のときである。
SNSでシェア