【スマホで読む・わかりやすい】センター数学IA2014追試【解説・正解・問題】

第３問

△ABC を AB$=8$，BC$=12$，CA$=10$ を満たす三角形とする。辺 AB の中点を D，辺 BC の中点を E とする。このとき，$\sin$⁡∠DBE=$\cfrac{\boxed{\text{ ア }}\sqrt{\boxed{\text{ イ }}}}{\boxed{\text{ ウエ }}}$，△DBE の面積は $\cfrac{\boxed{\text{ オカ }}\sqrt{\boxed{\text{ キ }}}}{\boxed{\text{ ク }}}$ である。△DBE の内心を I とする。

(1)　内接円 I の半径は $\cfrac{\sqrt{\boxed{\text{ ケ }}}}{\boxed{\text{ コ }}}$ である。円 I と辺 BE の接点を L とすると，BL=$\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}$ であるので，BI$=\boxed{\text{ ス }}\sqrt{\boxed{\text{ セ }}}$ である。

三つの線分 AD ， CE ，DE すべてに接する円の中心を J とする。円 J と線分 CE との接点を X ， 線分 DE との接点を Y ， 線分 AD との接点を Z とする。

(2)　直線 BX ，BZ はともに点 B から円 J に引いた接線であるので， BX = BZ である。これより EX = $\cfrac{\boxed{\text{ ソ }}}{\boxed{\text{ タ }}}$ である。∠JBE=$\cfrac{\boxed{\text{ チ }}}{\boxed{\text{ ツ }}}$∠DBE，∠IBE=$\cfrac{\boxed{\text{ テ }}}{\boxed{\text{ ト }}}$∠DBE より BJ = $\boxed{\text{ ナ }}\sqrt{\boxed{\text{ ニ }}}$ である。

(3)　△DBE を含む平面と垂直で，直線 BJ を含む平面を考え，この平面内にある円で，線分 BJ を直径とするものを O とする。この円 O の円周上に点 K を， BJ と KI が直交するようにとると，KI=$\boxed{\text{ ヌ }}$ となるので，三角錐 KBDE の体積は $\boxed{\text{ ネ }}\sqrt{\boxed{\text{ ノ }}}$ となる。

[ad]

解答・解説

ア,イ,ウエ 5,7,16

オカ,キ,ク 15,7,4

ケ,コ 7,2　サ,シ 5,2

ス,セ 2,2　ソ,タ 3,2

チ,ツ 1,2　テ,ト 1,2

ナ,ニ 6,2　ヌ 4

ネ,ノ 5,7

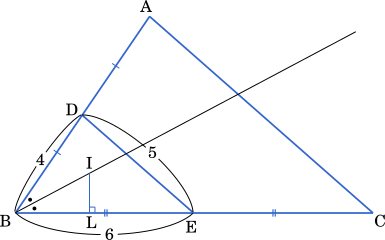
$\sin$ の値を直接求めることはできないので，いったん $\cos$ の値を求めた上で $\sin^2 x+\cos^2 x=1$ の公式を用いて $\sin$ の値を求めるとよい。

余弦定理より

$5^2=4^2+6^2-2\cdot4\cdot6\cos\angle\text{DBE}$

$25=16+36-48\cos\angle\text{DBE}$

$\cos\text{DBE}=\cfrac{27}{48}=\cfrac{9}{16}$

また $\sin^2 x+\cos^2 x=1$ より

$\sin^2\angle\text{DBE}+\bigg(\cfrac{9}{16}\bigg)^2=1$

$\sin^2\angle\text{DBE}=\cfrac{175}{256}$

$\sin\angle\text{DBE}=\cfrac{5\sqrt{7}}{16}$

△DBE の面積は

$S=\cfrac{1}{2}\cdot4\cdot6\cdot\sin\angle\text{DBE}$

$=12\cdot\cfrac{5\sqrt{7}}{16}$

$=\cfrac{15\sqrt{7}}{4}$

(1)

内接円の面積と半径の公式 $S=\cfrac{r}{2}(a+b+c)$ を用いて

$\cfrac{15\sqrt{7}}{4}=\cfrac{r}{2}(4+6+5)$

$\cfrac{15\sqrt{7}}{4}=\cfrac{15r}{2}$

$r=\cfrac{\sqrt{7}}{2}$

次に BL を求める。下の図のように合同な三角形を用いて BL を $x$ とおき、時計回りに辺の長さを順番においていくと、$x$ の値を求めることができる。

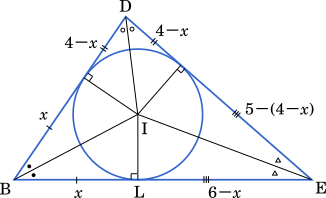
$5-(4-x)=6-x$

$1+x=6-x$

$2x=5$

$x=\cfrac{5}{2}$

したがって BL = $\cfrac{5}{2}$

次に三平方の定理を用いて BI を求めると

BI = $\sqrt{\bigg(\cfrac{5}{2}\bigg)^2+\bigg(\cfrac{\sqrt{7}}{2}\bigg)^2}$

$=\sqrt{\cfrac{25+7}{4}}$

$=\cfrac{\sqrt{32}}{2}$

$=2\sqrt{2}$

(2)

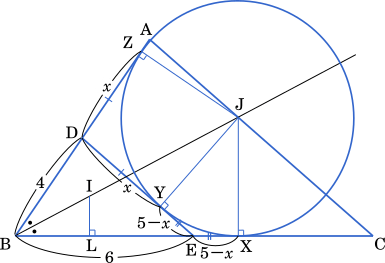
EX = EY，DY = DZ であることを利用するとよい。

DY = DZ = $x$ とおくと EY = $5-x$ となる。よって，EX = $5-x$ である。

BZ = BX より

$4+x=6+(5-x)$

$2x=7$

$x=\cfrac{7}{2}$

したがって

EX = $5-\cfrac{7}{2}=\cfrac{3}{2}$

また，直線 BJ は ∠ZBX の角二等分線だから

∠JBE = $\cfrac{1}{2}$ ∠DBE

∠IBE = $\cfrac{1}{2}$ ∠DBE

であり，これより △BLI ∽ △BXJ が成り立つ。これを用いて

BL : BX = BI : BJ

$\cfrac{5}{2}:6+\cfrac{3}{2}=2\sqrt{2}:$ BJ

$\cfrac{5}{2}:\cfrac{15}{2}=2\sqrt{2}:$ BJ

$\cfrac{15}{2}\cdot2\sqrt{2}=\cfrac{5}{2}$ BJ

$30\sqrt{2}=5$ BJ

BJ = $6\sqrt{2}$

(3)

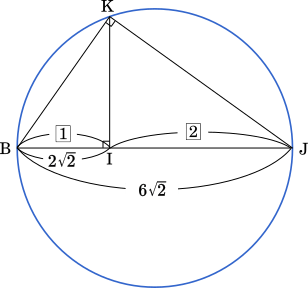
BI : IJ = 1 : 2 であり，また △BIK ∽ △BKJ であることを利用するとよい。よって

BI : BK = BK : BJ

$\text{BK}^2=2\sqrt{2}\cdot6\sqrt{2}$

$\text{BK}^2=24$

BK = $\sqrt{24}$

三平方の定理を用いて

KI = $\sqrt{(\sqrt{24})^2-(2\sqrt{2})^2}$

$=\sqrt{16}$

$=4$

また三角錐 KBDE の堆積は

$V=\cfrac{1}{3}\cdot\cfrac{15\sqrt{7}}{4}\cdot4$

$=5\sqrt{7}$