【スマホで読む・わかりやすい】センター数学IA2014追試【解説・正解・問題】

第２問

$a$，$b$，$c$ を定数とし，$a > 0$ とする。$x$ の 2 次関数

$y=ax^2+bx+c\cdots$①

は，$x=-1$ のとき $y=4$，$x=2$ のとき $y=7$ であるとする。
$b$，$c$ を $a$ で表すと

$b=\boxed{\text{ ア }}a+\boxed{\text{ イ }}$，$c=\boxed{\text{ ウエ }}a+\boxed{\text{ オ }}$

である。①のグラフの頂点の座標を $(p,q)$ とすると

$p=\cfrac{a-\boxed{\text{ カ }}}{\boxed{\text{ キ }} a}$，$q=\cfrac{\boxed{\text{ クケ }}a^2+\boxed{\text{ コサ }}a-\boxed{\text{ シ }}}{\boxed{\text{ ス }}a}$

である。

(1)　$a=2$ のとき，①のグラフを $x$ 軸方向に $\cfrac{\boxed{\text{ セソ }}}{\boxed{\text{ タ }}}$，$y$ 軸方向に $\cfrac{\boxed{\text{ チツ }}}{\boxed{\text{ テ }}}$ だけ平行移動すると， $y=2x^2$ のグラフに一致する。

(2)　①のグラフが $y$ 軸に関して対称になるとき，頂点の $y$ 座標は $\boxed{\text{ ト }}$ である。

(3)　関数①の最小値が $0$ であるとすると

$a=\cfrac{\boxed{\text{ ナニ }}\pm\boxed{\text{ ヌ }}\sqrt{\boxed{\text{ ネ }}}}{\boxed{\text{ ノ }}}$

である。

(4)　$1\leqq x\leqq 2$ における関数①の最小値が $0$ であるとすると

$a=\boxed{\text{ ハ }}$

である。

[ad]

解答・解説

ア,イ －,1　ウエ,オ －2,5

カ,キ 1,2

クケ,コサ,シ, －9,22,1

ス 4　セソ,タ －1,4

チツ,テ －7,8　ト 3

ナニ,ヌ,ネ,ノ 11,4,7,9

ハ 3

$y=ax^2+bx+c\cdots$①

$(x,y)=(-1,4)$ を代入して

$4=a-b+c$

$(x,y)=(2,7)$ を代入して

$7=4a+2b+c$

式を連立して

$3=3a+3b$

$a+b=1$

$b=-a+1$

これを代入して

$4=a+a-1+c$

$c=-2a+5$

次に頂点の座標を求める。①を平方完成して

$y=a\bigg(x^2+\cfrac{b}{a}x\bigg)+c$

$=a\bigg(x+\cfrac{b}{2a}\bigg)^2-a\bigg(\cfrac{b}{2a}\bigg)^2+c$

$=a\big(x+\cfrac{b}{2a}\bigg)^2-\cfrac{b^2}{4a}+c$

$p=-\cfrac{b}{2a}=\cfrac{a-1}{2a}$

$q=-\cfrac{b^2}{4a}+c$

$=-\cfrac{a^2-2a+1}{4a}+2a+5$

$=\cfrac{-9a^2+22a-1}{4a}$

(1)

$a=2$ のとき

$p=\cfrac{2-1}{2\cdot2}=\cfrac{1}{4}$

$q=\cfrac{-9\cdot2^2+22\cdot2-1}{4\cdot2}$

$=\cfrac{7}{8}$

$y=2x^2$ は頂点が原点となるので，①のグラフを $x$ 軸方向に $-\cfrac{1}{4}$，$y$ 軸方向に $-\cfrac{7}{8}$ だけ平行移動すればよい。

(2)

グラフが $y$ 軸に関して対称になるとき，軸は $0$ である。よって，$p=0$ となる。

$\cfrac{a-1}{2a}=0$

$a=1$

これを $q$ に代入して

$q=\cfrac{-9+22-1}{4}=3$

(3)

①は頂点で最小値をとるので

$q=\cfrac{-9a^2+22a-1}{4a}=0$

$9a^2-22a+1=0$

$a=\cfrac{11\pm\sqrt{121-9}}{9}$

$=\cfrac{11\pm4\sqrt{7}}{9}$

(4)

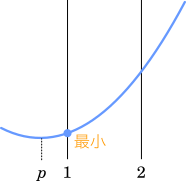
(i) $p\lt1$ のとき，$x=1$ で最小値 $0$ をとる。

このとき

$p\lt1$

$\cfrac{a-1}{2a}\lt1$

$a-1\lt2a$

$a\gt-1$

となり，条件 $a\gt0$ に合う。よって①に $x=1$ を代入して

$a+b+c=0$

$a-a+1-2a+5=0$

$a=3$

(ii) $1\leqq p\lt2$ のとき $x=p$ で最小値 $0$ をとる。

このとき

$1\leqq p$

$1\leqq\cfrac{a-1}{2a}$

$2a\leqq a-1$

$a\leqq -1$

これは $a\gt0$ に合わない。よって，(i) とあわせて考えると $p\lt1$ のときのみ $1\leqq x\leqq 2$ で最小値が $0$ になる。よって，$p\geqq2$ の場合については考えなくてもよい。

したがって $a=3$