【スマホで読む・わかりやすい】センター数学IA2014本試【解説・正解・問題】

第４問

下の図は，ある町の街路図の一部である。

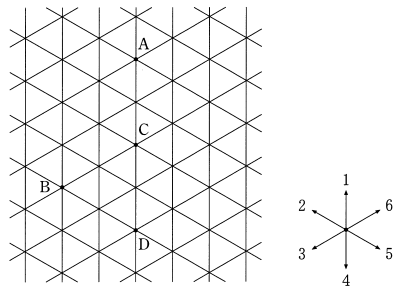
ある人が，交差点 A から出発し，次の規則に従って，交差点から隣の交差点への移動を繰り返す。

①　街路上のみを移動する。

②　出発前にサイコロを投げ，出た目に応じて右図の 1 〜 6 の矢印の方向の隣の交差点に移動する。

③　交差点に達したら，再びサイコロを投げ，出た目に応じて図の 1 〜 6 の矢印の方向の隣の交差点に移動する。（一度通った道を引き返すこともできる。）

④　交差点に達するたびに， ③ と同じことを繰り返す。

(1)　交差点 A を出発し， 4 回移動して交差点 B にいる移動の仕方について考える。この場合，3 の矢印の方向の移動と 4 の矢印の方向の移動をそれぞれ 2 回ずつ行うので，このような移動の仕方は$\boxed{\text{ ア }}$ 通りである。

(2)　交差点 A を出発し，3 回移動して交差点 C にいる移動の仕方は $\boxed{\text{ イ }}$ 通りある。

(3)　交差点 A を出発し，6 回移動することを考える。このとき，交差点 A を出発し，3 回の移動が終わった時点で交差点 C にいて，次に 3 回移動して交差点 D にいる移動の仕方は $\boxed{\text{ ウエ }}$ 通りあり，その確率は $\cfrac{\boxed{\text{ オ }}}{\boxed{\text{ カキクケ }}}$ である。

(4)　交差点 A を出発し，6 回移動して交差点 D にいる移動の仕方について考える。

・1 の矢印の向きの移動を含むものは $\boxed{\text{ コ }}$ 通りある。

・2 の矢印の向きの移動を含むものは $\boxed{\text{ サシ }}$ 通りある。

・6 の矢印の向きの移動を含むものも $\boxed{\text{ サシ }}$ 通りある。

・上記 3 つ以外の場合，4 の矢印の向きの移動は $\boxed{\text{ ス }}$ 回だけに決まるので，移動の仕方は $\boxed{\text{ セソ }}$ 通りある。

よって，交差点 A を出発し，6 回移動して交差点 D にいる移動の仕方は $\boxed{\text{ タチツ }}$ 通りある。

解答・解説

ア $6$

イ $6$

ウエ $36$

オ,カキクケ $1,1296$

コ $6$

サシ $30$

ス $2$

セソ $90$

タチツ $156$

(1)

4 つの矢印の並べ方は $4!$ 通りあるが，同じ矢印がそれぞれ 2 つずつあるので，$2!$ で割るとよい。

$\cfrac{4!}{2!\cdot2!}=\cfrac{1\cdot2\cdot3\cdot4}{2\cdot2}=6$ 通り

(2)

3，4，5 の矢印を 1 回ずつ使うので

$3!=6$ 通り

(3)

(2)より C までの移動の仕方は $6$ 通り

C から D までの移動の仕方も(2)と同様だから $6$ 通り

したがって，$6\times6=36$ 通り

またその確率を求めると，サイコロを 6 回投げるときの全事象は $6^6$ であることに注意して

$\cfrac{36}{6^6}=\cfrac{1}{6^4}=\cfrac{1}{1296}$

(4)

(i) 1 の矢印を含む場合

1 の矢印を 1 回，4 の矢印を 5 回使うので

$\cfrac{6!}{1!\cdot5!}=6$ 通り

(ii) 2 の矢印を含む場合

2 の矢印を 1 回，4 の矢印を 4 回，5 の矢印を 1 回使うので

$\cfrac{6!}{1!\cdot4!\cdot1!}=30$ 通り

(iii) 6 の矢印を含む場合

$30$ 通り

(iv) 上記 3 つ以外の場合，3 の矢印を 2 回，4 の矢印を 2 回，5 の矢印を 2 回使うので，4 の矢印の向きの移動は 2 回だけに決まる。よって

$\cfrac{6!}{2!\cdot2!\cdot2!}=90$ 通り

したがって，6 回移動して交差点 D にいる移動の仕方は

$6+30+30+90=156$ 通り