【スマホで読む・わかりやすい】センター数学IA2014本試【解説・正解・問題】

第３問

△ABC は，AB$=4$，BC$=2$，$\cos$∠ABC$=\cfrac{1}{4}$ を満たすとする。このとき

CA$=\boxed{\text{ ア }}$，$\cos⁡$∠BAC$=\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}$，$\sin$∠BAC$=\cfrac{\sqrt{\boxed{\text{ エオ }}}}{\boxed{\text{ カ }}}$

であり，△ABC の外接円 O の半径は $\cfrac{\boxed{\text{ キ }}\sqrt{\boxed{\text{ クケ }}}}{\boxed{\text{ コサ }}}$ である。 ∠ABC の二等分線と ∠BAC の二等分線の交点を D，直線 BD と辺 AC の交点を E，直線 BD と円 O との交点で B と異なる交点を F とする。

(1)　このとき

AE=$\cfrac{\boxed{\text{ シ }}}{\boxed{\text{ ス }}}$，BE$=\cfrac{\boxed{\text{ セ }}\sqrt{\boxed{\text{ ソタ }}}}{\boxed{\text{ チ }}}$，BD$=\cfrac{\boxed{\text{ ツ }}\sqrt{\boxed{\text{ テト }}}}{\boxed{\text{ ナ }}}$

となる。

(2)　△EBC の面積は △EAF の面積の $\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$ 倍である。

(3)　角度に注目すると，線分 FA，FC，FD の関係で正しいものは $\boxed{\text{ ネ }}$ であることが分かる。

$\boxed{\text{ ネ }}$ に当てはまるものを，次の⓪～⑤のうちから一つ選べ。

⓪ FA < FC = FD　① FA=FC < FD

② FC < FA = FD　③ FD < FC < FA

④ FA = FC = FD　⑤ FD < FC = FA

解答・解説

ア $4$

イ,ウ $7,8$

エオ,カ $15,8$

キ,クケ,コサ $8,15,15$

シ,ス $8,3$

セ,ソタ,チ $2,10,3$

ツ,テト,ナ $2,10,5$

ニ,ヌ $5,8$

ネ $4$

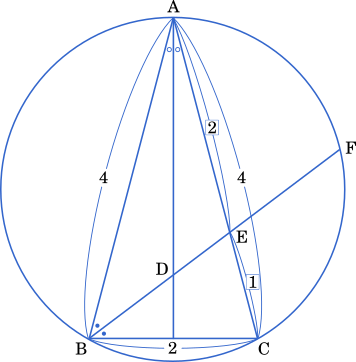
余弦定理を用いて

$\text{CA}^2=4^2+2^2-2\cdot4\cdot2\cos\angle\text{ABC}$

$=16+4-16\cdot\cfrac{1}{4}$

$=16$

CA $=4$

また

$2^2=4^2+4^2-2\cdot4\cdot4\cos\angle{\text{BAC}}$

$4=16+16-32\cos\angle\text{BAC}$

$32\cos\angle\text{BAC}=28$

$\cos\angle{\text{BAC}}=\cfrac{7}{8}$

さらに $\sin^2 x+\cos^2 x=1$ を用いて

$\sin^2\angle\text{BAC}+\bigg(\cfrac{7}{8}\bigg)^2=1$

$\sin^2\angle\text{BAC}+\cfrac{49}{64}=1$

$\sin^2\angle\text{BAC}=\cfrac{15}{64}$

$\sin\angle\text{BAC}=\cfrac{\sqrt{15}}{8}$

次に，正弦定理より

$2R=\cfrac{2}{\enspace\cfrac{\sqrt{15}}{8}\enspace}$

$=\cfrac{2\times8}{\enspace\cfrac{\sqrt{15}}{8}\times8\enspace}$

$=\cfrac{16}{\sqrt{15}}=\cfrac{16\sqrt{15}}{15}$

$R=\cfrac{8\sqrt{15}}{15}$

(1)

BE は $\angle{\text{ABC}}$ の二等分線だから

AE : EC = $4:2=2:1$

が成り立つ。よって

AE = $4\times\cfrac{2}{3}=\cfrac{8}{3}$

また，余弦定理を用いて

$\text{BE}^2=4^2+\bigg(\cfrac{8}{3}\bigg)^2-2\cdot4\cdot\cfrac{8}{3}\cos\angle\text{BAE}$

$=16+\cfrac{64}{9}-\cfrac{64}{3}\cdot\cfrac{7}{8}$

$=\cfrac{40}{9}$

BE $=\cfrac{\sqrt{40}}{3}=\cfrac{2\sqrt{10}}{3}$

次に，AD は $\angle\text{BAC}$ の二等分線だから

BD:DE = $4:\cfrac{8}{3}=3:2$

が成り立つ。よって

BD $=\cfrac{2\sqrt{10}}{3}\times\cfrac{3}{5}=\cfrac{2\sqrt{10}}{5}$

(2)

円周角の定理より，∠CBF = ∠CAF，∠ACB = ∠AFB だから，△EBC ∽ △EAF が成り立つ。辺の比を求めると

BE : AE $=\cfrac{2\sqrt{10}}{3}:\cfrac{8}{3}$

$=\sqrt{10}:4$

ここで，(辺の比)$^2$=(面積の比) を利用して

△EBC : △EAF $=(\sqrt{10})^2:4^2=10:16=5:8$

したがって，△EBC の面積は △EAF の面積の $\cfrac{5}{8}$ 倍である。

(3)

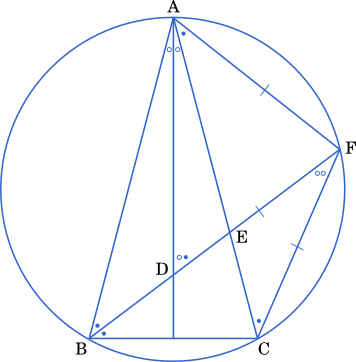
三角形の外角の性質より ∠ABD + ∠BAD = ∠ADF だから，△ADF は ∠FAD = ∠DAF の二等辺三角形である。よって，FA = FD が成り立つ。

また，円周角の定理より ∠CBF = ∠CAF，∠ABF = ∠ACF だから，△ACF は ∠CAF = ∠ACF の二等辺三角形である。よって，FA = FC が成り立つ。

したがって，FA=FC=FD である。