【スマホで読む・わかりやすい】センター数学IA2014本試【解説・正解・問題】

第２問

$a$ を定数とし，$x$ の 2 次関数

$y=x^2+2ax+3a^2-6a-36\cdots$①

のグラフを $G$ とする。$G$ の頂点の座標は

$(\boxed{\text{ ア }}a,\boxed{\text{ イ }}a^2-\boxed{\text{ ウ }}a-\boxed{\text{ エオ }})$

である。$G$ と $y$ 軸との交点の $y$ 座標を $p$ とする。

(1)　$p=-27$ のとき，$a$ の値は $a=\boxed{\text{ カ }}$，$\boxed{\text{ キク }}$ である。$a=\boxed{\text{ カ }}$ のときの①のグラフを $x$ 軸方向に$\boxed{\text{ ケ }}$，$y$ 軸方向に$\boxed{\text{ コ }}$ だけ平行移動すると，$a=\boxed{\text{ キク }}$ のときの①のグラフに一致する。

(2)　下の$\boxed{\text{ ス }}$，$\boxed{\text{ セ }}$，$\boxed{\text{ ノ }}$，$\boxed{\text{ ハ }}$ には，次の⓪～③のうちから当てはまるものを一つずつ選べ。ただし，同じものを繰り返し選んでもよい。

⓪ $ > $　① $ < $　② $\geqq$　③ $\leqq$

$G$ が $x$ 軸と共有点を持つような $a$ の値の範囲を表す不等式は

$\boxed{\text{ サシ }}\space\boxed{\text{ ス }}\space a \boxed{\text{ セ }}\space\boxed{\text{ ソ }}\cdots$②

である。$a$ が②の範囲にあるとき，$p$ は，$a=\boxed{\text{ タ }}$ で最小値 $\boxed{\text{ チツテ }}$ をとり，$a=\boxed{\text{ ト }}$ で最大値 $\boxed{\text{ ナニ }}$ をとる。

$G$ が $x$ 軸と共有点を持ち，さらにそのすべての共有点の $x$ 座標が $-1$ より大きくなるような $a$ の値の範囲を表す不等式は

$\boxed{\text{ ヌネ }}\space\boxed{\text{ ノ }}\space a \boxed{\text{ ハ }}\cfrac{\boxed{\text{ ヒフ }}}{\boxed{\text{ ヘ }}}$

である。

解答・解説

ア,イ,ウ,エオ $-,2,6,36$

カ,キク $3,-1$

ケ $4$

コ $8$

サシ $-3$

ス,セ $3,3$

ソ $6$

タ $1$

チツテ $-39$

ト $6$

ナニ $36$

ヌネ $-3$

ノ,ハ $3,1$

ヒフ,ヘ $-7,3$

$f(x)=x^2+2ax+3a^2-6a-36$ として平方完成すると

$f(x)=(x+a)^2-a^2+3a^2-6a-36$

$=(x+a)^2+2a^2-6a-36$

したがって，頂点の座標は

$(-a,2a^2-6a-36)$

(1)

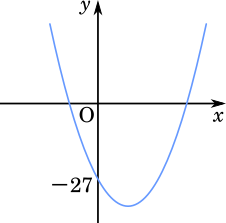
$p=-27$ のとき，$G$ は $(0,-27)$ を通過するので，$f(x)$ に代入して

$-27=a^2+2a^2-6a-36$

$3a^2-6a-9=0$

$a^2-2a-3=0$

$(a-3)(a+1)=0$

$a=3,-1$

次に，$a=3$ のときの頂点の座標は

$(-3,2\cdot3^2-6\cdot3-36)$

$=(-3,-36)$

また $a=1$ のときの頂点の座標は

$(1,2(-1)^2-6(-1)-36)$

$=(1,-28)$

したがって，$x$ 軸方向に $-3$ から $1$ へ $4$，$y$ 軸方向に $-36$ から $-28$ へ $8$ だけ平行移動すると一致する。

(2)

$G$ が $x$ 軸と共有点を持つとき，判別式 $D\geqq0$ が成り立つので

$\cfrac{D}{4}=a^2-3a^2+6a+36\geqq0$

$-2a^2+6a+36\geqq0$

$a^2-3a-18\leqq0$

$(a+3)(a-6)\leqq0$

$-3\leqq a \leqq 6$

次に，$f(0)=p$ だから

$f(0)=3a^2-6a-36=p$

平方完成すると

$p=3(a^2-2a)-36$

$=3(a-1)^2-3-36$

$=3(a-1)^2-39$

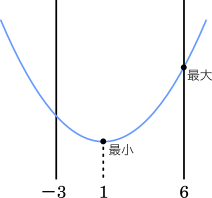
$a=1$ で最小値 $-39$

また最大値を求めると $a=6$ を代入して

$p=3(6-1)^2-39$

$=75-39=36$

したがって $a=6$ で最大値 $36$ をとる。

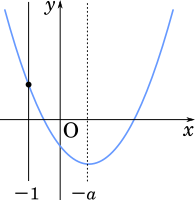
さらに，$G$ が $x$ 軸と共有点を持ち，さらにそのすべての共有点の $x$ 座標が $-1$ より大きくなるような $a$ の値の範囲の条件は

・軸が$-1$ より大きい。

・$f(-1) > 0$

である。

$f(-1) > 0$

頂点の座標より，軸は $-a$ となるので

$-a > -1$

$a < 1$ また $f(-1)=1-2a+3a^2-6a-36 > 0$

$3a^2-8a-35 > 0$

$(3a+7)(a-5) > 0$

$a < -\cfrac{7}{3},\space a > 5$

これと $-3\leqq a \leqq 6$ に注意して

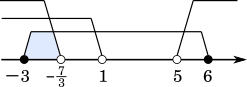
したがって

$-3\leqq a < -\cfrac{7}{3}$