【スマホで読む・わかりやすい】センター数学IA2013追試【解説・正解・問題】

第３問

△ABC において，AB=$2\sqrt{3}$，BC=$\sqrt{6}$，CA=$3$ とする。このとき

$\cos⁡$∠ACB=$\cfrac{\sqrt{\boxed{\text{ ア }}}}{\boxed{\text{ イウ }}}$，$\sin$⁡∠ABC=$\cfrac{\sqrt{\boxed{\text{ エオカ }}}}{\boxed{\text{ キク }}}$

であり，△ABC の外接円 O の半径は $\cfrac{\boxed{\text{ ケ }}\sqrt{\boxed{\text{ コサ }}}}{\boxed{\text{ シス }}}$ である。

円 O の点 B における接線と点 C における接線の交点を P とし，線分 AP と辺 BC の交点を D とする。また，点 A を通り辺 BC と平行な直線と，直線 PB，PC との交点をそれぞれ X，Y とする。

(1)　下の $\boxed{\text{ セ }}$ ～ $\boxed{\text{ タ }}$ には，次の ⓪～⑥ のうちから当てはまるものを一つずつ選べ。ただし，同じものを繰り返し選んでもよい。

⓪ ∠BAC　① ∠ABC　② ∠ACB　③ $90\degree$

④ ∠BPC　⑤ ∠BAD　⑥ ∠CAD

XY と BC は平行であるから，∠XAB=$\boxed{\text{ セ }}$ である。また，XP が円 O に接するので，∠XBA=$\boxed{\text{ ソ }}$ である。したがって，∠AXB=$\boxed{\text{ タ }}$ であり，AX=$\boxed{\text{ チ }}\sqrt{\boxed{\text{ ツ }}}$ となる。

(2)　(1)と同様に，AY=$\cfrac{\boxed{\text{ テ }}\sqrt{\boxed{\text{ ト }}}}{\boxed{\text{ ナ }}}$ となる。XY と BC は平行であるから，$\cfrac{\text{DC}}{\text{BD}}=\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$ である。よって，DC=$\cfrac{\boxed{\text{ ネ }}\sqrt{\boxed{\text{ ノ }}}}{\boxed{\text{ ハ }}}$ となる。
これより，AD=$\cfrac{\boxed{\text{ ヒフ }}}{\boxed{\text{ ヘ }}}{\boxed{\text{ ホ }}}$ となる。

解答・解説

ア $6$　イウ $12$　エオカ $138$　キク $12$

ケ $6$　コサ $46$　シス $23$

セ $1$　ソ $2$　タ $0$　チ $2$　ツ $6$

テ $3$　ト $6$　ナ $2$

ニ $3$　ヌ $4$　ネ $3$　ノ $6$　ハ $7$

ヒフ $12$　ヘ $3$　ホ $7$

余弦定理を用いて

$(2\sqrt{3})^2=3^2+(\sqrt{6})^2-2\cdot3\cdot6\cos\angle\text{ACB}$

$12=9+6-6\sqrt{6}\cos\angle\text{ACB}$

$6\sqrt{6}\cos\angle\text{ACB}=3$

$\cos\angle\text{ACB}=\cfrac{1}{2\sqrt{6}}=\cfrac{\sqrt{6}}{12}$

また $\sin^2 x+\cos^2 x=1$ より

$\sin^2\angle\text{ACB}+\bigg(\cfrac{\sqrt{6}}{12}\bigg)^2=1$

$\sin^2\angle\text{ACB}=1-\cfrac{6}{144}=\cfrac{138}{144}$

$\sin\angle\text{ACB}=\cfrac{\sqrt{138}}{12}$

さらに正弦定理を用いて

$2R=\cfrac{2\sqrt{3}}{\cfrac{\sqrt{138}}{12}}=\cfrac{24\sqrt{3}}{\sqrt{138}}=\cfrac{24}{\sqrt{46}}$

$=\cfrac{12\sqrt{46}}{23}$

$R=\cfrac{6\sqrt{46}}{23}$

(1)

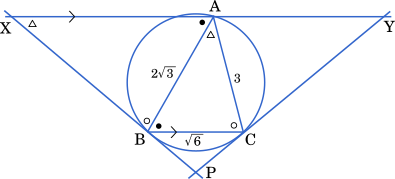
錯角が等しいので $\angle\text{XAB}=\angle\text{ABC}$

また接弦定理より $\angle\text{XBA}=\angle\text{ACB}$

これより△XAB と △ABC において，2 組の角がそれぞれ等しいので

△XAB ∽ △ABC

が成り立つ。したがって，$\angle\text{AXB}=\angle\text{BAC}$

辺の比を求めると

AB : BC = $2\sqrt{3}:\sqrt{6}=2:\sqrt{2}$

よって

AX : AB = $2:\sqrt{2}$

AX : $2\sqrt{3}$ = $2:\sqrt{2}$

$\sqrt{2}\text{XA}=4\sqrt{3}$

AX = $\cfrac{4\sqrt{3}}{\sqrt{2}}=2\sqrt{6}$

(2)

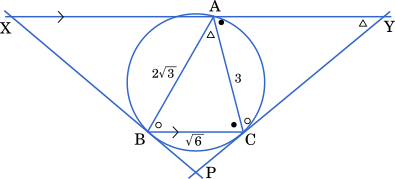
(1)と同様にして △XAC ∽ △ABC となる。辺の比を求めると

AC : CB = AY : CA = $3:\sqrt{6}$

AY : $3=3\sqrt{6}$

$\sqrt{6}\text{AY}=9$

AY = $\cfrac{9\sqrt{6}}{6}=\cfrac{3\sqrt{6}}{2}$

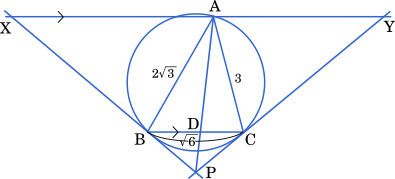
$\cfrac{\text{DC}}{\text{BD}}=\cfrac{\text{AY}}{\text{XA}}=\cfrac{\cfrac{3\sqrt{6}}{2}}{\enspace2\sqrt{6}\enspace}=\cfrac{\cfrac{3}{2}}{\enspace2\enspace}=\cfrac{3}{4}$

よって BD : DC = $4:3$ だから

DC = $\sqrt{6}\times\cfrac{3}{7}=\cfrac{3\sqrt{6}}{7}$

これより，余弦定理を用いて AD を求めると

$\text{AD}^2=3^2+\bigg(\cfrac{3\sqrt{6}}{7}\bigg)^2-2\cdot3\cdot\cfrac{3\sqrt{6}}{7}\cdot\cfrac{\sqrt{6}}{12}$

$=9+\cfrac{54}{49}-\cfrac{9}{7}$

$=\cfrac{441+54-63}{49}$

$=\cfrac{432}{49}$

$\text{AD}=\cfrac{\sqrt{432}}{7}=\cfrac{12\sqrt{3}}{7}$