【スマホで読む・わかりやすい】センター数学IA2013追試【解説・正解・問題】

第２問

$b$ を定数とするとき，$x$ の2次関数

$y=x^2-2bx-\cfrac{4}{3}b+\cfrac{5}{9}\cdots$①

のグラフの頂点の座標は

$\bigg(b,\boxed{\text{ ア }}b^2-\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}b+\cfrac{\boxed{\text{ エ }}}{\boxed{\text{ オ }}}\bigg)$

である。

(1)　$a,c$ を定数とする。 ①のグラフが，関数 $y=ax^2-2x+c$ のグラフと原点に関して対称となるのは，$a=\boxed{\text{ カキ }}$，$b=\boxed{\text{ ク }}$，$c=\cfrac{\boxed{\text{ ケ }}}{\boxed{\text{ コ }}}$ のときである。また $b= \boxed{\text{ ク }}$ のとき，①のグラフと，関数 $y=x( x+4)$ のグラフを $x$ 軸方向に $s$ ，$y$ 軸方向に $t$ だけ平行移動したグラフとが一致するのは

$s=\boxed{\text{ サ }}, t=\cfrac{\boxed{\text{ シス }}}{\boxed{\text{ セ }}}$

のときである。

(2)　下の $\boxed{\text{ ナ }}$，$\boxed{\text{ ハ }}$，$\boxed{\text{ ヒ }}$ には，次の ⓪～④ のうちから当てはまるものを一つずつ選べ。ただし，同じものを繰り返し選んでもよい。

⓪ $ > $　① $ < $　② $\geqq$　③ $\leqq$　④ $=$

$0\leqq x \leqq 1$ の範囲における関数①の値の最小値を $m$ とする。

$b < 0$ のとき $m=-\cfrac{4}{3}b+\cfrac{5}{9}$ $0 \leqq b \leqq 1$ のとき $m= \boxed{\text{ ア }}b^2-\cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}b+\cfrac{\boxed{\text{ エ }}}{\boxed{\text{ オ }}}$ $b > 1$ のとき $m=-\cfrac{\boxed{\text{ ソタ }}}{\boxed{\text{ チ }}} b+\cfrac{\boxed{\text{ ツテ }}}{\boxed{\text{ ト }}}$

である。したがって $m < 0$ となる $b$ の値の範囲は

$b\space\boxed{\text{ ナ }}\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$

である。

また，$0\leqq x \leqq 1$ の範囲で①のグラフと $x$ 軸が異なる2点で交わる $b$ の値の範囲は

$\cfrac{\boxed{\text{ ネ }}}{\boxed{\text{ ノ }}}\boxed{\text{ ハ }}\space b\space \boxed{\text{ ヒ }}\cfrac{\boxed{\text{ フ }}}{\boxed{\text{ ヘホ }}}$

である。

解答・解説

ア $-$　イ $4$　ウ $3$　エ $5$　オ $9$

カキ $-1$　ク $1$　ケ $7$　コ $9$

サ $3$　シス $20$　セ $9$

ソタ $10$　チ $3$　ツテ $14$　ト $9$

ナ $0$　ニ $1$　ヌ $3$

ネ $1$　ノ $3$　ハ $1$　ヒ $3$　フ $5$　ヘホ $12$

$f(x)=x^2-2bx-\cfrac{4}{3}b+\cfrac{5}{9}$ とおいて平方完成すると

$f(x)=(x-b)^2-b^2-\cfrac{4}{3}b+\cfrac{5}{9}$

したがって頂点の座標は

$\bigg(b,\space-b^2-\cfrac{4}{3}b+\cfrac{5}{9}\bigg)$

(1)

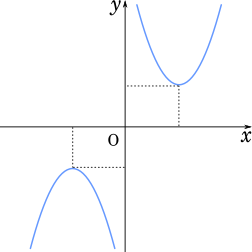
$f(x)$ と原点対称の式は

$y=-(x+b)^2+b^2+\cfrac{4}{3}b-\cfrac{5}{9}$

$=-x^2-2bx-b^2+b^2+\cfrac{4}{3}b-\cfrac{5}{9}$

$=-x^2-2bx+\cfrac{4}{3}b-\cfrac{5}{9}$

これと，$y=ax^2-2x+c$ を比べると

$a=-1$

$-2=-2b$ より $b=1$

$c=\cfrac{4}{3}b-\cfrac{5}{9}$ より

$c=\cfrac{4}{3}-\cfrac{5}{9}=\cfrac{7}{9}$

次に $y=x(x+4)$ を平方完成すると

$y=x^2+4x$

$=(x+2)^2-4$

頂点は $(-2,\space-4)$ である。

また $b=1$ のとき，$f(x)$ の頂点は

$\bigg(1,\space-1^2-\cfrac{4}{3}\cdot1+\cfrac{5}{9}\bigg)$

=$\bigg(1,-\space\cfrac{16}{9}\bigg)$

$(-2,\space-4)$ を $x$ 軸方向に $s$，$y$ 軸方向に $t$ だけ平行移動したものが $\bigg(1,-\space\cfrac{16}{9}\bigg)$ と一致するので

$-2+s=1$ より $s=3$

$-4+t=-\cfrac{16}{9}$ より $t=\cfrac{20}{9}$

(2)

(i) $b < 0$ のとき

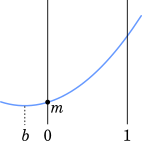
$x=0$ で最小となるので

$m < 0$ となる範囲を求めると

$-\cfrac{4}{3}b+\cfrac{5}{9} < 0$

$-12b+5 < 0$ $12b > 5$

$b > \cfrac{5}{12}$

これは $b < 0$ より不適。

(ii) $0\leqq b < 1$ のとき

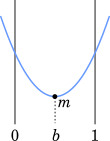
$m < 0$ となる範囲を求めると

$-b^2-\cfrac{4}{3}b+\cfrac{5}{9} < 0$ $9b^2+12b-5 > 0$

$(3b+5)(3b-1) > 0$

$b < -\cfrac{5}{3},\space b > \cfrac{1}{3}$

$0\leqq b < 1$ より $b > \cfrac{1}{3}$

(iii) $b > 1$ のとき

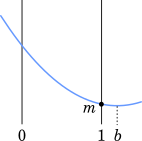
$x=1$ で最小となるので

$f(1)=1-2b-\cfrac{4}{3}b+\cfrac{5}{9}$

$=-\cfrac{10}{3}b+\cfrac{14}{9}$

$m < 0$ となる範囲を求めると

$-\cfrac{10}{3}b+\cfrac{14}{9} < 0$ $30b-14 > 0$

$b > \cfrac{7}{15}$

$b > 1$ より 求める範囲は $b > 1$ となる。

(i)～(iii) より求める範囲は $b > \cfrac{1}{3}$ または $b > 1$ のときだから $b > \cfrac{1}{3}$ である。

次に，$0\leqq x\leqq1$ の範囲で $f(x)$ のグラフと $x$ 軸が異なる 2 点で交わる $b$ の値の範囲を求める。

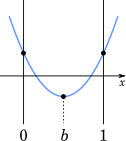
必要な条件は

(i) $0\leqq b\leqq 1$

(ii) $-b^2-\cfrac{4}{3}b+\cfrac{5}{9} < 0$ $b > \cfrac{1}{3}$

(iii) $f(0)\geqq 0$

$-\cfrac{4}{3}b+\cfrac{5}{9}\leqq 0$

$b\leqq\cfrac{5}{12}$

(iv) $f(1)\geqq 0$

$-\cfrac{10}{3}b+\cfrac{14}{9}\geqq0$

$b\leqq\cfrac{7}{15}$

(ii)～(iv) は上で行った計算を用いるとよい。

(i)～(iv) より

$\cfrac{1}{3} < b\leqq\cfrac{5}{12}$