【スマホで読む・わかりやすい】センター数学IA2013本試【解説・正解・問題】

第３問

点 O を中心とする半径 3 の円 O と，点 O を通り，点 P を中心とする半径 $1$ の円 P を考える。円 P の点 O における接線と円 O との交点を A，B とする。また，円 O の周上に，点 B と異なる点 C を，弦 AC が円 P に接するようにとる。弦 AC と円 P の接点を D とする。このとき

AP=$\boxed{\text{ アイ }}$，OD=$\cfrac{\boxed{\text{ ウ }}\sqrt{\boxed{\text{ エオ }}}}{\boxed{\text{ カ }}}$

である。さらに，$\cos$∠OAD$=\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}$ であり，AC=$\cfrac{\boxed{\text{ ケコ }}}{\boxed{\text{ サ }}}$ である。

△ABC の面積は $\cfrac{\boxed{\text{ シスセ }}}{\boxed{\text{ ソタ }}}$ であり，△ABC の内接円の半径は $\cfrac{\boxed{\text{ チ }}}{\boxed{\text{ ツ }}}$ である。

(1)　円 O の周上に，点 E を線分 CE が円 O の直径となるようにとる。 △ABC の内接円の中心を Q とし，△CEA の内接円の中心を R とする。このとき， QR=$\cfrac{\boxed{\text{ テト }}}{\boxed{\text{ ナ }}}$ である。したがって，内接円 Q と内接円 R は $\boxed{\text{ ニ }}$。

$\boxed{\text{ ニ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪　内接する　①　異なる 2 点で交わる
②　外接する　③　共有点を持たない

(2)　AQ=$\cfrac{\boxed{\text{ ヌ }}\sqrt{\boxed{\text{ ネノ }}}}{\boxed{\text{ ハ }}}$ であるから，PQ=$\cfrac{\sqrt{\boxed{\text{ ヒフ }}}}{\boxed{\text{ ヘ }}}$ となる。したがって，$\boxed{\text{ ホ }}$。

$\boxed{\text{ ホ }}$ に当てはまるものを，次の⓪～③ のうちから一つ選べ。

⓪　点 P は内接円 Q の周上にある

①　点 Q は円 P の周上にある

②　点 P は内接円 Q の内部にあり，点 Q は円 P の内部にある

③　点 P は内接円 Q の内部にあり，点 Q は円 P の外部にある

解答・解説

アイ $10$　ウ,エオ,カ $3,10,5$

キ,ク $4,5$　ケコ,サ $24,5$

シスセ,ソタ $216,25$　チ,ツ $6,5$

テト,ナ $12,5$　ニ $2$

ヌ,ネノ,ハ $6,10,5$

ヒフ,ヘ $10,5$　ホ $2$

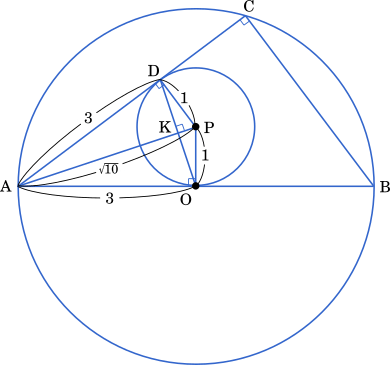
△AOP において，三平方の定理より

$\text{AP}^2=3^2+1^2$

$\text{AP}=\sqrt{10}$

OD と AP の交点を K とおくと，△APD ∽ △DPK だから

DK : DP = $3:\sqrt{10}$

DK : $1$ = $3:\sqrt{10}$

$\sqrt{10}\text{DK} =3$

DK = $\cfrac{3}{\sqrt{10}}=\cfrac{3\sqrt{10}}{10}$

OD = 2DK だから，OD = $\cfrac{6\sqrt{10}}{10}=\cfrac{3\sqrt{10}}{5}$

次に，余弦定理を用いて

$\bigg(\cfrac{3\sqrt{10}}{5}\bigg)^2=3^2+3^2-2\cdot3\cdot3\cos\angle\text{OAD}$

$\cfrac{90}{25}=9+9-18\cos\angle\text{OAD}$

$\cfrac{18}{5}=18-18\cos\angle\text{OAD}$

$\cfrac{1}{5}=1-\cos\angle\text{OAD}$

$\cos\angle\text{OAD}=1-\cfrac{1}{5}=\cfrac{4}{5}$

また，AB は円 O の直径だから，$\angle\text{ACB}=90\degree$ であり

$\cos\angle{\text{OAD}}=\cos\angle\text{BAC}=\cfrac{\text{AC}}{\text{AB}}=\cfrac{\text{AC}}{6}$

$\cos\angle\text{BAC}=\cfrac{\text{AC}}{6}$

$\text{AC}=6\cos\angle\text{BAC}=6\cdot\cfrac{4}{5}=\cfrac{24}{5}$

△ABC の面積を求めると

$\sin^2\angle\text{BAC}+\cos^2\angle\text{BAC}=1$

$\sin^2\angle\text{BAC}=1-\cfrac{16}{25}=\cfrac{9}{25}$

$\sin\angle\text{BAC}=\cfrac{3}{5}$

△ABC = $\cfrac{1}{2}\cdot\text{AB}\cdot\text{AC}\sin\angle\text{BAC}$

$=\cfrac{1}{2}\cdot6\cdot\cfrac{24}{5}\cdot\cfrac{3}{5}$

$=\cfrac{215}{25}$

さらに，三角形の内接円と面積の公式 $S=\cfrac{1}{2}r(a+b+c)$ を用いて
△ABC の内接円の半径を求める。BC を求めると

$\sin\angle\text{BAC}=\cfrac{3}{5}$ より

AB : BC = $5:3$

$6:\text{BC}=5:3$

$5\text{BC}=18$

$\text{BC}=\cfrac{18}{5}$

公式に当てはめると

$\cfrac{216}{25}=\cfrac{1}{2}r\bigg(6+\cfrac{18}{5}+\cfrac{24}{5}\bigg)$

$\cfrac{216}{25}=\cfrac{1}{2}r\cdot\cfrac{72}{5}$

$\cfrac{216}{25}=\cfrac{36}{5}r$

$\cfrac{6}{25}=\cfrac{1}{5}r$

$r=\cfrac{30}{25}=\cfrac{6}{5}$

(1)

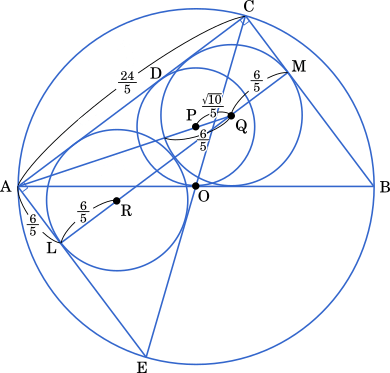
△ACE ≡ △CAB より，円 Q と円 R の内接円は等しい。よって

$\text{QR}=\text{LM}-2\cdot\cfrac{6}{5}$

LM = AC だから

$\text{QR}=\cfrac{24}{5}-\cfrac{12}{5}=\cfrac{12}{5}$

内接円 Q と内接円 R の半径の合計は $2\times\cfrac{6}{5}=\cfrac{12}{5}$ である。したがって，QR と等しいので内接円 Q と内接円 R は外接する。

(2)

△ALQ を考えると

AL = $\cfrac{6}{5}$，LQ = $3\cdot\cfrac{6}{5}=\cfrac{18}{5}$

三平方の定理より

$\bigg(\cfrac{6}{5}\bigg)^2+\bigg(\cfrac{18}{5}\bigg)^2=\text{AQ}^2$

$\text{AQ}^2=\cfrac{36+324}{25}=\cfrac{72}{5}$

$\text{AQ}=\sqrt{\cfrac{72}{5}}=\cfrac{6\sqrt{10}}{5}$

PQ = AQ – AP

$=\cfrac{6\sqrt{10}}{5}-\sqrt{10}$

$=\cfrac{\sqrt{10}}{5}$

ここで，$\cfrac{6}{5}$ と $\cfrac{\sqrt{10}}{5}$ を比べると，おたがいを 2 乗して $\cfrac{36}{25} > \cfrac{10}{25}$ となるので，$\cfrac{6}{5} > \cfrac{\sqrt{10}}{5}$ が成り立つ。

したがって，点 P は内接円 Q の内部にあり，点 Q は円 P の内部にある。