【スマホで読む・わかりやすい】センター数学IA2013本試【解説・正解・問題】

第２問

座標平面上にある点 P は，点 A $(-8,8)$ から出発して，直線 $y=-x$ 上を $x$ 座標が $1$ 秒あたり $2$ 増加するように一定の速さで動く。また，同じ座標平面上にある点 Q は，点 P が A を出発すると同時に原点 O から出発して，直線 $y=10x$ 上を $x$ 座標が $1$ 秒あたり $1$ 増加するように一定の速さで動く。出発してから $t$ 秒後の 2点 P，Q を考える。点 P が O に到達するのは $t=\boxed{\text{ ア }}$ のときである。以下，$0 < t < \boxed{\text{ ア }}$ で考える。

(1)　点 P と $x$ 座標が等しい $x$ 軸上の点を P′，点 Q と $x$ 座標が等しい $x$ 軸上の点を Q′ とおく。△OPP′ と △OQQ′ の面積の和 $S$ を $t$ で表せば

$S=\boxed{\text{ イ }}t^2-\boxed{\text{ ウエ }}t+\boxed{\text{ オカ }}$

となる。これより $0 < t < \boxed{\text{ ア }}$ においては，$t=\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}$ で $S$ は最小値 $\cfrac{\boxed{\text{ ケコサ }}}{\boxed{\text{ シ }}}$ をとる。

次に，$a$ を $0 < a < \boxed{\text{ ア }}-1$ を満たす定数とする。以下，$a\leqq t\leqq a+1$ における $S$ の最小・最大について考える。

(i) $S$ が $t=\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}$ で最小となるような $a$ の値の範囲は

$\cfrac{\boxed{\text{ ス }}}{\boxed{\text{ セ }}} \leqq a \leqq \cfrac{\boxed{\text{ ソ }}}{\boxed{\text{ タ }}}$ である。

(ii) $S$ が $t=a$ で最大となるような $a$ の値の範囲は $0 < a \leqq \cfrac{\boxed{\text{ チ }}}{\boxed{\text{ ツテ }}}$ である。

(2)　3 点 O，P，Q を通る 2 次関数のグラフが関数 $y=2x^2$ のグラフを平行移動したものになるのは，$t=\cfrac{\boxed{\text{ ト }}}{\boxed{\text{ ナ }}}$ のときであり，$x$ 軸方向に $\cfrac{\boxed{\text{ ニヌ }}}{\boxed{\text{ ネ }}}$，$y$ 軸方向に $\cfrac{\boxed{\text{ ノハヒ }}}{\boxed{\text{ フ }}}$ だけ平行移動すればよい。

解答・解説

ア $4$

イ,ウエ,オカ $7,16,32$

キ,ク $8,7$

ケコサ,シ $160,7$

ス,セ $1,7$

ソ,タ $8,7$

チ,ツテ $9,14$

ト,ナ $5,2$

ニヌ,ネ $-5,4$

ノハヒ,フ $-25,8$

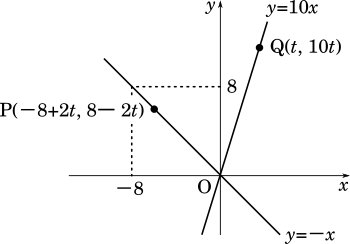
点 P が O に到達するのは $t=4$ のときである。

(1)

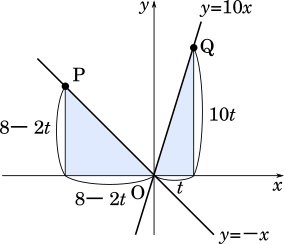
$S=\cfrac{1}{2}(8-2t)^2+\cfrac{1}{2}10t\cdot t$

$=\cfrac{1}{2}\{2(4-t)\}^2+5t^2$

$=\cfrac{1}{2}2^2(4-t)^2+5t^2$

$=2(4-t)^2+5t^2$

$=2(16-8t+t^2)+5t^2$

$=32-16t+2t^2+5t^2$

$=7t^2-16t+32$

平方完成して

$S=7\bigg(t^2-\cfrac{16}{7}t\bigg)+32$

$=7\bigg(t-\cfrac{8}{7}\bigg)^2-\cfrac{64}{7}+32$

$=7\bigg(t-\cfrac{8}{7}\bigg)^2+\cfrac{160}{7}$

 

したがって，$t=\cfrac{8}{7}$ で最小値 $\cfrac{160}{7}$ をとる。

次に，$a$ を

$0 < a < 4-1$

$0 < a < 3$

を満たす定数とする。

(i)

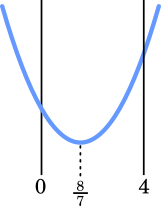
$a\leqq\cfrac{8}{7}$ かつ $\cfrac{8}{7}\leqq a+1$ だから

$\cfrac{1}{7}\leqq a\leqq\cfrac{8}{7}$

(ii)

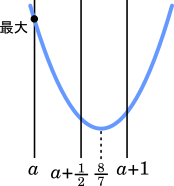
$a+\cfrac{1}{2} \leqq\cfrac{8}{7}$

$a\leqq\cfrac{9}{14}$

これと $0 < a < 3$ を重ねて

$0 < a \leqq\cfrac{9}{14}$

(2)

P$(-8+2t,8-2t)=$P$(2t-8,8-2t)$

Q$(t,10t)$

O$(0,0)$

ここで $y=2x^2$ を平行移動した式を $y=2x^2+kx+\ell$ とする。

O$(0,0)$ を $x,y$ に代入すると

$0=2\cdot 0^2+k\cdot0+\ell$

$\ell=0$

したがって式は

$y=2x^2+kx$

$y=2x\bigg(x+\cfrac{k}{2}\bigg)$

となる。

次に，式に Q$(t,10t)$ を代入すると

$10t=2t\bigg(t+\cfrac{k}{2}\bigg)$

$0 < t$ だから，式を $2t$ で割ると

$5=t+\cfrac{k}{2}$

$\cfrac{k}{2}=5-t$

$k=2(5-t)$

さらに，式に P$(2t-8,8-2t)$ と $k$ の値を代入すると

$8-2t=2(2t-8)(2t-8+5-t)$

$8-2t=4(t-4)(t-3)$

$4-t=2(t-4)(t-3)$

$4-t=2(t^2-7t+12)$

$4-t=2t^2-14t+24$

$2t^2-13t+20=0$

$t=\cfrac{13\pm\sqrt{169-160}}{4}$

$=\cfrac{13\pm\sqrt{9}}{4}$

$=\cfrac{13\pm3}{4}$

$=\cfrac{5}{2},\space 4$

$0 < t < 4$ より $t=\cfrac{5}{2}$

これを $k$ の式に代入して

$k=2\bigg(5-\cfrac{5}{2}\bigg)=5$

これより式は

$y=2x^2+5x$

これを平方完成すると

$y=2\bigg(x^2+\cfrac{5}{2}x\bigg)$

$=2\bigg(x+\cfrac{5}{4}\bigg)^2-\cfrac{25}{8}$

したがって，$x$ 軸方向に $\cfrac{-5}{4}$，$y$ 軸方向に $\cfrac{-25}{8}$ だけ平行移動すればよい。