【スマホで読む・わかりやすい】センター数学IA2012追試【解説・正解・問題】

第3問

点Oを中心とする円Oの二つの弦AB，CDが，円Oの内の点Pにおいて交わっている。
ここで

PA$=1$，PC$=\sqrt{10}$，PD=$\cfrac{\sqrt{10}}{5}$

とし，弦ACの長さは AC=3 とする。

このとき，PB=$\boxed{\text{ ア }}$ であり，∠CAP=$\boxed{\text{ イウ }}\degree$ である。したがって，円Oの直径は $\boxed{\text{ エ }}\sqrt{\boxed{\text{ オ }}}$ である。さらに，$\tan$ ∠PCA=$\cfrac{\boxed{\text{ カ }}}{\boxed{\text{ キ }}}$ となる。

点Pから弦BCに下ろした垂線と弦BCの交点をHとする。このとき，△PHBの外接円の直径は $\boxed{\text{ ク }}$ である。また

∠PHB+∠BDP=$\boxed{\text{ ケコサ }}\degree$

であり，∠BDH=$\boxed{\text{ シス }}\degree$ である。

線分DHの延長と円Oの交点をEとする。∠BDH=$\boxed{\text{ シス }}\degree$ であるので，∠BOE=$\boxed{\text{ セソ }}\degree$ である。したがって，AE=$\boxed{\text{ タ }}\sqrt{\boxed{\text{ チ }}}$ である。

さらに，$\tan$∠PCH=$\cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ テ }}}$ となる。

次の⓪～③のうち，△AEDと相似な三角形は$\boxed{\text{ ト }}$と$\boxed{\text{ ナ }}$ である。ただし，$\boxed{\text{ ト }}$ と $\boxed{\text{ ナ }}$ の解答の順序は問わない。

⓪ △BCD　① △PCA　② △PCH　③ △HEO

解答・解説

ア $2$

イウ $90$

エ $3$

オ $\sqrt{2}$

カ $1$

キ $3$

ク $2$

ケコサ $180$

シス $45$

セソ $90$

タ $3$

チ $2$

ツ $1$

テ $2$

ト，ナ　$1,3$ または $3,1$

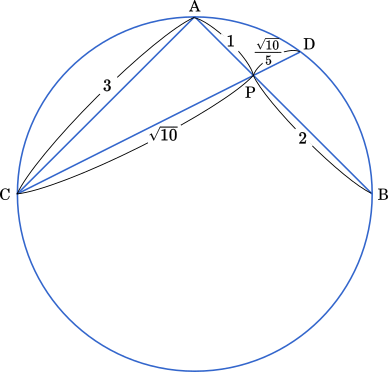
方べきの定理より

$\text{PA}\cdot\text{PB}=\text{PC}\cdot\text{PD}\\1\times\text{PB}=\sqrt{10}\cdot\cfrac{\sqrt{10}}{5}\\\text{PB}=2$

余弦定理を用いて

$(\sqrt{10})^2=1^2+3^2-2\cdot 1\cdot 3\cdot\cos\angle\text{CAP}\\10=10-6\cos\angle\text{CAP}\\\cos\angle\text{CAP}=0\\\angle\text{CAP}=90\degree$

よって，BC は直径である。△ABC は辺の比が $1:1:\sqrt{2}$ の直角二等辺三角形だから，$\text{BC}=3\sqrt{2}$

また，$\tan\angle{\text{PCA}}=\cfrac{1}{3}$

△PHB の外接円の直径を考えると $\angle\text{PHB}=90\degree$ より PB が円の直径となる。よって直径は $2$

また，△BCD で考えると BC は直径だから ∠CDB は $90\degree$ である。したがって，∠BDP$=90\degree$

∠PHB + ∠BDP $=90\degree+90\degree=180\degree$

円周上の 4 点からなる四角形の向かい合う角の和は $180\degree$ であることから，P,H,B,D は同一円周上にあることが分かる。

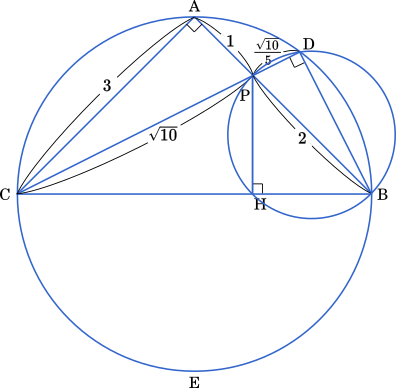
次に，△ABC は直角二等辺三角形だから ∠ABC = ∠ PBH = $45\degree$ である。円周角の定理より

∠PBH = ∠PDH = $45\degree$

したがって，∠BDH = $45\degree$

また，円 O で考えると ∠BOE は ∠BDE の中心角だから ∠BOE = $90\degree$

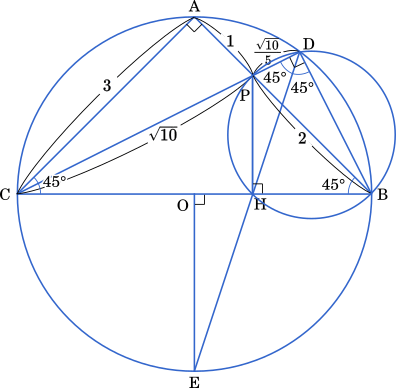
さらに AE を求める。円周角の定理より ∠BDE = ∠BAE = $45\degree$

このとき △ABC は直角二等辺三角形だから AE は BC の中点，つまり中心 O を通る。したがって，AE は円O の直径であり，AE = $3\sqrt{2}$

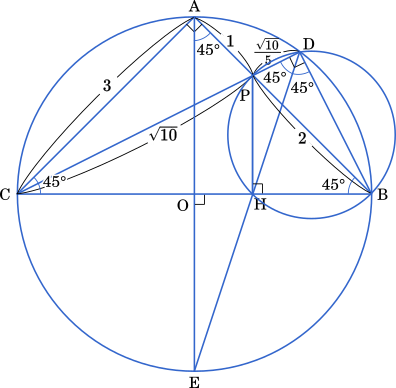
次に $\tan$ ∠PCH を考える。∠PCH = ∠DCB であることと，公式 $1+\tan\theta=\cfrac{1}{\cos^2\theta}$ を用いて

$\cos$ ∠PCH = $\cfrac{\sqrt{10}+\cfrac{\sqrt{10}}{5}}{3\sqrt{2}}$

分母・分子を 5 倍して

$=\cfrac{5\sqrt{10}+\sqrt{10}}{15\sqrt{2}}=\cfrac{6\sqrt{10}}{15\sqrt{2}}\\=\cfrac{2\sqrt{10}}{5\sqrt{2}}=\cfrac{2\sqrt{20}}{10}\\=\cfrac{4\sqrt{5}}{10}=\cfrac{2\sqrt{5}}{5}$

$\cfrac{1}{\cos^2\angle\text{PCH}}=\cfrac{1}{\bigg(\cfrac{2\sqrt{5}}{5}\bigg)^2}\\=\cfrac{1}{\cfrac{20}{25}}=\cfrac{1}{\cfrac{4}{5}}=\cfrac{5}{4}$

$1+\tan^2\angle\text{PCH}=\cfrac{5}{4}\\\tan^2\angle\text{PCH}=\cfrac{1}{4}\\\tan\angle\text{PCH}=\cfrac{1}{2}$

さらに △AED と相似な三角形を考える。

△AED は AE が直径であることから，∠ADE = $90\degree$ である。

△AED と △PCA は 円周角の定理より ∠AED = ∠ACD であり，∠ADE = ∠PAC = $90\degree$ であるから，△AED ∽ △PCA である。

また，△AED と △HEO は ∠AED = ∠OEH であり，∠ADE = ∠EOH = $90\degree$ であるから，△AED ∽ △HEO である。