【スマホで読む・わかりやすい】センター数学IA2012追試【解説・正解・問題】

第２問

$a$ を $0$ でない定数とするとき，$x$ の2次関数

$y=ax^2-(6-2a)x+4\cdots$①

のグラフを $G$ とする。グラフ $G$ が $x$ 軸と共有点をもたない $a$ の値の範囲は

$\boxed{\text{ ア }} < a < \boxed{\text{ イ }}\cdots$②

である。

以下，$a$ は②の範囲にあるとする。

$G$ の頂点の座標は

$\bigg(\cfrac{\boxed{\text{ ウ }}}{a}-\boxed{\text{ エ }},\boxed{\text{ オ }}a+\boxed{\text{ カキ }}-\cfrac{\boxed{\text{ ク }}}{a}\bigg)$

である。ここで，$k=\cfrac{\boxed{\text{ ウ }}}{a}-\boxed{\text{ エ }}$ とおけば，②より

$\cfrac{\boxed{\text{ ケ }}}{\boxed{\text{ コ }}} < \cfrac{\boxed{\text{ ウ }}}{a} < \boxed{\text{ サ }}$

なので，この $k$ の値の範囲は

$\cfrac{\boxed{\text{ シス }}}{\boxed{\text{ セ }}} < k < \boxed{\text{ ソ }}$
である。

(1)　関数①の $-1\leqq x \leqq 0$ における最小値を $m$ とする。

$x=k$ で 最小値　$m=\boxed{\text{ オ }}a+\boxed{\text{ カキ }}-\cfrac{ク}{a}$

をとるのは，$\boxed{\text{ タ }}\leqq a <\boxed{\text{ イ }}$ のときである。

一方，$\boxed{\text{ ア }} < a\leqq\boxed{\text{ タ }}$ のときは $x=\boxed{\text{ チ }}$ で 最小値 $m=\boxed{\text{ ツ }}$ をとる。 (2)　関数①の $-1\leqq x\leqq 0$ における最大値を $M$ とする。 $M>4$ となるとき

$x=\boxed{\text{ テト }}$ で 最大値 $M=\boxed{\text{ ナ }}a+\boxed{\text{ ニヌ }}$

をとる。ただし，$M>4$ となる $a$ の値の範囲は，$\boxed{\text{ ア }} < a < \boxed{\text{ ネ }}$

である。

解答・解説

ア,イ $1$,$9$

ウ $3$

エ $1$

オ $-$

カキ $10$

ク $9$

ケ $1$

コ $3$

サ $3$

シス $-2$

セ $3$

ソ $2$

タ $3$

チ $0$

ツ $4$

テト $-1$

ナ $-$

ニヌ $10$

ネ $6$

式を $f(x)=ax^2-(6-2a)x+4$ とおく。

グラフが $x$ 軸と共有点ををもたないとき，判別式 $D < 0$ が成り立つ。

$\cfrac{D}{4}=(3-a)^2-4a < 0$

$9-6a+a^2-4a < 0$

$a^2-10a+9 < 0$

$(a-1)(a-9) < 0$

$1 < a < 9$

次に頂点を求めるには式を平方完成するとよい。

$f(x)=ax^2-(6-2a)x+4\\=a\bigg(x^2-\cfrac{6-2a}{a}x\bigg)+4\\=a\bigg(x-\cfrac{3-a}{2}\bigg)^2-a\bigg(\cfrac{3-a}{a}\bigg)^2+4\\=a\bigg(x-\cfrac{3}{3}+1\bigg)^2-\cfrac{9-6a+a^2}{a}+4\\=a\bigg(x-\cfrac{3}{a}+1\bigg)^2-a+10-\cfrac{9}{a}$

頂点の座標は $\bigg(\cfrac{3}{a}-1,-a+10-\cfrac{9}{a}\bigg)$

$k=\cfrac{3}{a}-1$ とおけば，②より

$1 < a < 9$

ここで $2 < 3$ は $\cfrac{1}{2} > \cfrac{1}{3}$ となるように逆数をとると不等号の向きが逆になることに注意して

$\cfrac{1}{9} < \cfrac{1}{a} < 1\\\cfrac{1}{3} < \cfrac{3}{a} < 3\\-\cfrac{2}{3} < \cfrac{3}{a}-1 < 2\\-\cfrac{2}{3} < k <2$

(1)

$k$ は頂点の $x$ 座標であるから，頂点で最小値をとるとき，頂点の $x$ 座標は $-1$ と $0$ の間にある。

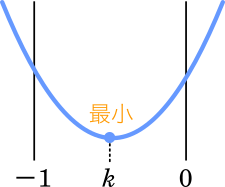
$-1\leqq k \leqq 0\\-1\leqq\cfrac{3}{a}-1\leqq 0\\0\leqq\cfrac{3}{a}\leqq 1$
ここで不等式を 2 つに分けるとよい。
$0\leqq\cfrac{3}{a}$
逆数をとって
$0\geqq\cfrac{a}{3}\\0\geqq a$
また
$\cfrac{3}{a}\leqq 1\\\cfrac{a}{3}\geqq 1\\a\geqq 3$
これと $1 < a < 9$ を重ねて
$3\leqq a < 9$

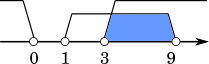
一方，$1 < a\leqq 3$ のときを考える。不等式を変形して　$k$ の範囲を求めるとよい

$1 < a\leqq 3$

逆数をとって

$\cfrac{1}{3}\leqq\cfrac{1}{a} < 1\\1\leqq\cfrac{3}{a} < 3\\0\leqq\cfrac{3}{a}-1 < 2\\0\leqq k < 2$

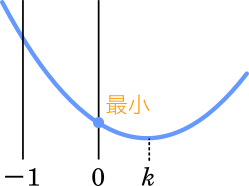
したがって，$x=0$ で最小となる。これを $f(x)$ に代入して

$f(0)=4$ だから，最小値 $m=4$

(2)

最大値の場所は頂点の $x$ 座標によって変わるので，場合分けをする。

(i) $-1\leqq k < -\cfrac{1}{2}$ のとき $x=0$ で最大。 図 $f(0)=4$ だから，最大値 $M=4$ $M > 4$ より，不適。

(ii) $-\cfrac{1}{2}\leqq k\leqq 0$ のとき $x=-1$ で最大
$f(-1)=-a+10$

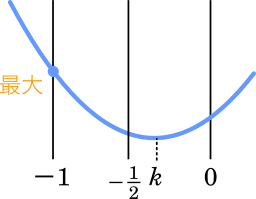
$M > 4$ より $-a+10 > 4$ となる。式を整理して

$-a > -6\\a < 6$

これと，$1 < a < 9$ を重ねて

$1 < a < 6$