【スマホで読む・わかりやすい】センター数学IA2012本試【解説・正解・問題】

第3問

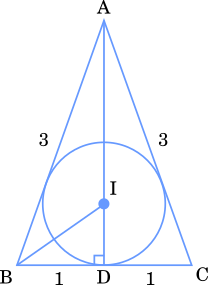
△ABC において，AB=AC=$3$，BC=$2$ であるとき

$\cos$∠ABC= $\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}$，$\sin$∠ABC=$\cfrac{\boxed{\text{ ウ }}\sqrt{\boxed{\text{ エ }}}}{\boxed{\text{ オ }}}$

であり，△ABC の面積は $\boxed{\text{ カ }}\sqrt{\boxed{\text{ キ }}}$，△ABC の内接円I の半径は $\cfrac{\sqrt{\boxed{\text{ ク }}}}{\boxed{\text{ ケ }}}$ である。

また円 I の中心から点 B までの距離は $\cfrac{\sqrt{\boxed{\text{ コ }}}}{\boxed{\text{ サ }}}$ である。

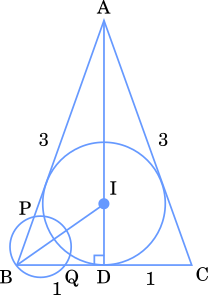
(1)　辺 AB 上の点 P と辺 BC 上の点 Q を， BP=BQ かつ PQ=$\cfrac{2}{3}$ となるようにとる。このとき，△PBQ の外接円 O の直径は $\cfrac{\sqrt{\boxed{\text{ シ }}}}{\boxed{\text{ ス }}}$ であり，円 I と円 O は $\boxed{\text{ セ }}$。ただし，$\boxed{\text{ セ }}$ には次の⓪～④から当てはまるものを一つ選べ。

⓪ 重なる（一致する）　① 内接する　② 外接する
③ 異なる2点で交わる　④ 共有点をもたない

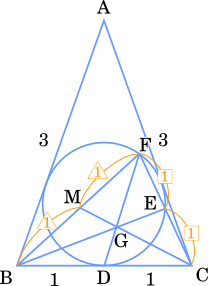
(2)　円 I 上に点 E と点 F を，3 点 C，E，F が一直線上にこの順に並び，かつ，CF=$\sqrt{2}$ となるようにとる。このとき
CE=$\cfrac{\sqrt{\boxed{\text{ ソ }}}}{\boxed{\text{ タ }}}$，$\cfrac{\text{EF}}{\text{CE}}=\boxed{\text{ チ }}$
である。
さらに，円 I と辺 BC との接点を D ， 線分 BE と線分 DF との交点を G，線分 CG の延長と線分 BF との交点を M とする。このとき，$\cfrac{\text{GM}}{\text{CG}}=\cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ テ }}}$ である。

正解と解説

$\cfrac{\text{ア}}{\text{イ}}$ $\cfrac{1}{3}$

$\cfrac{\text{ウ}\sqrt{\text{エ}}}{\text{オ}}$ $\cfrac{2\sqrt{2}}{3}$

カ$\sqrt{\text{キ}}$ $2\sqrt{2}$

$\cfrac{\sqrt{\text{ク}}}{\text{ケ}}$ $\cfrac{\sqrt{2}}{2}$

$\cfrac{\sqrt{\text{コ}}}{\text{サ}}$ $\cfrac{\sqrt{6}}{2}$

$\cfrac{\sqrt{\text{シ}}}{\text{ス}}$ $\cfrac{\sqrt{2}}{2}$

セ $3$

$\cfrac{\sqrt{\text{ソ}}}{\text{タ}}$ $\cfrac{\sqrt{2}}{2}$

チ $1$

$\cfrac{\text{ツ}}{\text{テ}}$ $\cfrac{1}{2}$

余弦定理より
$3^2=3^2+2^2-2\cdot3\cdot2\cdot\cos$∠ABC
$\cos$∠ABC$=\cfrac{1}{3}$

公式 $\sin^2 x+\cos^2 x=1$ より
$\sin^2$ B$+\Big(\cfrac{1}{3}\Big)^2=1$
$\sin^2$ B$=\cfrac{8}{9}$
△ABCは鋭角三角形だから
$\sin$ B$=\cfrac{2\sqrt{2}}{3}$

次に△ABCの面積は
$\cfrac{1}{2}\cdot3\cdot2\cdot\cfrac{2\sqrt{2}}{3}=2\sqrt{2}$

次に△ABCの内接円 I の半径を求める。円の中心を I とおき，BC との接点を D とする。△ABC は二等辺三角形より AD⊥BC かつ 点 D は BCの中点である。
△ABD において，三平方の定理より
$1^2+\text{AD}^2=3^2$
$\text{AD}^2=8$
AD$=2\sqrt{2}$
また，AO : OD$=3:1$ より
OD$=2\sqrt{2}\times\cfrac{1}{4}=\cfrac{\sqrt{2}}{2}$

△BDI において，三平方の定理より
$1^2+\Big(\cfrac{\sqrt{2}}{2}\Big)=\text{BI}^2$
$\text{BI}^2=1+\cfrac{1}{2}=\cfrac{3}{2}$
$\text{BI}=\cfrac{\sqrt{6}}{2}$

(1) △PBQ の外接円 O の直径を求める。
正弦定理より
$\cfrac{\cfrac{2}{3}}{\sin\angle\text{PBQ}}=2R$
$2R=\cfrac{\cfrac{2}{3}}{\cfrac{2\sqrt{2}}{3}}$
$=\cfrac{2}{2\sqrt{2}}$
$=\cfrac{\sqrt{2}}{2}$
次に円 I と円 O の関係を考える。
円 I の半径＋円 O の直径
$\cfrac{\sqrt{2}}{2}+\cfrac{\sqrt{2}}{2}=\sqrt{2}$
また BI$=\cfrac{\sqrt{6}}{2}$ より， $\cfrac{\sqrt{6}}{2} < \sqrt{2}$ だから，円 I と円 O は異なる 2 点で交わる。

(2)

方べきの定理より
$\text{CE}\cdot\text{CF}={\text{CD}}^2$
$\text{CE}\cdot\sqrt{2}=1$
$\text{CE}=\cfrac{\sqrt{2}}{2}$
$\cfrac{\text{EF}}{\text{CE}}=\cfrac{\sqrt{2}-\cfrac{\sqrt{2}}{2}}{\cfrac{\sqrt{2}}{2}}$
分母と分子に $\sqrt{2}$ をかけると
$=\cfrac{2-1}{1}=1$
したがって，CE : EF = $1:1$

次に，$\cfrac{\text{MG}}{\text{GC}}$ を求める。
チェバの定理より
$\cfrac{\text{FM}}{\text{MB}}\times\cfrac{1}{1}\times\cfrac{1}{1}=1$
したがって，FM : MB $=1:1$

また，メネラウスの定理より
$\cfrac{\text{CE}}{\text{EF}}\times\cfrac{\text{FB}}{\text{BM}}\times\cfrac{\text{MG}}{\text{GC}}=1$
$\cfrac{1}{1}\times\cfrac{2}{1}\times\cfrac{\text{MG}}{\text{GC}}=1$
$\cfrac{\text{MG}}{\text{GC}}=\cfrac{1}{2}$