【スマホで読む・わかりやすい】センター数学IA2012本試【解説・正解・問題】

第2問

$a$，$b$ を定数として2次関数
$y=-x^2+(2a+4)x+b\cdots$①
について考える。関数①のグラフ $G$ の頂点の座標は
$(a+\boxed{\text{ ア }},a^2+\boxed{\text{ イ }}a+b+\boxed{\text{ ウ }})$
である。以下，この頂点が直線 $y=-4x-1$ 上にあるとする。このとき，
$b=-a^2-\boxed{\text{ エ }}a-\boxed{\text{ オカ }}$
である。

(1)　グラフ $G$ が $x$ 軸と異なる2点で交わるような $a$ の値の範囲は
$a < \cfrac{\boxed{\text{ キク }}}{\boxed{\text{ ケ }}}$
である。また，$G$ が $x$ 軸の正の部分と負の部分の両方で交わるような $a$ の値の範囲は
$-\boxed{\text{ コ }}-\sqrt{\boxed{\text{ サ }}} < a < -\boxed{\text{ コ }}+\sqrt{\boxed{\text{ サ }}}$
である。

(2)　関数①の $0 \leqq x \leqq 4$ における最小値が $-22$ となるのは
$a=\boxed{\text{ シス }}$ または $a=\boxed{\text{ セ }}$
のときである。また $a=\boxed{\text{ セ }}$ のとき，関数①の $0\leqq x \leqq 4$ における最大値は $\boxed{\text{ ソタチ }}$ である。
一方，$a=\boxed{\text{ シス }}$ のときの①のグラフを $x$ 軸方向に$\boxed{\text{ ツ }}$，$y$ 軸方向に $\boxed{\text{ テトナ }}$ だけ平行移動すると， $a=\boxed{\text{ セ }}$ のときのグラフと一致する。

正解と解説

$(a+$ア,$a^2+$イ$a+b+$ウ$)$ $(a+2,a^2+4a+b+4)$

$-a^2-$エ$a-$オカ　$-a^2-8a-13$

$\cfrac{\text{キク}}{ケ}$ $\cfrac{-9}{4}$

$-$コ$-\sqrt{\text{サ}}$ $-4-\sqrt{3}$

シス $-3$

セ $1$

ソタチ $-13$

ツ $4$

テトナ $-16$

$G:y=-x^2+(2a+4)x+b\cdots$①

平方完成すると
$y=-\{x^2-(2a+4)x\}+b$
$=-\{x-(a+2)\}^2+(a+2)^2+b$
$=-(x-a-2)^2+a^2+4a+b+4$
したがって頂点の座標は
$(a+2,a^2+4a+b+4)$
これを $y=-4x-1$ に代入すると
$a^2+4a+b+4=-4(a+2)-1$
$a^2+4a+b+4=-4a-8-1$
$b=-a^2-8a-13$

(1)　$G$ が $x$ 軸と異なる 2 点で交わるとき，頂点の $y$ 座標は正の値になる。

$-4x-1 > 0$
頂点の $x$ 座標を代入して
$-4(a+2)-1 > 0$
$-4a-9 > 0$
$a < \cfrac{-9}{4}$
つぎに，$G$ が $x$ 軸の正の部分と負の部分の両方で交わるときを考える。まず①に $b=-a^2-8a-13$ を代入して
$f(x)=-x^2+(2a+4)x-a^2-8a-13$

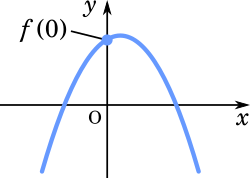
上の図より，$f(0) > 0$ が成り立つことが分かる。
したがって
$f(0)=-a^2-8a-13 > 0$
$-a^2-8a-13=0$ とおくと
$a=-4\pm\sqrt{16-13}$
$=-4\pm\sqrt{3}$
したがって $-4-\sqrt{3} < a < -4+\sqrt{3}$

(2) 頂点の $x$ 座標によって場合分けをするとよい。
(i) $a+2 < 2$ ⇔ $a < 0$ のとき

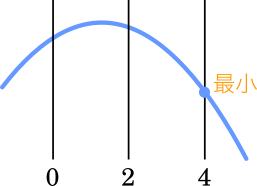
図より，$f(4)$ で最小となる。
$f(4)=-16+(2a+4)\times 4-a^2-8a-13=-22$
$-a^2-13=-22$
$a^2=9$
$a=\pm 3$
$a < 0$ より $a=-3$

(ii) $a\geqq 0$ のとき

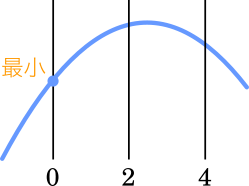
図より，$f(0)$ で最小となる。
$f(0)=-a^2-8a-13=-22$
$a^2+8a-9=0$
$(a+9)(a-1)=0$
$a=1,-9$
$a\geqq 0$ より $a=1$
したがって，最小値が $-22$ となるのは
$a=-3$ または $a=1$ のときである。

また，$a=1$ のとき
頂点の $x$ 座標は $a+2=1+2=3$ となる

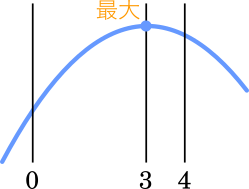
図より，頂点で最大となるので
$y=-4x-1$ に $x=3$ を代入して
$y=-4\times 3-1=-13$
一方，$a=-3$ のとき，頂点の $x$ 座標は $a+2=-3+2=-1$
また，頂点は $y=-4x-1$ 上にあるので，$x$ が $-1$ から $3$ に変化するとき $x$ の変化量は $4$ であり，$y$ の変化量は $-4\times 4=-16$ である。したがって，$x$ 軸に $4$，$y$ 軸方向に $-16$ だけ平行移動すればよい。