経済格差は努力の結果だけではない 平等な立場でも格差が起こることを示す実験
私たちが住む資本主義社会には豊かな人々と貧しい人々がいます。誰もがなぜ個人の間に経済格差が起こるかという疑問を抱くことでしょう。そのとき私たちはその原因は個人の努力の差であると教えられます。しかし、本当にそうなのか?という疑問を投げかける思考実験があります。今回は実際にそれをシミュレーションしてみようというお話です。
この思考実験は誰でも手軽に行うことができます。とは言え、多少プログラミングの知識が必要です。今回使用するのはExcel VBAです。
お金を交換する実験方法
実験の手順を説明しましょう。
まず100人の人間がいます。この人々は初めにそれぞれ 1000円の所持金を持っています。そして人々は他の99人の誰かにランダムに1円を支払います。この操作を何度も繰り返していくのです。実験ではこの作業を 10万 回繰り返しました。
人々は 1 円を支払いますが、同時に他の 99 人から 1 円を受け取る可能性があります。従ってすべての人々の所持金の合計は変化しません。その合計は1000×100=10万円 となります。
ランダムにお金を交換しているので、普通に考えればそれぞれが所持する金額は全員同じ 1000 円に落ち着くはずです。
しかし、実際にこのプロセスを実行すると、まったく異なった結果になります。
参考までに、実験に用いた VBA のソースを示しておきます。
Sub テキストボックス_Click()
Dim 所持金(99)
Dim 支払う相手(99)
Dim a
Dim b
Dim c
Randomize '乱数の初期化
For i = 0 To 99
所持金(i) = 1000 '全員の所持金の初期値を1000に設定
Next i
For y = 0 To 99999
For i = 0 To 99
支払う相手(i) = i '初期値として支払う相手を1~99とする
Next i
'支払う相手をランダムシャッフルする
'2人をランダムに選び支払う相手をお互いに入れ替える
'この作業を1000回繰り返す
For i = 0 To 1000
a = Int(100 * Rnd) '0~99で乱数発生
b = Int(100 * Rnd) '0~99で乱数発生
c = a
支払う相手(a) = 支払う相手(b)
支払う相手(b) = c 'この作業によってaとbの値が入れ替わる
Next i
For i = 0 To 99
所持金(i) = 所持金(i) - 1
所持金(支払う相手(i)) = 所持金(支払う相手(i)) + 1
Next i
Next y
'結果を出力
For x = 0 To 99
ActiveSheet.Cells(5, x + 1).Value = 所持金(x)
Next x
End Sub
実験を繰り返した結果の 4 パターンを以下に示します。
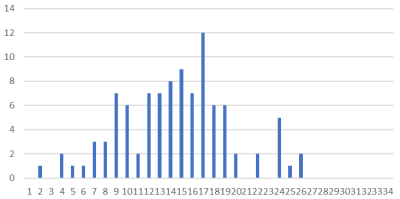
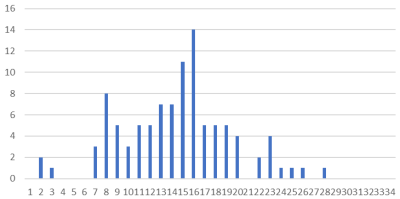
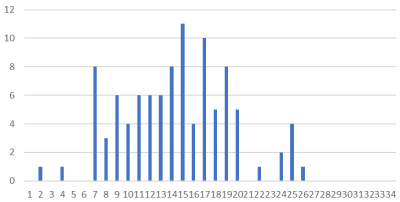
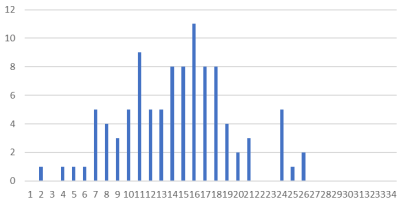
グラフは度数分布表です。
グラフの読み方ですが、横軸は 100 円単位となっていて、1は-399から-300 円までの人数を示しています。また、14が901~1000円、15が1001~1100円を示しています。縦軸は人数を表します。
ランダムに交換しても格差は起こる
実験の結果は実に奇妙です。ランダムにお金を交換しているなら、全ての人の所持金は最終的に同じ 1000 円に収まりそうです。横軸の 14 は 901~1000 円、15 は 1001~1100 円を示しています。しかし実際にはそうではなく、大きな格差が生じています。この度数分布表では 1 から 4 は それぞれ -399円~300円、-299~200円、-199~100円、99~0円に対応していて、グラフを見ると 10万回の経済行為で所持金がマイナスになっている人々が一定数出現していることが分かります。
一方でグラフの横軸は 25 が 2000~2099円、26 が 2100~2199 円に当たり、財産を 2 倍に増やした人々がわずかながら存在していることが分かります。
そしてそれぞれのグラフの形を見てみると、これらが正規分布を示していることに気づくでしょう。
ランダムにお金を交換したときになぜその結果が正規分布を示すのかという問いは、数学者の手ほどきを受けなければならない事項かもしれませんが、この現象は単なる偶然ではないようです。
社会全体としては豊かになる不思議
また、ここでもう一つ疑問点です。
グラフを見ると、正規分布の山がやや右に寄っているような気がします。そこで、中央値を求めてみました。
実験を 4 回繰り返した結果は 1048, 1011,1009,1035 でした。わずかですが、中央値はもともとの 1000 よりも増えています。
これもまた奇妙な結果と言えます。実際にVBA を実行して確かめてほしいのですが、この実験を何度繰り返しても中央値は1000よりも大きな値を示し、マイナスになることはありません。
これが意味することは、平等な経済活動を行ったとしても一部の人々は貧しくなり、その一方で市場全体としては豊かになった人々がそれを上回るということです。
この状況において社会調査を行った場合、景気が悪いと考える人と良いと考える人の割合は、良くなっていると答える人の方が悪くなっていると答える人を上回ることを示唆しています。しかし、経済全体として貨幣の量は同じであることに注意して下さい。
この実験結果が私たちの経済についてどのような意味を持つのかについては、まだほとんど分かっていません。しかし実験の結果は経済格差の問題がその人の努力の結果であるという認識は誤りであるかもしれないことを示唆しているのです。
SNSでシェア