空間ベクトルと四面体の体積の求め方(東京都立大2018理系第3問)

空間において，点 O を中心とする半径 1 の球面上に 3 点 A，B，C をとる。ただし，4 点 O，A，B，C は同一平面上にはないとする。3 点 O，A，C が定める平面 OAC と平面 OAB のなす角を $\alpha$ とし，平面 OAB と平面 OBC のなす角を $\beta$ とし，さらに平面 OBC と平面 OAC のなす角を $\gamma$ とする。また，$a=\angle\text{BOC}$，$b=\angle\text{COA}$，$c=\angle\text{AOB}$ とする。以下の問いに答えなさい。（東京都立大2018）

(1) 平面 OAB 上に点 P を，直線 CP が平面 OAB と直交するようにとる。また，直線 OA 上に点 F を，直線 PF が直線 OA と直交するようにとる。直線 OA と直線 CF が直交することを示しなさい。

(2) 四面体 OABC の体積を $\sin b$，$\sin c$，および $\sin\alpha$ を用いて表しなさい。

(3) 以下の等式が成り立つことを示しなさい。
$\cfrac{\sin\alpha}{\sin a}=\cfrac{\sin\beta}{\sin b}=\cfrac{\sin\gamma}{\sin c}$

内積を利用する

(1)から始めます。

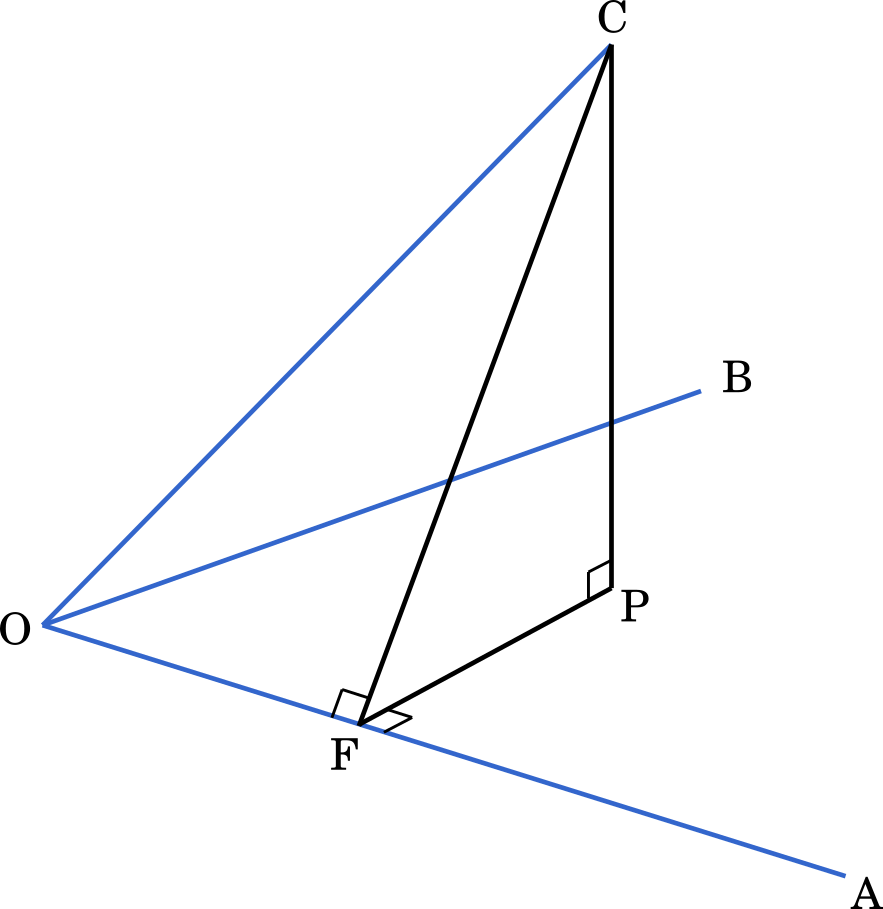
今回の問題では A，B，C が球面上にあるというのはあまり関係ありません。OA=OB=OC=1 が成り立つことだけ，あとで利用します。
いったん，図を描いてみて，垂直であることから内積が 0 になる関係を式にしていきましょう。
$\text{OA}\perp\text{CP}$ より
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CP}}=0$
$\overrightarrow{\text{OA}}(\overrightarrow{\text{OP}}-\overrightarrow{\text{OC}})=0$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=0$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OP}}=\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}$ ・・・①
また，$\text{OA}\perp\text{PF}$ より 
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{PF}}=0$
$\overrightarrow{\text{OA}}(\overrightarrow{\text{OF}}-\overrightarrow{\text{OP}})=0$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OF}}-\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OP}}=0$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OF}}=\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OP}}$　・・・②
①，②より
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OF}}$ ・・・③
ここで，点 F が OA 上の点であることを思い出しましょう。内積の公式より
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OF}}=|\overrightarrow{\text{OA}}||\overrightarrow{\text{OF}}|\cos\theta$
となりますが，$\theta$ は 0 だから
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OF}}=0$ ・・・④
です。
向きが同じベクトルどうしの内積は 0 になる。
③に代入して
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=0$　・・・⑤
問題文から分かることが整理できたので，あとは，$\text{OA}\perp\text{CF}$ を示しましょう。
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CF}}$
$=\overrightarrow{\text{OA}}(\overrightarrow{\text{OF}}-\overrightarrow{\text{OC}})$
$=\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OF}}-\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}$
④，⑤より
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CF}}=0$
（証明終わり）

四面体の体積を求める

(2)に進みます。

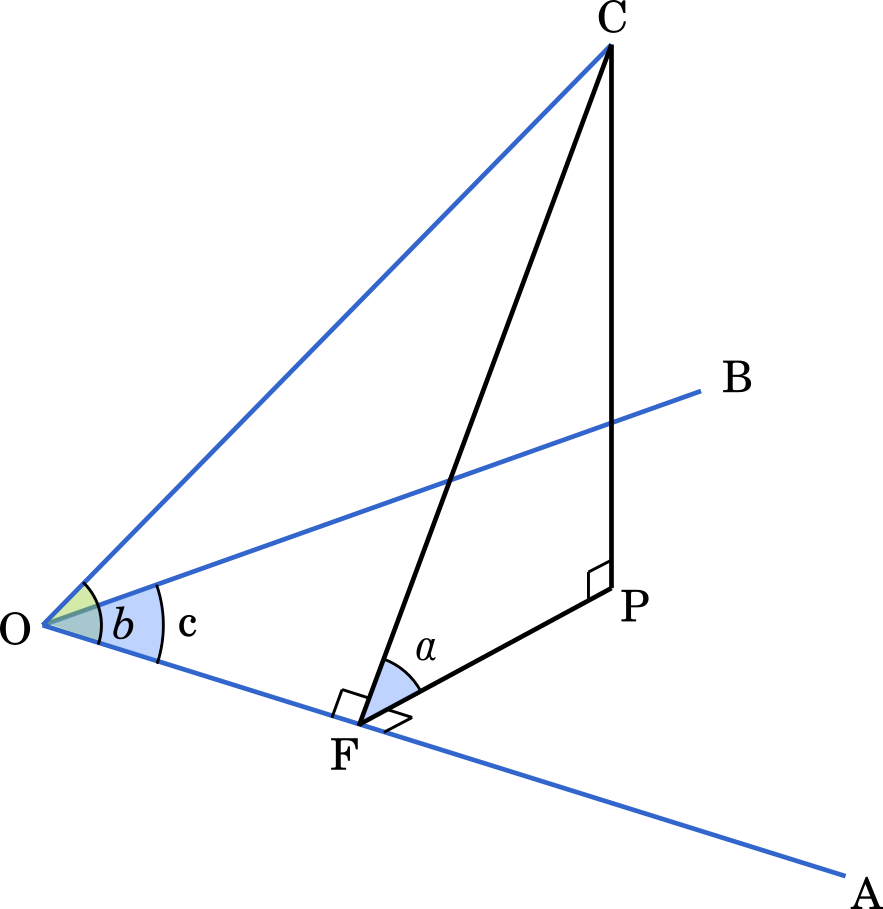
錐体の体積は，公式から
$V=\cfrac{1}{3}\times(\textsf{底面積})\times(\textsf{高さ})$
で求められます。そこで，底面積と高さを考えていきます。
△OAB を底辺とすると，面積は公式を用いて
$S=\cfrac{1}{2}\times\text{OA}\times\text{OB}\times\sin\angle\text{AOB}$ 
となります。
$S=\cfrac{1}{2}\cdot1\cdot1\cdot\sin c=\cfrac{1}{2}\sin c$
次に高さを求めます。

ただし，いきなり CP の長さを出すことはできません。$\sin$ をうまく使って求めてみます。

よって
$\text{CP}=\text{CF}\sin\alpha$
CF を求めます。
$\text{CF}=\text{OC}\sin b$
$\text{OC}=1$ だから
$\text{CP}=\sin b\sin\alpha$
となるのです。
$V=\cfrac{1}{3}\cdot\cfrac{1}{2}\sin c\sin b\sin \alpha$
$=\cfrac{1}{6}\sin b\sin c\sin\alpha$
（答え）

等式の証明

(3)に進みます。
(1)では OA 上に点 F を作りましたが，OB や OC 上に点を作っても同じ手順で体積を出すことができることは容易に想像できると思います。
これには対称性があって，$\sin\alpha$ のとき，残りの $\sin$ は $b$ と $c$ になるので，$\sin\beta$ のとき，残りの $\sin$ は $a$ と $c$ となります。
よって
$\cfrac{1}{6}\sin b\sin c\sin\alpha=\cfrac{1}{6}\sin a\sin c\sin\beta=\cfrac{1}{6}\sin a\sin b\sin\gamma$
$\sin b\sin c\sin\alpha=\sin a\sin c\sin\beta=\sin a\sin b\sin\gamma$
辺々を $\sin a\sin b\sin c$ で割ると
$\cfrac{\sin\alpha}{\sin a}=\cfrac{\sin\beta}{\sin b}=\cfrac{\sin\gamma}{\sin c}$
（証明終わり）