ベクトル方程式と単位ベクトルを用いて座標を求める(東京都立大2017理学部第2問)

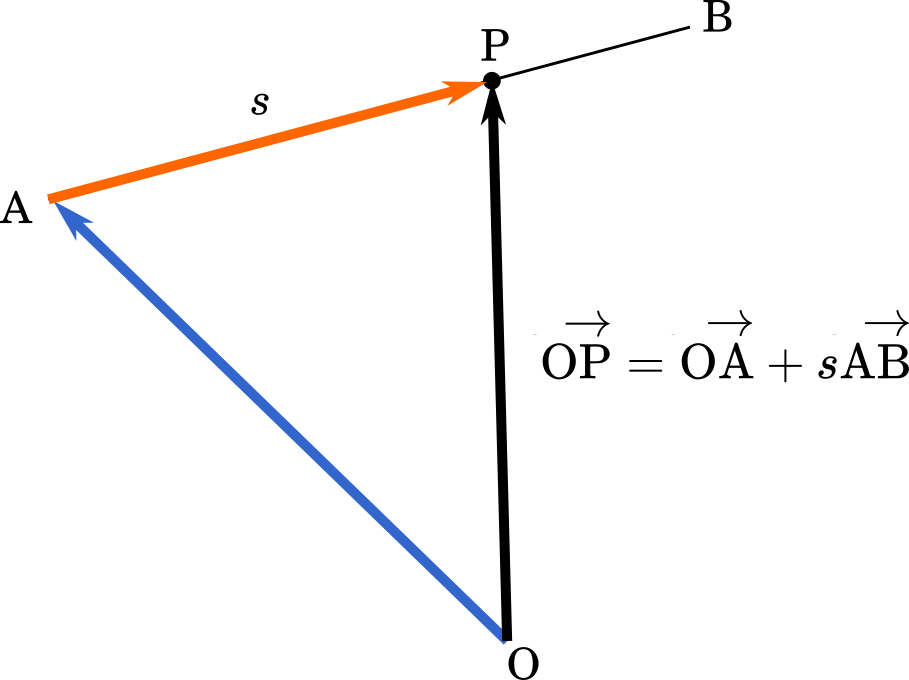
まず,$\overrightarrow{\text{OP}}=\overrightarrow{\text{OA}}+\overrightarrow{\text{AP}}$ とします。AP は AB に平行なので,$\overrightarrow{\text{AB}}$ を $s$ 倍したものが $\overrightarrow{\text{AP}}$ であるとします。
$\overrightarrow{\text{OP}}=\overrightarrow{\text{OA}}+s\overrightarrow{\text{AB}}$
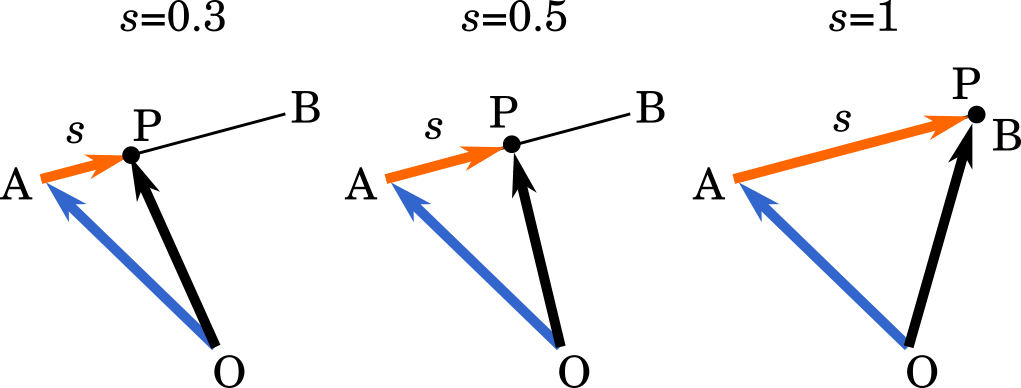





演習問題
座標空間に 4 点
A$(-3,0,2)$,B$(1,4,0)$,C$(0,3,5)$,D$(2,2,7)$
をとる。A,B を通る直線を $\ell$ とし,C,D を通る直線を $m$ とするとき,以下の問いに答えなさい。(東京都立大2017)
(1) $\ell$ と $m$ が垂直であることを示しなさい。
(2) P を $\ell$ 上の点とし,Q を $m$ 上の点とする。$\overrightarrow{\text{PQ}}$ が $\overrightarrow{\text{AB}}$,$\overrightarrow{\text{CD}}$ の両方に垂直であるとき,P,Q の座標をそれぞれ求めなさい。
(3) K,L を $\ell$ 上の異なる 2 点とし,M,N を $m$ 上の異なる 2 点とする。$\overrightarrow{\text{LK}}$,$\overrightarrow{\text{AB}}$ は同じ向きに平行である,$\overrightarrow{\text{MN}}$,$\overrightarrow{\text{CD}}$ は同じ向き平行であるとする。また,3 つの線分 KL,LM,MN は同じ立方体の 3 つの辺であるとする。このとき,線分 KN の中点の座標を求めなさい。
内角を示す
(1)から始めます。
ベクトルで垂直と言えば,内積 = 0 です。内積を求めましょう。
$\overrightarrow{\text{AB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}$
$=(1,4,0)-(-3,0,2)$
$=(4,4,-2)$
$\overrightarrow{\text{CD}}=\overrightarrow{\text{OD}}-\overrightarrow{\text{OC}}$
$=(2,2,7)-(0,3,5)$
$=(2,-1,2)$
$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{CD}}=4\cdot2+4(-1)+(-2)\cdot2$
$=8-4-4=0$
したがって,$\ell$ と $m$ は垂直である。 (証明終わり)
ベクトル方程式
(2)に進みます。
$\ell$ 上の点 P を表す場合,ベクトル方程式を用いると良いでしょう。
AB 上の点である P をベクトル方程式で表すと
$\overrightarrow{\text{OP}}=\overrightarrow{\text{OA}}+s\overrightarrow{\text{AB}}$ ・・・①
となります。
同様に,CD 上の点 Q は
$\overrightarrow{\text{OQ}}=\overrightarrow{\text{OC}}+t\overrightarrow{\text{CD}}$ ・・・②
です。
$\overrightarrow{\text{PQ}}=\overrightarrow{\text{OQ}}-\overrightarrow{\text{OP}}$
$=\overrightarrow{\text{OC}}+t\overrightarrow{\text{CD}}-\overrightarrow{\text{OA}}-s\overrightarrow{\text{AB}}$
$=(0,3,5)+t(2,-1,2)-(-3,0,2)-s(4,4,-2)$
$=(2t-4s+3,-4s-t+3,2s+2t+3)$ ・・・③
$\text{PQ}\perp\text{AB}$ より
$\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{AB}}=0$
$4(2t-4s+3)+4(-4s-t+3)-2(2s+2t+3)=0$
$-36s+18=0$
$s=\cfrac{1}{2}$ ・・・④
④を①に代入して
$\overrightarrow{\text{OP}}=(-3,0,2)+\cfrac{1}{2}(4,4,-2)$
$=(-1,2,1)$
④を③に代入して
$\overrightarrow{\text{PQ}}=(2t-2+3,-2-t+3,1+2t+3)$
$=(2t+1,1-t,2t+4)$
また,$\text{PQ}\perp\text{CD}$ より
$\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{CD}}=0$
$(2t+1)\cdot2+(1-t)(-1)+(2t+4)\cdot2=0$
$4t+2-1+t+4t+8=0$
$9t+9=0$
$t=-1$
②に代入して
$\overrightarrow{\text{OQ}}=(0,3,5)-(2,-1,2)$
$=(-2,4,3)$
したがって
P$(-1,2,1)$,Q$(-2,4,3)$
(答え)
ベクトルで作る立方体
(3)に進みます。
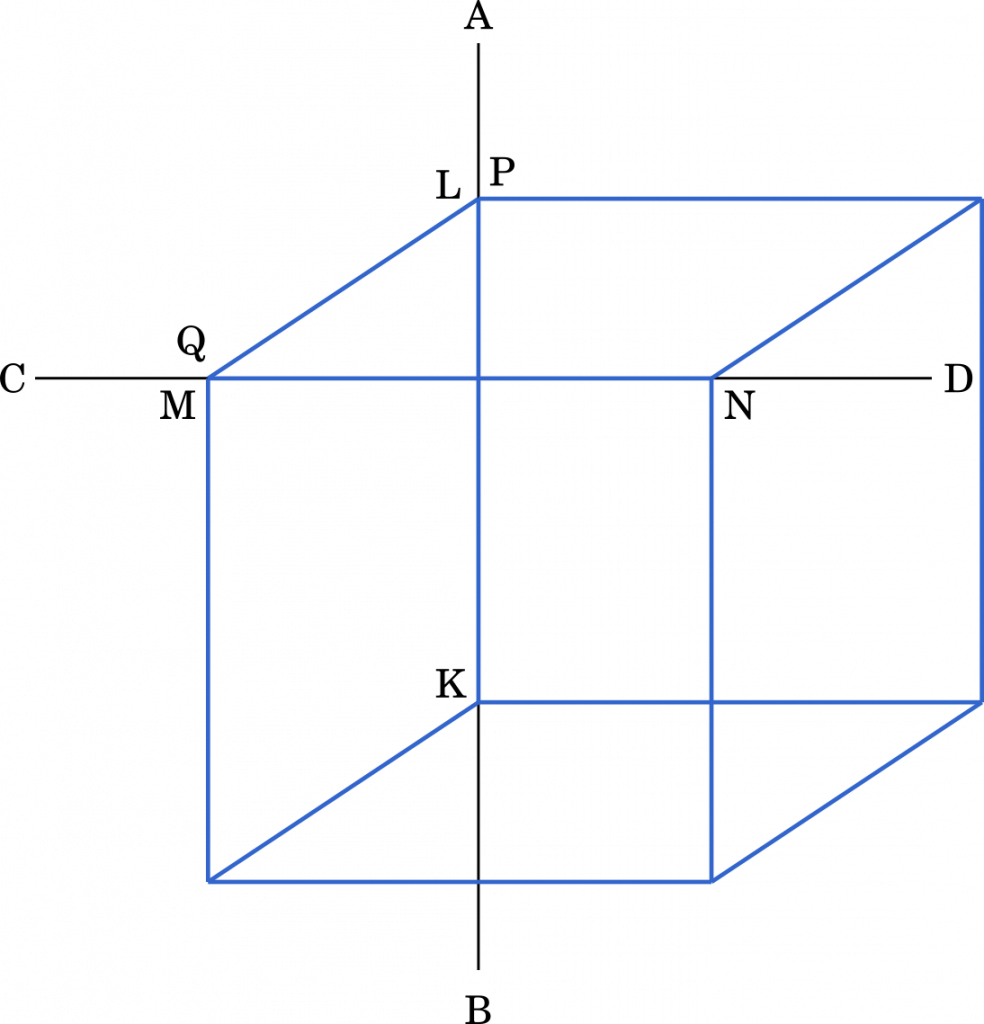
図を描くと上のようになります。$\overrightarrow{\text{LK}}$ の向きを間違えないように注意しましょう。
(2)をもとに考えると,$\ell$ にも $m$ にも垂直な直線は 1 本しか引けません。これが LM になります。
つまり,点 L と(2)で求めた点 P は同じものです。同様に点 M と点 Q も同じものです。

L$(-1,2,1)$
M$(-2,4,3)$
ここから,点 K と点 N の座標を求めれば中点が求められそうです。
立方体なので,辺の長さがすべて同じであることを利用しましょう。まず,座標が分かっている点 L と点 M から長さを求めます。
$\overrightarrow{\text{LM}}=\overrightarrow{\text{OM}}-\overrightarrow{\text{OL}}$
$=(-2,4,3)-(-1,2,1)$
$=(-1,2,2)$
三平方の定理より
$|\overrightarrow{\text{LM}}|=\sqrt{(-1)^2+2^2+2^2}=3$
よって,立方体の辺の長さは 3 です。



長さが 3 のベクトルを考える前に,$\ell$ に平行で長さが 1 のベクトルを考えます。
これを単位ベクトルと言いました。

$\overrightarrow{\text{OK}}=\overrightarrow{\text{OL}}+\overrightarrow{\text{LK}}$ として
$\overrightarrow{\text{OK}}=\overrightarrow{\text{OL}}+3\cdot\cfrac{\overrightarrow{\text{AB}}}{|\overrightarrow{\text{AB}}|}$
この式は,点 L からスタートし,AB に平行で長さが 1 のベクトルを 3 倍して,長さが 3 になる点を求めるということです。
ここで
$|\overrightarrow{\text{AB}}|=\sqrt{4^2+4^2+(-2)^2}=6$
よって
$\overrightarrow{\text{OK}}=\overrightarrow{\text{OL}}+3\cdot\cfrac{\overrightarrow{\text{AB}}}{6}$
$=(-1,2,1)+\cfrac{1}{2}(4,4,-2)$
$=(1,4,0)$
同じ方法で,点 N の座標を求めます。
$\overrightarrow{\text{ON}}=\overrightarrow{\text{OM}}+\overrightarrow{\text{MN}}$
$\overrightarrow{\text{ON}}=\overrightarrow{\text{OM}}+3\cdot\cfrac{\overrightarrow{\text{CD}}}{|\overrightarrow{\text{CD}}|}$
ここで
$|\overrightarrow{\text{CD}}|=\sqrt{2^2+(-1)^2+2^2}=3$
$\overrightarrow{\text{MN}}$ は $m$ に平行で長さが 3 のベクトルなので,たまたまですが,$\overrightarrow{\text{MN}}$ と $\overrightarrow{\text{CD}}$ は同じベクトルであることが分かりました。
よって
$\overrightarrow{\text{ON}}=\overrightarrow{\text{OM}}+\overrightarrow{\text{CD}}$
$=(-2,4,3)+(2,-1,2)$
$=(0,3,5)$
最後に中点を求めましょう。
$\cfrac{1}{2}(\overrightarrow{\text{OK}}+\overrightarrow{\text{ON}})$
$=\cfrac{1}{2}\{(1,4,0)+(0,3,5)\}$
$=\cfrac{1}{2}(1,7,5)$
$=\Big(\cfrac{1}{2},\space\cfrac{7}{2},\space\cfrac{5}{2}\Big)$ (答え)
SNSでシェア