【数Bベクトル】ベクトルで作る三角形の面積を導出する
このページでマスターしたいこと:ベクトルの三角形の公式、三角形の面積の公式、内積
三角形 OPQ において $\overrightarrow{OP}=\vec p,\overrightarrow{OQ}=\vec q$ とおくとき、三角形 OPQ の面積は
$\displaystyle\frac{1}{2}\sqrt{|\vec p|^2|\vec q|^2-(\vec p\cdot\vec q)^2}$
と表されることを証明せよ。(長崎大・改)

この公式、教科書にのってないけど受験生は必須事項。

教科書のってないのに使うって理不尽。

教科書によっては発展事項扱いで出てくる。こういうの言い出すと色々あってキリがないし結局使わずに終わったりするんだけど、その中で言うと割と使う方の公式だから知っておいたほうがいいと思うよ。
公式の形から必要な式を予測する
一度図を描いてみましょう。
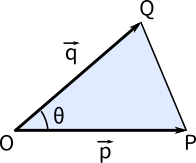
数Ⅰで習った三角形の面積を求める公式 $\displaystyle S=\frac{1}{2}bc\sin A$ より
$\displaystyle \triangle \text{OPQ}=\frac{1}{2}|\vec p||\vec q|\sin \theta\cdots\text{①}$
となります。

ここからどうするんですか?

証明する式の中からヒントを捜して。$\vec p\cdot\vec q$ ってのがあるよね。これ、内積。

ですね。

こういうときは、ともかく内積を作ってみるといいよ。
$\vec p\cdot\vec q=|\vec p||\vec q|\cos \theta\cdots\text{②}$

で、証明する式には $\sin$ とか $\cos$ とかないから、これらを消去する方向で考えるの。
②より
$\displaystyle \cos\theta=\frac{(\vec p\cdot\vec q)}{|\vec p||\vec q|}\\\displaystyle\cos^2\theta=\frac{(\vec p\cdot \vec q)^2}{|\vec p|^2|\vec q|^2}$
また、①は
$\displaystyle \triangle \text{OPQ}=\frac{1}{2}|\vec p||\vec q|\sin \theta\\\displaystyle=\frac{1}{2}|\vec p||\vec q|\sqrt{1-\cos^2\theta}\\\displaystyle=\frac{1}{2}|\vec p||\vec q|\sqrt{1-\frac{(\vec p\cdot\vec q)^2}{|\vec p|^2|\vec q|^2}}$

ここは、三角比の公式から
$\sin^2 x+\cos^2 x=1\\\sin^2 x=1-\cos^2 x\\\sin x=\sqrt{1-\cos^2 x}$
$\sin^2 x+\cos^2 x=1\\\sin^2 x=1-\cos^2 x\\\sin x=\sqrt{1-\cos^2 x}$
あとはルートの外の $|\vec p||\vec q|$ をルートの中に放り込みます。
$\displaystyle=\frac{1}{2}\sqrt{|\vec p|^2|\vec q|^2-(\vec p\cdot\vec q)^2}$
(証明終わり)
SNSでシェア