【数Bベクトル】内積の意味を太陽光発電で理解する　内積量を面積で見える化

太陽光発電に例えてみる

内積の例えとして太陽光発電を考えてみましょう。

ここに光の量 1 がパネルに垂直に入ってきた時 3kw 発電できるパネルがあったとします。

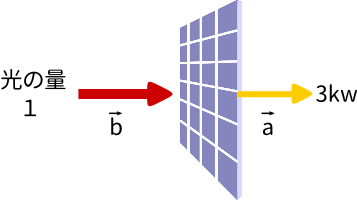
そこに 60°の角度で光が入ってきたとします。このとき、パネルに入ってくる光の量は $\displaystyle1\times\cos 60\text{°}=0.5$ となり、発電量は $0.5\times 3=1.5$ kw となります。

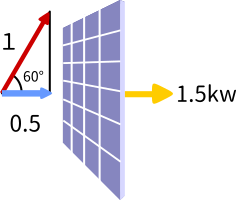
つまり、内積が発電量を表しているということです。光が垂直に入ったときの発電能力を表す黄色のベクトルを $ \vec a$、光を表す赤のベクトルを $\vec b$ とすると、発電量は

$\vec a\cdot\vec b=|\vec a||\vec b|\cos \theta$

として表すことができるのです。

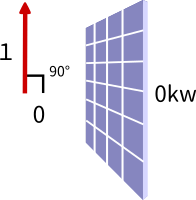
内積を見える化してみる

ベクトルは図形として表すのに内積はスカラー値だから本来、図の上には現れません。そこで少し強引な方法で内積を図形として見える化してみます。

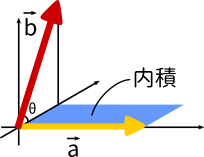
このように片方（ここでは$\vec b$）のベクトルを奥行として軸の向きを変えてやります。こうすると、青で示された四角形の面積が内積を表しています。

逆に言えば、ベクトル同士をかけ算するというのは本来なら目に見えない世界において何らかの量が生まれているということです。物理を習った人なら縦波というのを習ったと思いますが、縦波もまた波の形で目に見えるわけではありません。しかしその変位量の軸を９０°回転させることによって波として見ることができます。上の説明も同じような考え方に基づいて行っています。

内積が役に立つ意味

例えば、$|\vec a +\vec b|^2$ を考えてみましょう。

これは図形として考えるとこのようになります。

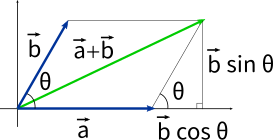
三平方の定理を考えると

$|\vec a +\vec b|^2=(|\vec a|+|\vec b|\cos \theta)^2+|\vec b|^2\sin^2 \theta\\=|\vec a|^2+2|\vec a|\cdot|\vec b|\cos \theta+|\vec b|^2\cos^2\theta+|\vec b|^2\sin^2\theta\\=|\vec a|^2+2\vec a\cdot\vec b+|\vec b|^2(\sin^2\theta+\cos^2\theta)\\=|\vec a|^2+2\vec a\cdot\vec b+|\vec b|^2$

このように内積の定義を用いることで $\cos$ を消すことができます。こうすることで、私たちはベクトルの計算をするときに、いちいち図形上の位置関係を考えることなくベクトルの計算を行うことができるようになるわけです。

結局、実際の計算上では内積が何を意味するのかはあまり意識しません。とは言え本来はベクトルとスカラーの計算はまったく別物なので、今まで習ってきた数学と同じような感覚で計算をしていいものかどうか判断できません。しかし、いったん内積の概念を定義しておけば上のような計算をしてもよい、と言うことができるようになるのです。内積とは計算式を成立させるための影の役割を果たすもの、と理解しておけばよいでしょう。