ベクトル方程式と媒介変数表示の仕組み やってることは一次関数と同じ

ベクトル方程式って習ったけどイマイチ意味が分からないです。

一次関数の考え方をベクトルにしたものだから、そっちから攻めてみると理解できるよ。
ベクトル方程式と一次関数を同じものとしてみなす
ベクトル方程式 $\vec{p}=\vec{a}+t\vec{d}$
例として、$y=3x+5$ という一次関数を考えてみましょう。これをベクトル方程式で表すと、$\vec{p}=(0,5)+t(1,3)$ となります。

なんで?

このグラフ見て。
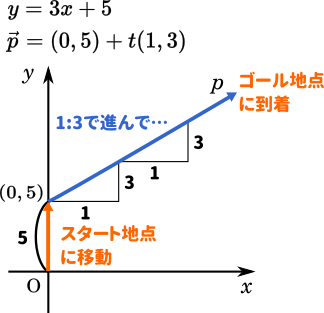

$y=3x+5$ ってのは原点からいったん上に $5$ 移動して、そこから横に $1$、縦に $3$ の比率で $x$ の分だけ移動していく感じだよね。

ゴール地点のところの $y$ 座標が答えですね。

同様に、$\vec{p}=(0,5)+t(1,3)$ は、原点からいったん$(0,5)$ に移動して、そこから横に $1$、縦に $3$ の比率で $t$ の分だけ移動することになる。やってることほぼ一緒だよね。

ベクトル方程式の $(0,5)$ と一次関数の切片って同じことなんですね。

そうそう。さらに $(1,3)$ のところが一次関数でいうところの傾きってこと。そうすると、$t$ のところが一次関数の $x$ になるよね。

じゃあ、一次関数とベクトルって同じことなんですね。

入口の理解としてはそれでオッケー。同じものをベクトルのルールで書いたらベクトル方程式の形になるって思えばいい。
ベクトル方程式と一次関数の違うところ
最初のイメージをつかんだところで、そのイメージを広げていきます。次のベクトル方程式を考えてみましょう。
$$\vec{p}=(2,3)+t(-3,2)$$

んー、切片が $(2,3)$ ってこと?

ベクトル方程式だから本当は切片とは言わないけど、そのイメージでオッケーよ。

で、傾きが $\displaystyle -\frac{2}{3}$ ですか?

そうそう。そういうこと。グラフで書いたらこうなるね。
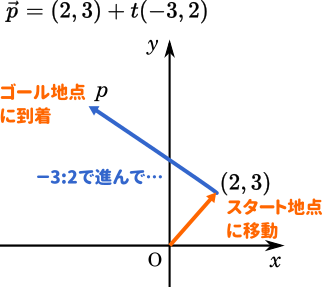

さっきと違うのは、スタート地点まで行くのに斜め方向に移動しているところ。

何か難しくなった。これ意味あるんですか?

一次関数のときはスタート地点、つまり切片は $y$ 軸限定だったじゃない?でもベクトルならどこでもオッケーになる。自由度が高いってのがベクトルのいいところ。
一次関数の式になおす
ここで、式を一次関数として表してみましょう。
まず、$\vec{p}=(2,3)+t(-3,2)$ から $x$ 成分と $y$ 成分をそれぞれ取り出してみましょう。
$x=2-3t,\space y=3+2t$

このとき、式に $t$ を使って表すのを媒介変数表示という。

媒介変数ってどういうことですか?

普通は関数って $y$ イコールなんとか $x$ みたいな形になっていて、$x$ の値が決まれば $y$ の値が決まるよね。$x\rightarrow y$ の流れ。そこに $t$ を挟んで、$x\rightarrow t\rightarrow y$ で $y$ を求める感じ。

なんでそんなやっかいなことするんですか?

$x\rightarrow y$ の流れをいきなり作るのが難しいときに、間に $t$ を入れると式が作りやすくなる場合があるの。今回の場合もだけど、$\vec{p}=(2,3)+t(-3,2)$ からいきなり $x$ と $y$ の関係式作れって言われてもパッとひらめくことはないよね。そういうとき、媒介変数が役に立つ。
$x=2-3t,\space y=3+2t$ より
$3t=2-x$
$\displaystyle t=\frac{2-x}{3}$
$y=3+2t$ に代入して
$\displaystyle y=3+\frac{4-2x}{3}$
$3y=9+4-2x$
$2x+3y-13=0$(答え)

こんな感じで、問題として出されたときは基本的に媒介変数は消去していくことになる。やり方マスターしてね。
SNSでシェア