【数III積分】媒介変数の描く図形の面積・置換積分で攻略！(北海道大2021理系第5問)

座標平面上で，媒介変数 $\theta$ を用いて

$x=(1+\cos\theta)\cos\theta$，$y=\sin\theta$ $(0\leqq\theta<\pi)$

と表される曲線 $C$ がある。$C$ 上の点で $x$ 座標の値が最小になる点を A とし，A の $x$ 座標の値を $a$ とおく。B を点 $(a,0)$，O を原点 $(0,0)$ とする。（北海道大2021）

(1) $a$ を求めよ。

(2) 線分 AB と線分 OB と $C$ で囲まれた部分の面積を求めよ。

x の最小値を求める

(1)から始めます。

問題文から考えると，ようするに $x$ の最小値を求めよ，ということです。

まずは微分してみましょう。かけ算の微分の公式を用います。

$x=(1+\cos\theta)\cos\theta$
$\cfrac{dx}{d\theta}=(1+\cos\theta)’\cos\theta+(1+\cos\theta)(\cos\theta)’$
$=(-\sin\theta)\cos\theta+(1+\cos\theta)(-\sin\theta)$
$=-\sin\theta\cos\theta-\sin\theta-\sin\theta\cos\theta$
$=-2\sin\theta\cos\theta-\sin\theta$
$=-\sin\theta(1+2\cos\theta)$

$-\sin\theta(1+2\cos\theta)=0$ とすると

$\sin\theta=0$ のとき

$\theta=0,\pi$

$1+2\cos\theta=0$ のとき

$\cos\theta=-\cfrac{1}{2}$
$\theta=\cfrac{2}{3}\pi$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline\theta&0&\cdots&\frac{2}{3}\pi&\cdots&\pi\\\hline \frac{dx}{d\theta}&0&-&0&+&0\\\hline x&2&\searrow&-\frac{1}{4}&\nearrow&0\\\hline\end{array}$

$\theta=0$ のとき

$x=(1+\cos0)\cos0$
$=(1+1)\cdot1=2$

$\theta=\cfrac{2}{3}\pi$ のとき

$x=\Big(1+\cos\cfrac{2}{3}\pi\Big)\cos\cfrac{2}{3}\pi$
$=\Big(1-\cfrac{1}{2}\Big)\Big(-\cfrac{1}{2}\Big)$
$=-\cfrac{1}{4}$

$\theta=\pi$ のとき

$x=(1-1)(-1)=0$

したがって，$a=-\cfrac{1}{4}$ （答え）

媒介変数表示された関数から面積を求める

(2)に進みます。

面積を求める前に，グラフのおおまかな形を調べましょう。

$y=\sin\theta$ から，$y$ の値は $\theta=0,\pi$ で $y=0$ になり，$\theta=\cfrac{\pi}{2}$ のとき，$y=1$ になります。

これを表にまとめてみると

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|c|}\hline\theta&0&\cdots&\frac{\pi}{2}&\cdots&\frac{2}{3}\pi&\cdots&\pi\\\hline x&2&\cdots&0&\cdots&-\frac{1}{4}&\cdots&0\\\hline y&0&\cdots&1&\cdots&\frac{\sqrt{3}}{2}&\cdots&0\\\hline\end{array}$

$\theta=\cfrac{\pi}{2}$ のとき

$x=\Big(1+\cos\cfrac{\pi}{2}\Big)\cos\cfrac{\pi}{2}$
$=(1+0)\cdot0=0$

$\theta=\cfrac{2}{3}\pi$ のとき
$y=\sin\cfrac{2}{3}\pi$
$=\cfrac{\sqrt{3}}{2}$

こうして求めた座標をもとにすると，次のような図が出来上がります。

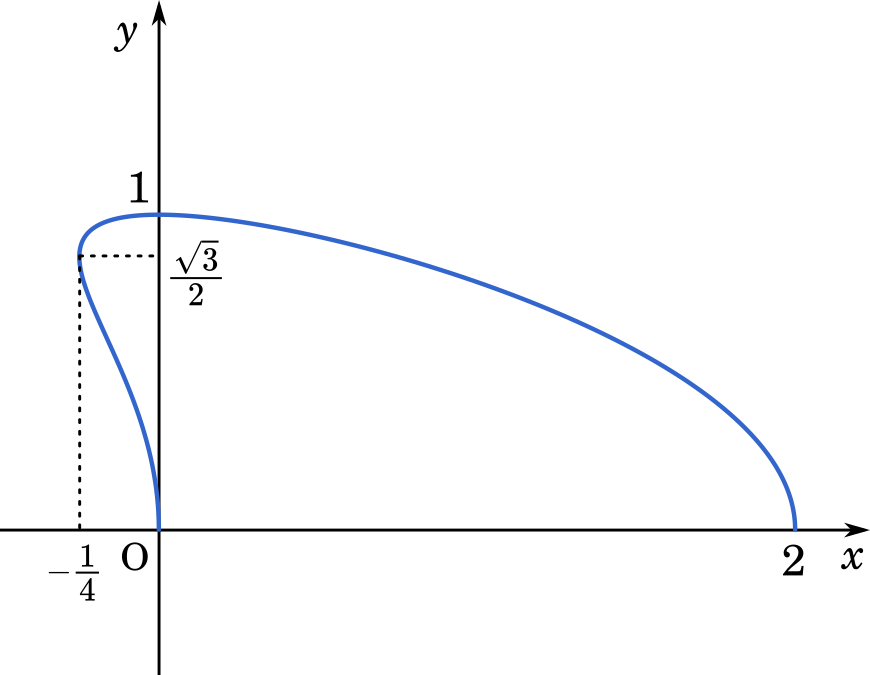
自分でグラフを描くときには，あくまでざっくりしたもので構いません。

ここから，面積を求めてみましょう。積分区間は $\Big[-\cfrac{1}{4},0\Big]$ であり，$y$ の値を積み重ねることで面積を求めることができます。

$S=\displaystyle\int_{-\small\frac{1}{4}}^0 y\space dx$

そこで，置換積分を行います。

$x=(1+\cos\theta)\cos\theta$
$dx=-\sin\theta(1+2\cos\theta)\space d\theta$

よって

$S=\displaystyle\int_{-\small\frac{1}{4}}^0 \sin\theta\space dx$
$\displaystyle S=-\int_{\small\frac{2}{3}\pi}^\pi \sin\theta\sin\theta(1+2\cos\theta)\space d\theta$

$\displaystyle S=-\int_{\small\frac{2}{3}\pi}^\pi \sin^2\theta+2\sin^2\theta\cos\theta\space d\theta$

半角の公式より

$\displaystyle S=-\int_{\small\frac{2}{3}\pi}^\pi \cfrac{1-\cos2\theta}{2}+2\sin^2\theta\cos\theta\space d\theta$

$(\sin^3\theta)’=3\sin^2\theta\cos\theta$ となるので

$=\Big[\cfrac{1}{2}\theta-\cfrac{1}{2}\sin2\theta\cdot\cfrac{1}{2}+\cfrac{2}{3}\sin^3\theta\Big]_{\small\frac{2}{3}\pi}^\pi$

$=-\Big\{\cfrac{\pi}{2}-\cfrac{\pi}{3}+\cfrac{1}{4}\Big(-\cfrac{\sqrt{3}}{2}\Big)-\cfrac{2}{3}\Big(\cfrac{\sqrt{3}}{2}\Big)^3\Big\}$
$=-\cfrac{\pi}{2}+\cfrac{\pi}{3}+\cfrac{\sqrt{3}}{8}-\cfrac{\sqrt{3}}{4}$
$=\cfrac{3\sqrt{3}}{8}-\cfrac{\pi}{6}$ （答え）

媒介変数表示の場合，一般的には媒介変数 $\theta$ を消去して，$y$ と $x$ の式にした上で積分していきます。

今回の場合のように，媒介変数 $\theta$ を消去することが難しい場合は，$x$ を置換積分して $\theta$ の積分に置きかえるとうまくいきます。テクニックとしてマスターしておきましょう。