【数IIベクトル】正四面体でない四面体と外接球の半径(九州大)
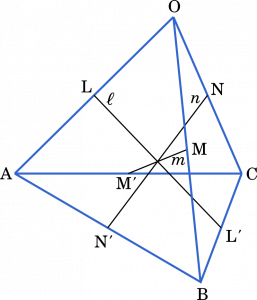
四面体 OABC において,辺 OA の中点と辺 BC の中点を通る直線を $\ell$,辺 OB の中点と辺 CA の中点を通る直線を $m$,辺 OC の中点と辺 AB の中点を通る直線を $n$ とする,$\ell$ ⊥ $m$,$m$ ⊥ $n$,$n$ ⊥ $\ell$ であり,AB = $\sqrt{5}$,BC = $\sqrt{3}$,CA = 2 のとき,以下の問いに答えよ。(九州大2020)
(1) 直線 OB と直線 CA のなす角 $\theta$ $\Big(0$ ≦ $\theta$ ≦ $\cfrac{\pi}{2}\Big)$ を求めよ。
(2) 四面体 OABC の 4 つの頂点をすべて通る球の半径を求めよ。





$\overrightarrow{\text{CA}}=\vec{a}-\vec{c}$ と表せるから,$\vec{a}$,$\vec{b}$,$\vec{c}$ が分かれば答え出せそうね。


条件を式で表す
OA, BC, OB, AB, OC, AC の中点をそれぞれ L, L’, M, M’, N, N’ とおく。
$\overrightarrow{\text{LL’}}=\overrightarrow{\text{OL’}}-\overrightarrow{\text{OL}}$
$=\cfrac{1}{2}\vec{b}+\cfrac{1}{2}\vec{c}-\cfrac{1}{2}\vec{a}$
$=\cfrac{1}{2}(\vec{b}+\vec{c}-\vec{a})$
$\overrightarrow{\text{MM’}}=\cfrac{1}{2}\vec{a}+\cfrac{1}{2}\vec{c}-\cfrac{1}{2}\vec{b}$
$=\cfrac{1}{2}(\vec{a}+\vec{c}-\vec{b})$
$\overrightarrow{\text{NN’}}=\cfrac{1}{2}\vec{a}+\cfrac{1}{2}\vec{b}-\cfrac{1}{2}\vec{c}$
$=\cfrac{1}{2}(\vec{a}+\vec{b}-\vec{c})$
$\ell$ ⊥ $m$ より
$\overrightarrow{\text{LL’}}\cdot\overrightarrow{\text{MM’}}=\cfrac{1}{4}(\vec{b}+\vec{c}-\vec{a})(\vec{a}+\vec{c}-\vec{b})=0$

$\{\vec{c}-(\vec{a}-\vec{b})\}\{\vec{c}+(\vec{a}-\vec{b})\}=0$
$|\vec{c}|^2-|\vec{a}-\vec{b}|^2=0$
$|\vec{c}|^2=|\vec{a}-\vec{b}|^2$
$|\vec{c}|=|\vec{a}-\vec{b}|$

$|\vec{c}|=\sqrt{5}$

$m$ ⊥ $n$ より
$\overrightarrow{\text{MM’}}\cdot\overrightarrow{\text{NN’}}=\cfrac{1}{4}(\vec{a}+\vec{c}-\vec{b})(\vec{a}+\vec{b}-\vec{c})=0$
$\{\vec{a}+(\vec{c}-\vec{b})\}\{\vec{a}-(\vec{c}-\vec{b})\}=0$
$|\vec{a}|=|\vec{c}-\vec{b}|=\sqrt{3}$
$n$ ⊥ $\ell$ より
$\overrightarrow{\text{NN’}}\cdot\overrightarrow{\text{LL’}}=\cfrac{1}{4}(\vec{a}+\vec{b}-\vec{c})(\vec{b}+\vec{c}-\vec{a})=0$
$\{\vec{b}-(\vec{c}-\vec{a})\}\{\vec{b}+(\vec{c}-\vec{a})\}=0$
$|\vec{b}|=|\vec{c}-\vec{a}|=2$
内積を求める


AB = $\sqrt{5}$ より
$|\overrightarrow{\text{AB}}|^2=5$
$|\vec{b}-\vec{a}|^2=5$
$|\vec{b}|^2-2\vec{a}\cdot\vec{b}+|\vec{a}|^2=5$
$4-2\vec{a}\cdot\vec{b}+3=5$
$2\vec{a}\cdot\vec{b}=2$
$\vec{a}\cdot\vec{b}=1$
同様にして
$|\vec{c}-\vec{b}|^2=3$ より
$\vec{b}\cdot\vec{c}=3$
$|\vec{a}-\vec{c}|^2=4$ より
$\vec{a}\cdot\vec{c}=2$

$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{CA}}=\vec{b}\cdot(\vec{a}-\vec{c})$
$=\vec{a}\cdot\vec{b}-\vec{b}\cdot\vec{c}$
$=1-3=-2$
また
$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{CA}}=|\overrightarrow{\text{OB}}||\overrightarrow{\text{CA}}|\cos\theta$
$2\cdot2\cos\theta=-2$
$\cos\theta=-\cfrac{1}{2}$
$\theta=\cfrac{2}{3}\pi$



0 ≦ $\theta$ ≦ $\cfrac{\pi}{2}$ より
$\theta=\cfrac{\pi}{3}$ (答え)





2 直線の位置関係から外接球の中心を求める






$\overrightarrow{\text{CA}}\cdot\overrightarrow{\text{MM’}}=(\vec{a}-\vec{c})\cdot\cfrac{1}{2}(\vec{a}+\vec{c}-\vec{b})$
=$\cfrac{1}{2}(|\vec{a}|^2+\vec{a}\cdot\vec{c}-\vec{a}\cdot\vec{b}-\vec{a}\cdot\vec{c}-|\vec{c}|^2+\vec{b}\cdot\vec{c})$
$=\cfrac{1}{2}(3+2-1-2-5+3)=0$
$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{MM’}}=\vec{b}\cdot\cfrac{1}{2}(\vec{a}+\vec{c}-\vec{b})$
$=\cfrac{1}{2}(\vec{a}\cdot\vec{b}+\vec{b}\cdot\vec{c}-|\vec{b}|^2)$
$=\cfrac{1}{2}(1+3-4)=0$
よって,CA ⊥ MM’,OB ⊥ MM’
$|\text{MM’}|^2=\cfrac{1}{4}(\vec{a}+\vec{c}-\vec{b})^2$
$=\cfrac{1}{4}(|\vec{a}|^2+|\vec{c}|^2+|\vec{b}|^2-2\vec{a}\cdot\vec{b}-2\vec{b}\cdot\vec{c}+2\vec{a}\cdot\vec{c})$
$=\cfrac{1}{4}(3+5+4-2\cdot1-2\cdot3+2\cdot2)$
$=2$
$|\text{MM’}|=\sqrt{2}$
よって PM = $\cfrac{\sqrt{2}}{2}$
また OB = 2 より,OM = 1 だから,三平方の定理より
$\text{OP}^2=1^2+\Big(\cfrac{\sqrt{2}}{2}\Big)^2=\cfrac{3}{2}$
OP = $\cfrac{\sqrt{6}}{2}$ (答え)

SNSでシェア