【スマホで読む・わかりやすい】センター数学IA2019追試【解説・正解・問題】
第1, 2問必答。第3~5問はいずれか2問を選択し, 解答。
第1問 正解と解説
アイ ウ -2 3
エ オ カ キ 2 3 2 6 又は 2 6 2 3
ク 6 ケ 6 コ サ シ 6 2 3
ス 5 セ 2 ソ 4 タ 0 チ 1
ツ テ 4 3 ト 2 ナ ニ 1 3
ヌ0 ネ 3
〔1〕(1)
$f(0)$ ≦ 6 のとき
$f(0)=-\sqrt{3}a$ ≦ 6
$a$ ≧ $-\cfrac{6}{\sqrt{3}}$
$a$ ≧ $-2\sqrt{3}$
・・・アイウ
$f(6)$ ≧ 0 のとき
$f(6)=(1+\sqrt{2})\cdot6-\sqrt{3}a$ ≧ 0
$\sqrt{3}a$ ≦ $6(1+\sqrt{2})$
$a$ ≦ $\cfrac{6(1+\sqrt{2})}{\sqrt{3}}$
$a$ ≦ $2\sqrt{3}(1+\sqrt{2})$
$a$ ≦ $2\sqrt{3}+2\sqrt{6}$
・・・エオカキ
(2)
P と Q の中点を求めると
$\cfrac{-2\sqrt{3}+2\sqrt{3}+2\sqrt{6}}{2}=\sqrt{6}$
・・・ク
(3)
$f(0)$ ≦ 6 かつ $f(6)$ ≧ 0 のとき
$-2\sqrt{3}$ ≦ $a$ ≦ $2\sqrt{3}+2\sqrt{6}$
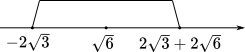
ここで絶対値とは数直線における原点からの距離であることに注意すると,中点の位置を 0 に移動することで絶対値の範囲を求めることができる。
$-2\sqrt{3}-\sqrt{6}$ ≦ $a-\sqrt{6}$ ≦ $2\sqrt{3}+\sqrt{6}$

したがって
$|a-\sqrt{6}|$ ≦ $\sqrt{6}+2\sqrt{3}$
・・・ケコサシ
〔2〕(1)
$p\implies q$ の逆は $q\implies p$ だから
($n$ > 2 かつ $n$ < $c$) $\implies n^2-8n+15=0$
・・・ス
$p\implies q$ の対偶は $\overline{q}\implies\overline{p}$ である。
ド・モルガンの法則より,$\overline{A\cap B}=\overline{A}\cup\overline{B}$ だから
($n$ ≦ 2 または $n$ ≧ $c$) $\implies n^2-8n+15$ ≠ 0
・・・セ
〔2〕(2)
$p$ が $q$ であるための必要条件でないとき,$q\implies p$ は偽である。
$p:n^2-8n+15=0$
$(n-3)(n-5)=0$
$n$ = 3,5
ここで $c$ = 5 のときを考えると,$q$ は「$n$ > 2 かつ $n$ < 5」となる。これに含まれる数は 3 と 4 である。このとき 3 は $p$ に含まれるが 4 は含まれない。$c$ が 5 以上のときも同様だから,$n$ = 4 はつねに命題「$q\implies p$」の反例となる。
・・・ソ
〔2〕(3)
$p$ が $q$ であるための十分条件でないとき,$p\implies q$ は偽であり $p\implies q$ は真,偽どちらでもよい。
条件 $p$ は「$n$ は 3 または 5」だから,$c$ = 4 のとき $n$ < 4 となるので $p\implies q$ は偽となる。
・・・タ
〔2〕(4)
$\overline{B}$ ={$k$|$k$ < $c$}となるので,$q$ と同値になるのは,$n \in A\cap\overline{b}$ のとき。
・・・チ
〔3〕(1)
方程式が異なる二つの実数解を持つとき,判別式 $D$ > 0 だから
$\cfrac{D}{4}=(2a-b)^2-b(b-4a+3)$ > 0
$4a^2-4ab+b^2-b^2+4ab-3b$ > 0
$4a^2-3b$ > 0
$3b$ < $4a^2$
$b$ < $\cfrac{4}{3}a^2$
・・・ツテ
また
$x=\cfrac{b-2a\pm\sqrt{4a^2-3b}}{b}$
・・・ト
〔3〕(2)
$b=a^2$ とおき,判別式 $\cfrac{D}{4}=4a^2-3b$ に代入すると
$\cfrac{D}{4}=4a^2-3a^2=a^2$
$a$ ≠ 0 より $a^2$ は 0 以上の値だから,つねに異なる二つの実数解を持つ。また,解を求めると
$x=\cfrac{a^2-2a\pm\sqrt{a^2}}{a^2}$
$=\cfrac{a^2-2a\pm|a|}{a^2}$
($a^2$はつねに正の値だから,$\sqrt{a^2}$ はつねに正の値をとる。よって $|a|$ としなければならない。)
ここで,分母は $a^2$ だからつねに正の値である。よって,分子について一方が正の値,他方が負の値になる場合を考えるとよい。
$a$ が正の値のとき
$a^2-2a\pm|a|=a^2-2a\pm a$
$a$ が負の値のとき
$a^2-2a\pm|a|=a^2-2a\mp a$
よって,$a$ が正の値でも負の値でも分子は $a^2-2a\pm a$ でよい。
一方が正の解であるとき
$a^2-2a+a$ > 0
$a^2-a$ > 0
$a(a-1)$ > 0
$a$ < 0,$a$ > 1
他方が負の解であるとき
$a^2-2a-a$ < 0
$a^2-3a$ < 0
$a(a-3)$ < 0
0 < $a$ < 3
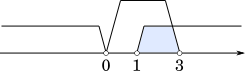
したがって 1 < $a$ < 3
・・・ナニ
また,いずれも正の解であるとき
$a^2-2a+a$ > 0
$a$ < 0,$a$ > 1
また
$a^2-2a^a$ > 0
$a(a-3)$ > 0
$a$ < 0,$a$ > 3
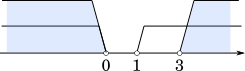
したがって $a$ < 0,$a$ > 3
・・・ヌネ
問題文
〔1〕
〔1〕$a$ を実数とする。$x$ の関数
$f(x)=(1+\sqrt{2})x-\sqrt{3}a$
を考える。
(1) $f(0)$ ≦ 6 となるような $a$ の値の範囲は
$a$ ≧ $\boxed{\text{アイ}}\sqrt{\boxed{\text{ウ}}}$
であり, $f(6)$ ≧ 0 となるような $a$ の値の範囲は
a ≦ $\boxed{\text{エ}}\sqrt{\boxed{\text{オ}}}+\boxed{\text{カ}}\sqrt{\boxed{\text{キ}}}$
である。ただし, $\boxed{\text{エ}}\sqrt{\boxed{\text{オ}}}$,$\boxed{\text{カ}}\sqrt{\boxed{\text{キ}}}$ の解答の順序は問わない。
(2) 数直線において, 実数 $\boxed{\text{アイ}}\sqrt{\boxed{\text{ウ}}}$ を表す点を P とし, 実数 $\boxed{\text{エ}}\sqrt{\boxed{\text{オ}}}+\boxed{\text{カ}}\sqrt{\boxed{\text{キ}}}$ を表す点を Q とするとき, 線分 PQ の中点に対応する実数は $\sqrt{\boxed{\text{ク}}}$ である。
(3) 一般に, 実数 $u$ と, 0 以上の実数 $r$ に対し
$|u|$ ≦ $r$ $\iff$ $-r$ ≦ $u$ ≦ $r$
が成り立つことに注意すると, $f(0)$ ≦ 6 かつ $f(6)$ ≧ 0 となるような $a$ の値の範囲は, 絶対値を含む不等式
$|a-\sqrt{\boxed{\text{ケ}}}|$ ≦ $\sqrt{\boxed{\text{コ}}}+\boxed{\text{サ}}\sqrt{\boxed{\text{シ}}}$
を満たす $a$ の値の範囲に一致する。
〔2〕$c$ を 4 以上の整数とする。整数 $n$ に関する二つの条件 $p$, $q$ を次のように定める。
$p$:$n^2-8n+15=0$
$q$:$n$ > 2 かつ $n$ < $c$
(1) 次の $\boxed{\text{ス}}$,$\boxed{\text{セ}}$ に当てはまるものを, 下の⓪~⑤のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。
命題「$p \implies q$」の逆は「$\boxed{\text{ス}}$」である。また, 命題「$p\implies q$」の対偶は「$\boxed{\text{セ}}$」である。
⓪ $n^2-8n+15$ ≠ 0 $\implies$ ($n$ ≦ 2 または $n$ ≧ $c$ )
① $n^2-8n+15$ ≠ 0 $\implies$ ( $n$ ≦ 2 かつ $n$ ≧ $c$ )
② ( $n$ ≦ 2 または $n$ ≧ $c$ ) $\implies$ $n^2-8n+15$ ≠ 0
③ ( $n$ > 2 かつ $n$ < $c$ ) $\implies$ $n^2-8n+15$ ≠ 0
④ ( $n$ ≦ 2 または $n$ ≧ $c$ ) $\implies$ $n^2-8n+15=0$
⑤ ( $n$ > 2 かつ $n$ < $c$ ) $\implies$ $n^2-8n+15=0$
(2) 整数 $c$ が 5 以上のとき, $p$ は $q$ であるための必要条件ではない。なぜならば, 整数 $c$ が 5 以上のとき, 整数 $n=\boxed{\text{ソ}}$ はつねに命題「$q$ $\implies$ $q$」の反例となるからである。
(3) 次の $\boxed{\text{タ}}$ に当てはまるものを, 下の⓪~③のうちから一つ選べ。
整数 $c$ が $\boxed{\text{タ}}$ を満たすとき, $p$ は $q$ であるための十分条件ではない。
⓪ $c$=4 ① $c$ > 5 ② $c$=6 ③ $c$ > 7
(4) 整数全体の集合を全体集合とし, その部分集合 $A$, $B$ を
$A$={$k$|$k$ > 2},$B$={$k$|$k$ ≧ $c$}
と定める。集合 $A$, $B$ の補集合をそれぞれ $\overline{A}$, $\overline{B}$ で表す。
次の $\boxed{\text{チ}}$ に当てはまるものを, 下の⓪~⑤のうちから一つ選べ。
整数 $n$ に関する次の条件のうち, $q$ と同値である条件は $\boxed{\text{チ}}$ である。
⓪ $n$ ∈ $A$ ∩ $B$ ① $n$ ∈ $A$ ∩ $\overline{B}$
② $n$ ∈ $\overline{A}$ ∩ $B$ ③ $n$ ∈ $A$ ∪ $B$
④ $n$ ∈ $A$ ∪ $\overline{B}$ ③ $n$ ∈ $\overline{A}$ ∪ $B$
〔3〕$a$ と $b$ はいずれも 0 でない実数とする。$x$ の方程式
$bx^2+2(2a-b)x+b-4a+3=0\cdots\cdots$①
を考える。
(1) 方程式①が異なる二つの実数解をもつのは
$b$ < $\cfrac{\boxed{\text{ツ}}}{\boxed{\text{テ}}}\enspace a^2$
のときである。このとき, 二つの実数解は
$x=\cfrac{b-\boxed{\text{ト}}a\pm\sqrt{\boxed{\text{ツ}}a^2-\boxed{\text{テ}}b}}{b}$
である。
(2) $b=a^2$ とする。方程式①が異なる二つの実数解をもち, それらの一方が正の解で他方が負の解であるような $a$ の値の範囲は
$\boxed{\text{ナ}}$ < $a$ < $\boxed{\text{ニ}}$
である。また, 方程式①が異なる二つの実数解をもち, それらがいずれも正の解であるような $a$ の値の範囲は
$a$ < $\boxed{\text{ヌ}}$, $a$ > $\boxed{\text{ネ}}$
である。
SNSでシェア