【スマホで読む・わかりやすい】センター数学IIB2016本試【解説・正解・問題】

第1問　解答・解説

ア イ 4 2　ウエ オ －2 3　カ 2　キ 3

ク 1　ケ 1　コ サ 6 7　シ 3

ス,セ 3, 8　ソタ －2　チ 4　ツ 4

テ ト 1 4　ナ 3　ニ 1　ヌ ネ 4 5

ノハ ヒ －3 5　フ ヘ 5 5

〔1〕

(1)

$8^{\small{\frac{5}{6}}}=2^{\small{3\cdot\frac{5}{6}}}=2^{\small{\frac{5}{2}}}$

$=(\sqrt{2})^5=4\sqrt{2}$

・・・アイ

(2)

$\log_{27}\cfrac{1}{9}=\log_{27}1-\log_{27}9$

$=-\log_{27}9$

$=-\cfrac{\log_39}{\log_327}=\cfrac{-2}{3}$

・・・ウエオ

(2)

(i) $y=2^x$ と $y=\Big(\cfrac{1}{2}\Big)^2$

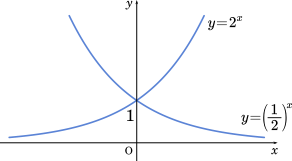
グラフは $y$ 軸に関して対称である。

・・・カ

(ii) $y=2^x$ と $y=\log_2 x$

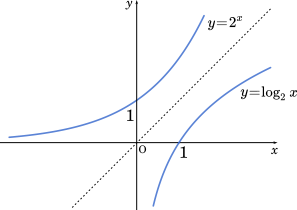
グラフは直線 $y=x$ に関して対称である。

・・・キ

(iii) $y=\log_2 x$ と $y=\log_{\small{\frac{1}{2}}}x$

$\log_{\small{\frac{1}{2}}}x=\cfrac{\log_2x}{\log_2\cfrac{1}{2}}=-\log_2 x$

したがって，グラフは $x$ 軸に関して対称である。

・・・ク

(iv) $y=\log_2 x$ と $y=\log_2\cfrac{1}{x}$

$\log_2\cfrac{1}{x}=\log_21-\log_2x=-\log_2x$

したがって，グラフは $x$ 軸に関して対称である。

・・・ケ

(3)

$y=\Big(\log_2\cfrac{x}{4}\Big)^2-4\log_4x+3$

$=(\log_2x-\log_24)^2-4\cfrac{\log_2x}{\log_24}+3$

$=(\log_2x-2)^2-2\log_2x+3$

$t=\log_2x$ とおくと

$=(t-2)^2-2t+3$

$=t^2-4t+4-2t+3$

$=t^2-6t+7$

・・・コサ

$x$ が $x\gt0$ の範囲を動くとき，$t$ のとり得る値の範囲は実数全体である。

・・・シ

最小値を求めるために式を平方完成すると

$=(t-3)^2-9+7$

$=(t-3)^2-2$

したがって，$t=3$ のとき，すなわち

$3=\log_2x$

$x=2^3=8$

のとき，最小値 $-2$ をとる。

・・・スセソタ

〔2〕

(1)

①の両辺に $\sin^2x\cos^2x$ をかけると

$\sin^2x\cos^2x\Big\{\cos^2x-\sin^2x+k\Big(\cfrac{\sin^2x-\cos^2x}{\sin^2x\cos^2x}\Big)\Big\}=0$

$\cfrac{1}{4}(4\sin^2 x\cos^2 x)\Big\{\cos^2x-\sin^2x+4k\Big(\cfrac{\sin^2x-\cos^2x}{4\sin^2x\cos^2x}\Big)\Big\}=0$

2 倍角の公式 $\sin2x=2\sin x\cos x$，$\cos2x=\cos^2x-\sin^2x$ より

$\cfrac{1}{4}\sin^2 2x\Big(\cos2x-\cfrac{4k\cos2x}{\sin^2 2x}\Big)=0$

$\cfrac{\sin^2 2x\cos 2x}{4}-k\cos2x=0$

$\Big(\cfrac{\sin^2 2x}{4}-k\Big)\cos 2x=0\cdots\cdots$②

・・・チ

②は，$\cfrac{\sin^2 2x}{4}-k=0$ または $\cos2x=0$ のときに恒等式が成り立つ。

よって，$\cos 2x=0$ とおき, $x$ を求めると

$2x=\cfrac{\pi}{2}$

$x=\cfrac{\pi}{4}$

したがって，$x=\cfrac{\pi}{4}$ のときは常に①が成り立つ。

・・・ツ

また，$\cfrac{\sin^2 2x}{4}-k=0$ とおくと

$k=\cfrac{\sin^2 2x}{4}$

ここで，$k$ の値のとり得る範囲を求めると

$0\lt\sin^2 2x\leqq1$ より

$0\lt\cfrac{\sin^22x}{4}\leqq\cfrac{1}{4}$

$0\lt k\leqq\cfrac{1}{4}$

$k\gt\cfrac{1}{4}$ のとき，$\cfrac{\sin^2 2x}{4}-k=0$ を満たす $x$ は存在しないので，①を満たす $x$ は $\cos2x=0$，つまり $x=\cfrac{\pi}{4}$ のみである。

・・・テト

一方，$0\lt k\lt\cfrac{1}{4}$ のとき

$0\lt x\lt\cfrac{\pi}{2}$

$0\lt 2x\lt \pi$

となるので，$\cfrac{\sin^2 2x}{4}-k=0$ を満たす $x$ は $0\lt x\lt \cfrac{\pi}{2}$ の範囲と，$\cfrac{\pi}{2}\leqq x\lt \pi$ の範囲にそれぞれ 1 つずつ存在する。これに $\cos 2x=0$ を満たす $x$ を加えて，①を満たす $x$ の個数は $3$ 個である。

また，解が重解にならず，つねに 3 個になることを確認する。$x=\cfrac{\pi}{4}$ のとき，$k=\cfrac{\sin^2 2x}{4}=\cfrac{1}{4}$ となるが，$k$ の範囲は $0\lt k\lt\cfrac{1}{4}$ だから，解は存在しない。よって解の個数はつねに 3 個である。

・・・ナ

このことより，$k=\cfrac{1}{4}$ のときは，$\cos2x=0$ つまり $x=\cfrac{\pi}{4}$ のみが解となる。したがって，解は 1 個。

・・・ニ

(2)

$k=\cfrac{4}{25}$ とすると，②は

$\Big(\cfrac{\sin^2 2x}{4}-\cfrac{4}{25}\Big)\cos 2x=0$

$\cfrac{\sin^22x}{4}-\cfrac{4}{25}=0$ のとき

$\cfrac{\sin^22x}{4}=\cfrac{4}{25}$

$\sin^22x=\cfrac{16}{25}$

$\sin2x=\pm\cfrac{4}{5}$

・・・ヌネ

$\cfrac{\pi}{4}\lt x\lt\cfrac{\pi}{2}$ を変形すると $\cfrac{\pi}{2}\lt 2x\lt \pi$ となり，$\sin$ は正の値をとるので

$\sin2x=\cfrac{4}{5}$

公式 $\sin^2x+\cos^2x=1$ より

$\Big(\cfrac{4}{5}\Big)^2+\cos^22x=1$

$\cos^22x=\cfrac{9}{25}$

$\cos 2x=\pm\cfrac{3}{5}$

$\cfrac{\pi}{2}\lt 2x\lt \pi$ より，$\cos$ は負の値をとるので

$\cos2x=\cfrac{-3}{5}$

・・・ノハヒ

半角の公式 $\cos^2 x=\cfrac{1+\cos 2x}{2}$ を用いて

$\cos^2 x=\cfrac{1-\cfrac{3}{5}}{2}=\cfrac{\cfrac{2}{5}}{\space2\space}=\cfrac{1}{5}$

$\cos x=\pm\cfrac{\sqrt{5}}{5}$

$\cfrac{\pi}{4}\lt x\lt\cfrac{\pi}{2}$ より，$\cos$ は正の値をとるので

$\cos x=\cfrac{\sqrt{5}}{5}$

・・・フヘ

第1問　問題文

〔1〕

(1) $8^{\small{\frac{5}{6}}}=\boxed{\text{ア}}\sqrt{\boxed{\text{イ}}},\enspace\log_{27}\cfrac{1}{9}=\cfrac{\boxed{\text{ウエ}}}{\boxed{\text{オ}}}$ である。

(2) $y=2^x$ のグラフと $y=\Big(\cfrac{1}{2}\Big)^2$ のグラフは $\boxed{\text{カ}}$ である。

$y=2^x$ のグラフと $y=\log_2x$ のグラフは $\boxed{\text{キ}}$ である。

$y=\log_2 x$ のグラフと $y=\log_{\frac{1}{2}}x$ のグラフは $\boxed{\text{ク}}$ である。

$y=\log_2x$ のグラフと $y=\log_2\cfrac{1}{x}$ のグラフは $\boxed{\text{ケ}}$ である。

$\boxed{\text{カ}}$~$\boxed{\text{ケ}}$ に当てはまるものを, 次の⓪~③のうちから一つずつ選べ。ただし, 同じものを繰り返し選んでもよい。

⓪ 同一のもの　① $x$ 軸に関して対称

② $y$ 軸に関して対称　③ 直線 $y=x$ に関して対称

(3) $x\gt0$ の範囲における関数 $y=\Big(\log_2\cfrac{x}{4}\Big)^2-4\log_4x+3$ の最小値を求めよう。

$t=\log_2x$ とおく。このとき, $y=t^2-\boxed{\text{コ}}t+\boxed{\text{サ}}$ である。また, $x$ が $x\gt0$ の範囲を動くとき, $t$ のとり得る値の範囲は, $\boxed{\text{シ}}$ である。$\boxed{\text{シ}}$ に当てはまるものを, 次の⓪~③のうちから一つ選べ。

⓪ $t\gt0$　① $t\gt1$

② $t\gt0$ かつ $t\not= 1$　③ 実数全体

したがって, $y$ は $t=\boxed{\text{ス}}$ のとき, すなわち $x=\boxed{\text{セ}}$ のとき, 最小値 $\boxed{\text{ソタ}}$ をとる。

〔2〕 $k$ を正の定数として

$\cos^2 x-\sin^2 x+k\Big(\cfrac{1}{\cos^2x}-\cfrac{1}{\sin^2 x}\Big)=0\cdots\cdots$①

を満たす $x$ について考える。

(1) $0\lt x\lt\cfrac{\pi}{2}$ の範囲で①を満たす $x$ の個数について考えよう。

①の両辺に $\sin^2 x\cos^2 x$ をかけ, 2 倍角の公式を用いて変形すると

$\Big(\cfrac{\sin^2 2x}{\boxed{\text{チ}}}-k\Big)\cos 2x=0\cdots\cdots$②

を得る。したがって, $k$ の値に関係なく, $x=\cfrac{\pi}{\boxed{\text{ツ}}}$ のときはつねに①が成り立つ。また, $0\lt x\lt\cfrac{\pi}{2}$ の範囲で $0\lt\sin^2 2x\leqq1$ であるから, $k\gt\cfrac{\boxed{\text{テ}}}{\boxed{\text{ト}}}$ のとき, ①を満たす $x$ は $\cfrac{\pi}{\boxed{\text{ツ}}}$ のみである。一方, $0\lt k\lt\cfrac{\boxed{\text{テ}}}{\boxed{\text{ト}}}$ のとき, ①を満たす $x$ の個数は $\boxed{\text{ナ}}$ 個であり,

$k=\cfrac{\boxed{\text{テ}}}{\boxed{\text{ト}}}$ のときは, $\boxed{\text{ニ}}$ 個である。

(2) $k=\cfrac{4}{25}$ とし, $\cfrac{\pi}{4}\lt \pi\lt\cfrac{\pi}{2}$ の範囲で①を満たす $x$ について考えよう。

②により $\sin 2x=\cfrac{\boxed{\text{ヌ}}}{\boxed{\text{ネ}}}$ であるから

$\cos 2x=\cfrac{\boxed{\text{ノハ}}}{\boxed{\text{ヒ}}}$

である。したがって

$\cos x=\cfrac{\sqrt{\boxed{\text{フ}}}}{\boxed{\text{ヘ}}}$

である。