【スマホで読む・わかりやすい】センター数学IIB2015追試【解説・正解・問題】

第1問　解答・解説

ア 0　イ,ウエ 2,12　オ 2　カ,キ 4,2

ク,ケ 3,2　コ 9　サ 6　シ 4

スセ 25　ソ 6　タチ 10　ツ,テ 3,4

ト,ナ 8,6　ニ,ヌ 5,2　ネ 3

ノハ,ヒ 25,6　フ,ヘ,ホ 4,3,3

〔1〕

真数条件より，$y\gt0$

・・・ア

$z=2^x$ とおくと

$2^{x-2}+\cfrac{1}{2}y=3$

$\cfrac{2^x}{2^2}+\cfrac{1}{2}y=3$

$\cfrac{z+2y}{4}=3$

$z+2y=12$

また，$z=2^x$ は $x=\log_2 z$ と書き換えることができるので

$\begin{cases}z+2y-12\cdots\cdots\text{①}\\\log_2 z-\log_{\sqrt{2}}y=2\cdots\cdots\text{②}\end{cases}$

・・・イウエ

次に，$w=\log_{\sqrt{2}}y$ とおくと，$y=(\sqrt{2})^w$ となるので，2 を底として両辺の対数をとると

$y=(\sqrt{2})^w$

$\log_2 y=\log_2(\sqrt{2})^w$

$\log_2 y=w\log_2 \sqrt{2}$

$\log_2 y=w\log_2 2^{\small\frac{1}{2}}$

$\log_2 y=\cfrac{1}{2}w\log_2 2$

$\log_2 y=\cfrac{1}{2}w$

$w=2\log_2 y$

・・・オ

これを用いて，②は

$\log_2 z-\log_{\sqrt{2}} y=2$

$w=\log_{\sqrt{2}}y=2\log_2 y$ だから

$\log_2 z-2\log_2 y=2$

$\log_2 z-\log_2 y^2=2$

$\log_2 \cfrac{z}{y^4}=2$

$\cfrac{z}{y^2}=2^2$

$z=4y^2\cdots\cdots$③

・・・カキ

①と③を連立すると

$4y^2+2y=12$

$2y^2+y-6=0$

$(2y-3)(y+2)=0$

$y=\cfrac{3}{2},-2$

・・・クケコ

$y\gt0$ より $y=\cfrac{3}{2}$

①に代入して

$z+2\cdot\cfrac{3}{2}=12$

$z=9$

したがって，$9=2^x$ となるので

$x=\log_2 9$

よって，$x+y=\log_2 9+\cfrac{3}{2}$ となり，これ以下の整数のうちで最大のものを求める。

$\cfrac{n}{2}\leqq\log_2 9\lt\cfrac{n+1}{2}$

とおくと，$x=\log_2 9$ より $2^x=9$ となるので，$x\gt3$ が成り立つ。よって

$3\lt\log_2 9$

ここで，$\cfrac{n}{2}=3$ とすると，$n=6$

・・・サ

これを代入して，$\cfrac{n+1}{2}=\cfrac{7}{2}$

よって，不等式の右側は

$\log_2 9\lt\cfrac{7}{2}$

$\log_2 9+\cfrac{3}{2}\lt\cfrac{7}{2}+\cfrac{3}{2}$

$\log_2 9+\cfrac{3}{2}\lt5$

となり，$x+y$ 以下の整数のうちで最大のものは $4$ である。

・・・シ

〔2〕

(1)

円 $C$ の方程式は

$x^2+y^2=25$

・・・スセ

(2)

△OAP と △OAQ は3辺の長さがそれぞれ等しいので，合同である。したがって，∠OAP = ∠OAQ となるので，∠OAP = $\cfrac{\pi}{6}$

・・・ソ

このことより，△OAP はそれぞれの辺の比が $1:2:\sqrt{3}$ の直角三角形であることが分かる。OP = $5$ だから，OA = $10$

・・・タチ

また，OA ⊥ PQ より，直線 OA の傾きを $m$ とおくと

$-\cfrac{4}{3}m=-1$

$m=\cfrac{3}{4}$

・・・ツテ

したがって，直線 OA の方程式は

$y=\cfrac{3}{4}x$

点 A の座標を $\bigg(x,\cfrac{3}{4}x\bigg)$ とすると，三平方の定理より

$\text{OA}^2=x^2+\bigg(\cfrac{3}{4}x\bigg)^2$

$10^2=x^2+\cfrac{9}{16}x^2$

$\cfrac{25}{16}x^2=100$

$x^2=64$

$x=8$

よって

$y=\cfrac{3}{4}\cdot8=6$

したがって，A の座標は $(8,6)$

・・・トナ

(3)

∠POR = $\cfrac{\pi}{3}$ だから，△OPR はそれぞれの辺の比が $1:2:\sqrt{3}$ の直角三角形である。よって

OP : OR = $2:1$

$5$ : OR = $2:1$

$2\text{OR}=5$

OR = $\cfrac{5}{2}$

・・・ニヌ

また

OR : RA = $\cfrac{5}{2}:\bigg(10-\cfrac{5}{2}\bigg)$

OR : RA = $1:3$

・・・ネ

これを用いて R の座標を求めると，A の座標が $(8,6)$ だから

$\bigg(\cfrac{8}{4},\cfrac{6}{4}\bigg)$

$=\bigg(2,\cfrac{3}{2}\bigg)$

直線 PQ の方程式は，傾きが $-\cfrac{4}{3}$ であることに注意して

$y-\cfrac{3}{2}=-\cfrac{4}{3}(x-2)$

$y=-\cfrac{4}{3}x+\cfrac{8}{3}+\cfrac{3}{2}$

$y=-\cfrac{4}{3}x+\cfrac{25}{6}$

・・・ノハヒ

円 $C$ と直線 PQ の交点を求めると

$\begin{cases}x^2+y^2=25\\y=-\cfrac{4}{3}x+\cfrac{25}{6}\end{cases}$

$y=-\cfrac{1}{6}(8x-25)$ とすると

$x^2+\cfrac{1}{36}(8x-25)^2=25$

$36x^2+(8x-25)^2=25\cdot36$

$36x^2+64x^2-16\cdot25x+25^2=25\cdot36$

$100x^2-16\cdot25x+25^2=25\cdot36$

$4x^2-16x+25=36$

$4x^2-16x-11=0$

$x=\cfrac{8\pm\sqrt{64+44}}{4}$

$=\cfrac{8\pm\sqrt{108}}{4}$

$=\cfrac{8\pm6\sqrt{3}}{4}$

$=\cfrac{4\pm3\sqrt{3}}{2}$

・・・フヘホ

第１問，第２問は必答。第３問～第５問はいずれか２問を選択し，解答する。

第１問　問題文

〔1〕　連立方程式

$(\text{＊})\begin{cases}2^{x-2}+\cfrac{1}{2}y=3\\x-\log_{\sqrt{2}} y=2\end{cases}$

を満たす実数 $x$，$y$ を求め，さらに $x+y$ 以下の整数のうちで最大のものを求めよう。

真数の条件により $y > \boxed{\text{ ア }}$ である。ただし，対数 $\log_a b$ に対し，$a$ を底といい，$b$ を真数という。

まず，$z=2^x$ とおくと，(＊)は

$\begin{cases}z+\boxed{\text{ イ }}\space y=\boxed{\text{ ウエ }}\cdots\text{①}\\\log_2 z-\log_{\sqrt{2}} y=2\cdots\text{②}\end{cases}$

次に，$w=\log_{\sqrt{2}} y$ とおくと，$y=(\sqrt{2})^w$ である。この等式において，2 を底とする両辺の対数をとることにより，$w=\boxed{\text{ オ }}\log_2 y$ であることがわかる。したがって，②は

$z=\boxed{\text{ カ }}\space y^{\boxed{\text{キ}}}\cdots$③

と変形できる。

①と③を連立させた方程式を解いて，$y > \boxed{\text{ ア }}$ に注意すると

$y=\cfrac{\boxed{\text{ ク }}}{\boxed{\text{ ケ }}}$，$z=\boxed{\text{ コ }}$

となる。したがって，$x=\log_2 \boxed{\text{ コ }}$ である。

最後に，$x+y=\log_2 \boxed{\text{ コ }}+\cfrac{\boxed{\text{ ク }}}{\boxed{\text{ ケ }}}$ 以下の整数のうちで最大のものを求めよう。

$x=\log_2\boxed{\text{ コ }}$

$\cfrac{n}{2} \leqq\log_2\boxed{\text{ コ }}\leqq\cfrac{n+1}{2}$

を満たす整数 $n$ は $\boxed{\text{ サ }}$ である。したがって，$x+y$ 以下の整数のうちで最大のものは $\boxed{\text{ シ }}$ である。

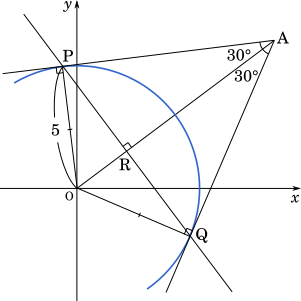
〔2〕　座標平面において，原点 O を中心とする半径 $5$ の円 C と，C の外部にある第 1 象限の点 A を考える。A から C に引いた 2 本の接線の接点を P，Q とする。ただし，P の $x$ 座標が Q の $x$ 座標より小さいとする。∠PAQ=$\cfrac{\pi}{3}$ であり，かつ直線 PQ の傾きが $-\cfrac{4}{3}$ であるとき，点 A の座標と接点 P，Q の $x$ 座標を求めよう。

(1)　円 $C$ の方程式は $x^2+y^2=\boxed{\text{ スセ }}$ である。

(2)　∠OAP=$\cfrac{\pi}{\boxed{\text{ ソ }}}$ であるので，OA=$\boxed{\text{ タチ }}$ である。また，直線 OA と直線 PQ は垂直であるから，直線 OA の傾きは $\cfrac{\boxed{\text{ ツ }}}{\boxed{\text{ テ }}}$ である。よって，A の座標は $(\boxed{\text{ ト }},\boxed{\text{ ナ }})$ である。

(3)　直線 OA と直線 PQ の交点を R とおくと，OR=$\cfrac{\boxed{\text{ ニ }}}{\boxed{\text{ ヌ }}}$ であるので，点 R は線分 OA を $1 :\boxed{\text{ ネ }}$ に内分する。このことを用いると，直線 PQ の方程式は $y=-\cfrac{4}{3}x+\cfrac{\boxed{\text{ ノハ }}}{\boxed{\text{ ヒ }}}$ となることがわかる。

円 $C$ の方程式と直線 PQ の方程式により， P の $x$ 座標と Q の $x$ 座標は，それぞれ

$\cfrac{\boxed{\text{ フ }}-\boxed{\text{ ヘ }}\sqrt{\boxed{\text{ ホ }}}}{2}$，$\cfrac{\boxed{\text{ フ }}+\boxed{\text{ ヘ }}\sqrt{\boxed{\text{ ホ }}}}{2}$

であることがわかる。