【スマホで読む・わかりやすい】センター数学IIB2013追試【解説・正解・問題】

第１問

〔1〕　実数 $x$，$y$ が $x^2+y^2=1$，$y \geqq 0$ を満たすとき，$z=2x^2+4xy-y^2$ を最大にする $x$，$y$ の値とそのときの $z$ の値を求めよう。

$x^2+y^2=1$，$y \geqq 0$ により，$0 \leqq \theta\leqq \pi$ の範囲の $\theta$ を用いて，$x=\cos\theta$，$y=\sin\theta$ とおくことができる。$z$ を $\theta$ を用いて表せば

$z=\cfrac{1}{\boxed{\text{ ア }}}+\cfrac{\boxed{\text{ イ }}\cos 2\theta+\boxed{\text{ ウ }}\sin 2\theta}{2}$

$=\cfrac{1}{\boxed{\text{ ア }}}+\cfrac{\boxed{\text{ エ }}}{2}\sin (2\theta+\alpha)\cdots$①

となる。ただし，$\alpha$ は，鋭角 $\bigg(0 < \alpha < \cfrac{\pi}{2} \bigg)$ で，$\sin \alpha = \cfrac{\boxed{\text{ イ }}}{\boxed{\text{ エ }}}$，$\cos\alpha=\cfrac{\boxed{\text{ ウ }}}{\boxed{\text{ エ }}}$ を満たすものとする。

$2\theta+\alpha$ のとり得る値の範囲が $\alpha\leqq 2\theta+\alpha\leqq 2\pi+\alpha$ であることに注意すると，①により，$2\theta+\alpha=\cfrac{\pi}{\boxed{\text{ オ }}}$ のとき，$z$ は最大値 $\boxed{\text{ カ }}$ をとることがわかる。

$z$ が最大値 $\boxed{\text{ カ }}$ をとるとき，$2\theta=\cfrac{\pi}{\boxed{\text{ オ }}}-\alpha$ であるから，$\cos 2\theta=\boxed{\text{ キ }}$ となる。$\boxed{\text{ キ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ $\cfrac{\sqrt{3}}{2}\sin\alpha+\cfrac{1}{2}\cos\alpha$

① $\cfrac{\sqrt{2}}{2}\sin\alpha+\cfrac{\sqrt{2}}{2}\cos\alpha$

② $\sin\alpha$

③ $-\sin\alpha$

また，$\theta=\cfrac{1}{2}\bigg(\cfrac{\pi}{\boxed{\text{ オ }}}-\alpha\bigg)$ と $0 < \alpha < \cfrac{\pi}{2}$ により，$\cos\theta > 0$ である。
したがって，$z$ が最大値 $\boxed{\text{ カ }}$ をとるとき

$x=\cos\theta=\cfrac{\boxed{\text{ ク }}\sqrt{\boxed{\text{ ケ }}}}{\boxed{\text{ コ }}}$，$y=\sin\theta=\cfrac{\sqrt{\boxed{\text{ サ }}}}{\boxed{\text{ シ }}}$

であることがわかる。

〔2〕　実数 $a$ に対して，座標平面上で，不等式

$x^2-2ax+y^2-4y+a^2 \leqq 0\cdots$②

の表す領域を $A$ とし，連立不等式

$2x+y\leqq 24$，$x\geqq 0$，$y\geqq 0$

の表す領域を $B$ とする。領域 $A$ と領域 $B$ が共通部分をもつとき，その共通部分を $C$ とする。共通部分 $C$ が $a$ の値によりどのように変化するかを調べよう。

(1)　不等式②は

$(x-\boxed{\text{ ス }})^2+(y-\boxed{\text{ セ }})^2 \leqq \boxed{\text{ ソ }}$

と変形できるので，領域 $A$ は，点$(\boxed{\text{ ス }},\boxed{\text{ セ }})$ を中心とする半径 $\boxed{\text{ タ }}$ の円とその内部である。

(2)　点$(\boxed{\text{ ス }},\boxed{\text{ セ }})$ を中心とする半径 $\boxed{\text{ タ }}$ の円と直線 $2x+y=24$ が接する場合，$\boxed{\text{ チ }}$。$\boxed{\text{ チ }}$ に当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪　領域 $A$ と領域 $B$ は共通部分を持たない

①　共通部分 $C$ は，領域 $A$ と一致するか，または 1 点のみからなる

②　共通部分 $C$ は，領域 $B$ と一致するか，または 2 点のみからなる

③　共通部分 $C$ は，領域 $A$ と領域 $B$ の和集合に等しい

(3)　領域 $A$ と領域 $B$ が共通部分をもつような実数 $a$ のとり得る値の範囲は

$\boxed{\text{ ツテ }}\leqq a \leqq \boxed{\text{ トナ }}+\sqrt{\boxed{\text{ ニ }}}$

である。
共通部分 $C$ が領域 $A$ と一致するような実数 $a$ のとり得る値の範囲は

$\boxed{\text{ ヌ }}\leqq a \leqq \boxed{\text{ トナ }}-\sqrt{\boxed{\text{ ニ }}}$

である。
共通部分 $C$ の面積が，領域 $A$ の面積の半分となるのは

$a=\boxed{\text{ ネ }},\boxed{\text{ ノハ }}$

のときである。

解答・解説

ア,イ $2,3$　ウ $4$　エ $5$

オ $2$　カ $3$　キ $2$

ク $2$　ケ $5$　コ $5$

サ $5$　シ $5$　ス,セ,ソ $a,2,4$

タ $2$　チ $1$　ツテ $-2$

トナ $11$　ニ $5$

ヌ $2$　ネ $0$　ノハ $11$

〔1〕

(1)

$x=\cos\theta$，$y=\sin\theta$ を代入すると

$z=2\cos^2\theta+4\sin\theta\cos\theta-\sin^2\theta$

2倍角の公式

$\sin2\theta=2\sin\theta\cos\theta$

$\cos2\theta=\cos^2\theta-\sin^2\theta$

半角の公式

$\cos^2\theta=\cfrac{1+\cos2\theta}{2}$

を用いて

$z=\cos^2\theta+\cos^2\theta-\sin^2\theta+2\cdot2\sin\theta\cos\theta$

$=\cfrac{1+\cos2\theta}{2}+\cos2\theta+2\sin2\theta$

$=\cfrac{1}{2}+\cfrac{3\cos2\theta+4\sin2\theta}{2}$

三角関数の合成を用いて

$z=\cfrac{1}{2}+\cfrac{5}{2}\sin(2\theta+\alpha)\cdots$①

$\alpha\leqq2\theta+\alpha\leqq2\pi+\alpha$ より

$-1\leqq\sin(2\theta+\alpha)\leqq1$

$z$ は $\sin(2\theta+\alpha)=1$ で最大値 $$ となる。

このとき $2\theta+\alpha=\cfrac{\pi}{2}$

式を変形して

$2\theta=\cfrac{\pi}{2}-\alpha$

$\cos2\theta=\cos\bigg(\cfrac{\pi}{2}-\alpha\bigg)$

$\alpha$ は鋭角より

$=\sin\alpha$

また $\sin\alpha=\cfrac{3}{5}$ より

$cos2\theta=\cfrac{3}{5}$

ここで式を変形して半角の公式の形にするとよい。

$1+\cos2\theta=\cfrac{8}{5}$

$\cfrac{1+\cos2\theta}{2}=\cfrac{4}{5}$

$\cos^2\theta=\cfrac{4}{5}$

$\cos\theta=\cfrac{2\sqrt{5}}{5}$

また $\sin^2\theta+\cos^2\theta=1$ を用いて

$\sin^2\theta+\cfrac{4}{5}=1$

$\sin^2\theta=\cfrac{1}{5}$

$\sin\theta=\cfrac{\sqrt{5}}{5}$

〔2〕

(1)

$x^2-2ax+y^2-4y+a^2\leqq0$

平方完成すると

$(x-a)^2-a^2+(y-2)^2-4+a^2\leqq0$

$(x-a)^2+(y-2)^2\leqq4$

領域 $A$ は，点$(a,2)$ を中心とする半径 $2$ の円とその内部である。

(2)

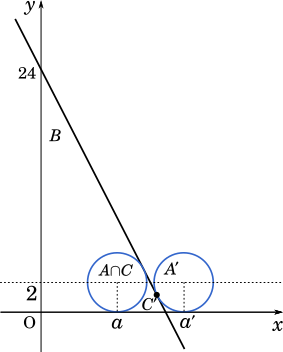
図より点$(a,2)$ を中心とする半径 $2$ の円と直線 $2x+y=24$ が接する場合，共通部分 $C$ は，領域 $A$ と一致するか，または 1 点のみからなる。

(3)

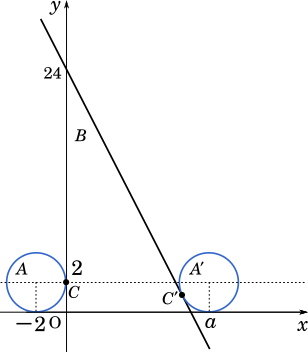
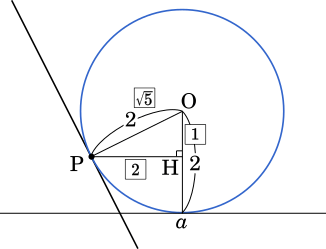
図より PO は 直線 $2x+y=24$ と垂直な直線だから，その傾きは $\cfrac{1}{2}$ であり，PH : HO = $2:1$ となる。

よって，△PHO は$\sqrt{2^2+1^2}=\sqrt{5}$ より，辺の比が $1:2:\sqrt{5}$ の三角形となる。

PH = $2\times\cfrac{2}{\sqrt{5}}=\cfrac{4\sqrt{5}}{5}$

OH = $2\times\cfrac{1}{\sqrt{5}}=\cfrac{2\sqrt{5}}{5}$

これより 点 P の座標は

$\bigg(a-\cfrac{4\sqrt{5}}{5},\space2-\cfrac{2\sqrt{5}}{5}\bigg)$

$\bigg(a-\cfrac{4\sqrt{5}}{5},\space\cfrac{10-2\sqrt{5}}{5}\bigg)$

これを $y=-2x+24$ に代入して

$\cfrac{10-2\sqrt{5}}{5}=-2\bigg(a-\cfrac{4\sqrt{5}}{5}\bigg)+24$

$\cfrac{10-2\sqrt{5}}{5}=-2a+\cfrac{8\sqrt{5}}{5}+24$

$2a=\cfrac{-10+10\sqrt{5}}{5}+24$

$=-2+2\sqrt{5}+24=22+2\sqrt{5}$

$a=11+\sqrt{5}$

したがって領域 $A$ と領域 $B$ が共通部分をもつような実数 $a$ のとり得る値の範囲は

$-2\leqq a\leqq11+\sqrt{5}$

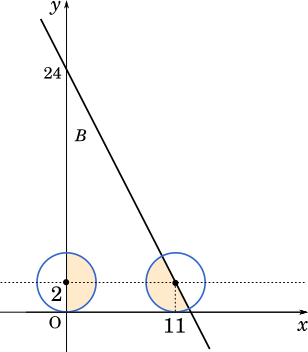
また，共通部分 $C$ の面積が領域 $A$ の面積の半分となる場合を考えると，図より 1 つは $x=0$ のときであることが分かる。また，別の点は

$y=-2x+24$ に $y=2$ を代入して

$2=-2x+24$

$x=11$

したがって $a=0,11$ のときである。