【スマホで読む・わかりやすい】センター数学IIB2013本試【解説・正解・問題】

第１問

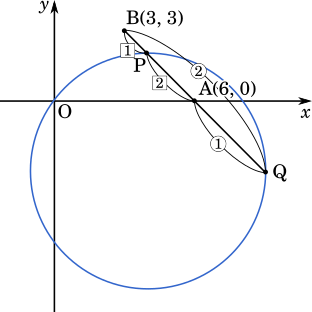
〔1〕　O を原点とする座標平面上に 2 点 A$(6,0)$，B$(3,3)$ をとり，線分 AB を $2:1$ に内分する点を P，$1:2$ に外分する点を Q とする。 3 点 O，P，Q を通る円を $C$ とする。

(1)　P の座標は $(\boxed{\text{ ア }},\boxed{\text{ イ }})$ であり，Q の座標は $(\boxed{\text{ ウ }},\boxed{\text{ エオ }})$ である。

(2)　円 $C$ の方程式を次のように求めよう。線分 OP の中点を通り， OP に垂直な直線の方程式は

$y=\boxed{\text{ カキ }}x+\boxed{\text{ ク }}$

であり，線分 PQ の中点を通り， PQ に垂直な直線の方程式は

$y=x-\boxed{\text{ ケ }}$

である。

これらの 2 直線の交点が円 $C$ の中心であることから，円 $C$ の方程式は

$(x-\boxed{\text{ コ }})^2+(y+\boxed{\text{ サ }})^2=\boxed{\text{ シス }}$

であることがわかる。

(3)　円 $C$ と $x$ 軸の二つの交点のうち，点 O と異なる交点を R とすると，R は線分 OA を $\boxed{\text{ セ }}:1$ に外分する。

〔2〕　連立方程式

$(*)\begin{cases}x+y+z=3\\2^x+2^y+2^z=\cfrac{35}{2}\\\cfrac{1}{2^x}+\cfrac{1}{2^y}+\cfrac{1}{2^x}=\cfrac{49}{16}\end{cases}$

を満たす実数 $x$，$y$，$z$ を求めよう。ただし，$x\leqq y \leqq z$ とする。

$X=2^x$，$Y=2^y$，$Z=2^z$ とおくと，$x\leqq y \leqq z$ により $X\leqq Y \leqq Z$ である。(*)から，$X$，$Y$，$Z$ の関係式

$\begin{cases}XYZ=\boxed{\text{ ソ }}\\X+Y+Z=\cfrac{35}{2}\\XY+YZ+ZX=\cfrac{\boxed{\text{ タチ }}}{\boxed{\text{ ツ }}}\end{cases}$

が得られる。

この関係式を利用すると，$t$ の 3 次式 $(t-X)(t-Y)(t-Z)$ は

$(t-X)(t-Y)(t-Z)=t^3-(X+Y+Z)t^2+(XY+YZ+ZX)t-XYZ$

$=t^3-\cfrac{35}{2}t^2+\cfrac{\boxed{\text{ タチ }}}{\boxed{\text{ ツ }}}t-\boxed{\text{ ソ }}$

$=\bigg(t-\cfrac{1}{2}\bigg)(t-\boxed{\text{ テ }})(t-\boxed{\text{ トナ }})$
となる。したがって，$X\leqq Y \leqq Z$ により

$X=\cfrac{1}{2}$，$Y=\boxed{\text{ テ }}$，$Z=\boxed{\text{ トナ }}$

となり，$\displaystyle x=\log_{\boxed{\text{ニ}}} X$，$\displaystyle y=\log_{\boxed{\text{ニ}}} Y$，$\displaystyle z= \log_{\boxed{\text{ニ}}} Z$ から

$x=\boxed{\text{ ヌネ }}$，$y=\boxed{\text{ ノ }}$，$z=\boxed{\text{ ハ }}$
であることがわかる。

解答・解説

ア,イ $4,2$　ウ,エオ $9,-3$

カキ,ク $-2,5$　ケ $7$

コ,サ $4,3$　シス $25$　セ $4$

ソ $8$　タチ,ツ $49,2$

テ,トナ $1,16$　ニ $2$

ヌネ $-1$　ノ $0$　ハ $4$

〔1〕

(1)

$\text{P}\bigg(\cfrac{6+2\cdot3}{2+1},\space\cfrac{1\cdot0+2\cdot3}{2+1}\bigg)$

$=\text{P}(4,\space2)$

$\text{Q}\bigg(\cfrac{-2\cdot6+1\cdot3}{1-2},\space\cfrac{-2\cdot0+1\cdot3}{1-2}\bigg)$

$=\text{Q}(9,\space-3)$

(2)

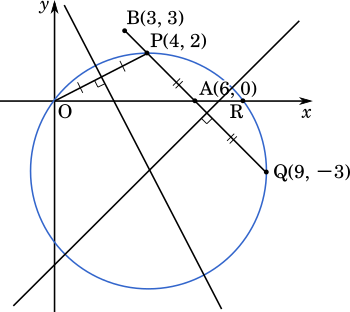
OP の中点の座標は $(2,\space 1)$ であり，またその傾きは $\cfrac{1}{2}$ である。

OP の中点を通り OP と垂直な直線の傾きを $k$ とおくと

$\cfrac{1}{2}k=-1$

$k=-2$

これが $(2,\space1)$ を通るので，直線の式は

$y-1=-2(x-2)$

$y=-2x+5$

PQ の中点を求めると

$\bigg(\cfrac{4+9}{2},\space\cfrac{2-3}{2}\bigg)$

$=\bigg(\cfrac{13}{2},\space-\cfrac{1}{2}\bigg)$

直線 PQ の傾きを求めると

$\cfrac{-3-2}{9-4}=-1$

PQ の中点と垂直な直線の傾きを $\ell$ とすると

$-1\cdot\ell=-1$

$\ell=1$

これが $\bigg(\cfrac{13}{2},\space-\cfrac{1}{2}\bigg)$ を通るので，直線の式は

$y+\cfrac{1}{2}=x-\cfrac{13}{2}$

$y=x-7$

2 直線の交点の座標を求めると

$\begin{cases}y=-2x+5\\y=x-7\end{cases}$

$-2x+5=x-7$

$x=4$

$y=4-7=-3$

弦の垂直二等分線は円の中心を通ることから，この交点は円 $C$ の中心である。よって，円 $C$ の中心の座標は $(4,-3)$

また 円 $C$ は原点を通るので，原点と中心の距離は半径を表す。三平方の定理を用いて

$\sqrt{4^2+(-3)^2}=\sqrt{25}=5$

したがって，円 C の方程式は

$(x-4)^2+(y+3)^2=25$

(3)

R は 円 $C$ の点で $y=0$ だから

$(x-4)^2+3^2=25$

$(x-4)^2=16$

$(x-4)=\pm4$

$x=4\pm4$

$x=0,8$

点 O とは異なる点だから，点 R の座標は $(8,0)$ である。

R は線分 OA を $8:2=4:1$ に外分する。

〔2〕

$XYZ=2^x \times 2^y \times 2^x$

$=2^{x+y+z}$

$=2^3$

$=8$

また，$\cfrac{1}{2^x}+\cfrac{1}{2^y}+\cfrac{1}{2^z}=\cfrac{49}{16}$ を用いて

$\cfrac{1}{X}+\cfrac{1}{Y}+\cfrac{1}{Z}=\cfrac{49}{16}$

$\cfrac{XY+YZ+ZX}{XYZ}=\cfrac{49}{16}$

$\cfrac{XY+YZ+ZX}{8}=\cfrac{49}{16}$

$XY+YZ+ZX=\cfrac{49}{2}$

次に $t^3-\cfrac{35}{2}t^2+\cfrac{49}{2}t-8$ を因数分解する

問題文より，式は $\bigg(t-\cfrac{1}{2}\bigg)$ で割り切れることが分かる。そこで，組立除法を用いて式を割るとよい。

$\begin{aligned}1&&-\cfrac{35}{2}&&\cfrac{49}{2}&&-8&&\space\bigg|\underline{\space\cfrac{1}{2}\space} \\ &&\cfrac{1}{2}&&-\cfrac{17}{2}&&8 \\\hline 1&&-17&&16&& 0\end{aligned}$

よって

$\bigg(t-\cfrac{1}{2}\bigg)(t^2-17+16)$

$=\bigg(t-\cfrac{1}{2}\bigg)(t-1)(t-16)$

となる。

また，$x,y,z$ の値を求めると

$X=2^x$ より

$x=\log_2 X$

が成り立つ。したがって

$x=\log_2\cfrac{1}{2}$ より $x=-1$

同様に $y=\log_2 1$ より $y=0$

$z=\log_2 16$ より $z=4$

が成り立つ。