【数Ⅲ複素数平面】複素数同士が垂直になるとき　複素数と極形式は同じことだと理解する

問題　任意の自然数 nn に対して、複素数 znz_n を zn=(3+i)nz_n=(\sqrt{3}+i)^n で定義する。
複素数平面上で z3nz_{3n}、z3(n+1)z_{3(n+1)}、z3(n+2)z_{3(n+2)} が表す3点をそれぞれA、B、Cとするとき、∠ABCは直角であることを証明せよ。（島根大)

ここでは、複素数同士が垂直になる条件を使っていくよ。

垂直条件が成り立つ仕組み

複素数の垂直
複素数平面上の点A(α)(\alpha)、B(β)(\beta)、C(γ)(\gamma) において、
γ−αβ−α\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}
が純虚数であるとき、AB⊥AC が成り立つ。
式の意味がよく分からないです。

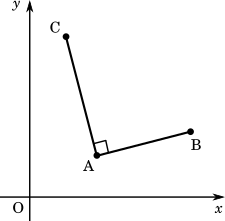
α\alpha を引くことで直線の始点を原点に移動させているんだけど、ベクトルの考え方を使って、AB→=OB→−OA→=β−α\overrightarrow{\text{AB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}=\beta-\alpha って考えてもいい。

あー、そゆこと！

で、複素数って商の公式あったでしょ？

商の公式
α=r1(cos⁡θ1+isin⁡θ1),β=r2(cos⁡θ2+isin⁡θ2)\alpha=r_1(\cos\theta_1+i\sin\theta_1),\beta=r_2(\cos\theta_2+i\sin\theta_2) のとき
αβ=r1r2{cos⁡(θ1−θ2)+isin⁡(θ1−θ2)}\displaystyle \frac{\alpha}{\beta}=\frac{r_1}{r_2}\{\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)\}

つまり、割り算して答えが純虚数なら垂直ってこと。

はい？割り算するのは分かるけど公式は極形式ですよね。

複素数と極形式

話を整理するために単純な例で考えてみようか。点A、Bは以下のようになっていて、三角比の関係から言って∠AOBが30°になるのは分かるよね？


大丈夫です。60°－30°ですね。

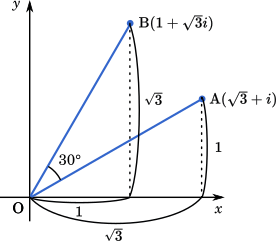
ここで α=3+i\alpha=\sqrt{3}+i、β=1+3i\beta=1+\sqrt{3}i ってして、極形式にした上で割り算するよ。上の三角形は三角比から言ってOAとOBの長さはどっちも2になるのを確認して。

α=2(cos⁡30°+isin⁡30°)\alpha=2(\cos 30\degree+i\sin 30\degree)
β=2(cos⁡60°+isin⁡60°)\beta=2(\cos 60\degree+i\sin 60\degree)
βα=22{cos⁡(60°−30°)+isin⁡(60°−30°)\displaystyle\frac{\beta}{\alpha}=\frac{2}{2}\{\cos(60\degree-30\degree)+i\sin(60\degree-30\degree)
=cos⁡30°+isin⁡30°\displaystyle=\cos 30\degree+i\sin 30\degree
=32+12i\displaystyle=\frac{\sqrt{3}}{2}+\frac{1}{2}i

極形式の結果から、∠AOBが30°だってのが分かる。

疑問だけど、何で割り算すると角度の引き算になるの？

上の公式は加法定理から導かれるもので、あんまり深く考えない方がいいかも。そういうものだと思って。

で、同じ計算を極形式使わないでやってみる。

βα=1+3i3+i\displaystyle\frac{\beta}{\alpha}=\frac{1+\sqrt{3}i}{\sqrt{3}+i}
分母を有理化して
=(1+3i)(3−i)(3+i)(3−i)\displaystyle=\frac{(1+\sqrt{3}i)(\sqrt{3}-i)}{(\sqrt{3}+i)(\sqrt{3}-i)}
=3−i+3i+33+1\displaystyle=\frac{\sqrt{3}-i+3i+\sqrt{3}}{3+1}
=23+2i4\displaystyle=\frac{2\sqrt{3}+2i}{4}
=32+12i\displaystyle=\frac{\sqrt{3}}{2}+\frac{1}{2}i

こんな風に、極形式のときと答えが同じになる。

なりますね。

でも考えてみたら、3+i\sqrt{3}+i を極形式にして 2(cos⁡30°+isin⁡30°)2(\cos 30\degree+i\sin 30\degree) って表すけど、極形式の三角関数を計算したら 3+i\sqrt{3}+i に戻るワケじゃない？ つまり、極形式にすることによって数値が変わるわけじゃなくて、書き方が違うだけで両者はあくまで同じものってことなの。

同じなんだ。

そう。だから複素平面上の問題やるときは、どっちで解くこともできるんだけど、場合によって極形式にした方が計算が楽な時があって、そのときどきでどっちで計算するかを決めることになる。この辺は経験と勘の問題。

メンドイですね。

複素数平面のありがたさを実感してみる

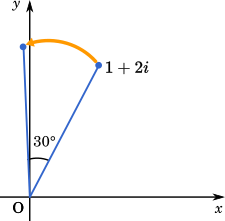
でも、そのおかげで今までの数学ではできなかった計算もできる。たとえば、1+2i1+2i の点を30°回転させた点を求めるとする。

1+2i1+2i って偏角が出せないから、極形式に直せないでしょ？

偏角分からないですね。

でも、偏角分からないでも計算できる。極形式で cos⁡30°+isin⁡30°=32+12i\displaystyle \cos 30\degree+i\sin 30\degree=\frac{\sqrt{3}}{2}+\frac{1}{2}i だから

(1+2i)(32+12i)\displaystyle (1+2i)(\frac{\sqrt{3}}{2}+\frac{1}{2}i)
=32+12i+3i−1\displaystyle =\frac{\sqrt{3}}{2}+\frac{1}{2}i+\sqrt{3}i-1
=3−22+1+232i\displaystyle =\frac{\sqrt{3}-2}{2}+\frac{1+2\sqrt{3}}{2}i

こんな感じで、ちゃんと回転した先の点の位置が分かる。複素数平面って便利でしょ？

今までできなかったのが、できるようになるのはうれしいかもです。

垂直イコール純虚数の意味

今度は90°回転ってのを考える。90°は極形式にするとcos⁡90°+isin⁡90°=0+i=i\cos 90\degree+i\sin 90\degree=0+i=i ってなる。つまり、もとの複素数に 純虚数 ii をかけると90°回転になるの。

純虚数なんですね。

そう、そこ大事。考えてみると分かるけど、00 から 180°180\degree の範囲で言うと、純虚数になる、つまり cos⁡\cos が 00 になるときって90°しかないでしょ？だから純虚数＝90°っていうことになるの。
今回の問題では割り算するんだけど、割り算すると直線同士の偏角が出てくるから、それが純虚数であれば偏角が垂直だって言えることになる。それをふまえて問題を解いていくよ。

公式を用いて偏角を考える

問題　任意の自然数 nn に対して、複素数 znz_n を zn=(3+i)nz_n=(\sqrt{3}+i)^n で定義する。
複素数平面上で z3nz_{3n}、z3(n+1)z_{3(n+1)}、z3(n+2)z_{3(n+2)} が表す3点をそれぞれA、B、Cとするとき、∠ABCは直角であることを証明せよ。（島根大)

さっきの公式から言えば、今回やりたい計算は z3(n+2)−z3(n+1)z3n−z3(n+1)\displaystyle \frac{z_{3(n+2)}-z_{3(n+1)}}{z_{3n}-z_{3(n+1)}} となる。これが純虚数になればオッケー。

計算大変そう。

いきなり公式に代入する前に、それぞれを計算するとよい。

z3n=(3+i)3nz_{3n}=(\sqrt{3}+i)^{3n}

ここは zn=(3+i)nz_n=(\sqrt{3}+i)^n から nn を 3n3n に置きかえただけよ。で、ここから極形式にしてもいいんだけど、そのまま計算してもそれほど大変じゃないから、展開するよ。

={(3+i)3}n=\{(\sqrt{3}+i)^3\}^n
=(33+9i−33−i)n=(3\sqrt{3}+9i-3\sqrt{3}-i)^n
=(8i)n=(8i)^n

よって
z3(n+1)=(3+i)3(n+1)={(3+i)3}n+1=(8i)n+1z_{3(n+1)}=(\sqrt{3}+i)^{3(n+1)}=\{(\sqrt{3}+i)^3\}^{n+1}=(8i)^{n+1}
z3(n+2)=(3+i)3(n+2)={(3+i)3}n+2=(8i)n+2z_{3(n+2)}=(\sqrt{3}+i)^{3(n+2)}=\{(\sqrt{3}+i)^3\}^{n+2}=(8i)^{n+2}

z3(n+2)−z3(n+1)z3n−z3(n+1)=(8i)n+2−(8i)n+1(8i)n−(8i)n+1\displaystyle \frac{z_{3(n+2)}-z_{3(n+1)}}{z_{3n}-z_{3(n+1)}}=\frac{(8i)^{n+2}-(8i)^{n+1}}{(8i)^n-(8i)^{n+1}}
=(8i)n+1(8i−1)(8i)n(1−8i)\displaystyle =\frac{(8i)^{n+1}(8i-1)}{(8i)^n(1-8i)}
=−(8i)n+1(1−8i)(8i)n(1−8i)\displaystyle =\frac{-(8i)^{n+1}(1-8i)}{(8i)^n(1-8i)}
=−8i\displaystyle =-8i

したがって、純虚数であるから∠ABCは直角である。

指数の計算力が求められるから、計算の意味が分からなかったら指数の法則のところに戻ってね。

SNSでシェア

mm参考書 2019-2023