【数ⅡB数列】漸化式:階差数列から一般項を求める
次の数列の一般項を求めよ。
$\displaystyle a_{n+1}=a_n+2n^2+n-\frac{1}{2}$

こういうパターン来たら、まず階差数列を考える。

どうやって求めるの?

階差数列ってのは2つの項の差が何かの数列になってるヤツだから、2項間の差ってのを作るといい。
$a_n$を移項して
$\displaystyle a_{n+1}-a_n=2n^2+n-\frac{1}{2}$

あとはシグマ使って階差の和を求めれば一般項ができる。

どういうこと?

例えば、$a_1$と$a_2$の差を$b_1$ってする。もし、$a_4$を求めたいなら、$a_1+b_1+b_2+b_3$で$a_4$になるでしょ?
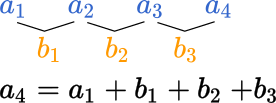

注意しないといけないのは、$a_4$を求めるなら階差数列は$b_3$までの和になる。つまり、第$n$項を求めたいなら階差数列は$n-1$項まで求めることになる。

結果として、こういう公式ができあがる。
$\displaystyle a_n=a_1+\sum_{k=1}^{n-1} b_n$
初項に階差の部分を足していくと求めたい項の値になる。
$\displaystyle a_n=a_1+\sum_{k=1}^{n-1} b_n$
初項に階差の部分を足していくと求めたい項の値になる。
一般項を求めると
$\displaystyle a_n=3+\sum_{k=1}^{n-1} 2k^2+k-\frac{1}{2}$

ここからどう計算するんですか?

公式あったの思い出して。
$\displaystyle \sum_{k=1}^n k=\frac{1}{2}n(n+1)$
$\displaystyle \sum_{k=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
$\displaystyle \sum_{k=1}^n k^2=\frac{1}{6}n(n+1)(2n+1)$
$\displaystyle a_n=3+2\cdot\frac{1}{6}(n-1)n\{2(n-1)+1\}+\frac{1}{2}(n-1)n-\frac{1}{2}(n-1)$

計算が何やってるか分からない。

やってることはこんな感じ。公式の$n$を$n-1$に置き換えていくの。1ずつ減らしていくから、$n$は$n-1$になるし、$n+1$は $1$ 減らして $n$ になる。
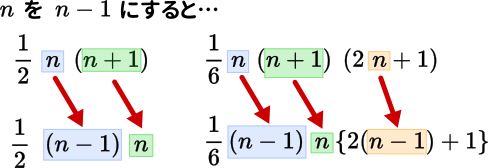
$\displaystyle =3+\frac{1}{3}n(n-1)(2n-2+1)+\frac{1}{2}n(n-1)-\frac{1}{2}(n-1)$
$\displaystyle =3+\frac{1}{3}n(n-1)(2n-1)+\frac{1}{2}n(n-1)-\frac{1}{2}(n-1)$
$\displaystyle =3+\frac{1}{3}(2n^3-3n^2+n)+\frac{1}{2}(n^2-n)-\frac{1}{2}(n-1)$

解答どうしたらいいんですか?

基本的にはなるべく式をシンプルな形に持っていく方向で整理していく。この辺は問題いろいろ解いて模範解答の形に合わせる練習が必要だね。理屈というより経験値の問題だから、練習重ねていくと「こういう形ならオッケー」ってのが見えてくる。
全体を $\displaystyle\frac{1}{6}$ でくくると
$\displaystyle =\frac{1}{6}(18+4n^3-6n^2+2n+3n^2-3n-3n+3)$
$\displaystyle =\frac{1}{6}(4n^3-3n^2-4n+21)$

これで一般項ができたけど、これが $a_1$ でも成り立つことを示しておくのが決まり。
$\displaystyle a_1=\frac{1}{6}(4-3-4+21)=3$
よって、$n=1$ のときにも成り立つ。したがって
$\displaystyle =\frac{1}{6}(4n^3-3n^2-4n+21)$(答え)

最後の$a_1$求める部分って要るんですか?

まあ、お約束事だからってのもあるけど、あくまでシグマの計算のところってのは初項に階差部分を足していくから $n\geqq 2$ での話なの。だからこの式って $a_1$ のときには成り立たない可能性がある。だから確認が必要。

メンドイですね。

そうね。確かにメンドイかも。でもこの問題を通じて数学的に正しいってことを証明するための手続きを身につけてね。これは数学に限らず科学的なものの考え方を身につける上で大事なポイントでもあるの。がんばって。
SNSでシェア