【スマホで読む・わかりやすい】共通テスト試行H29年度数学IA【解説・正解・問題】
第1問
〔 1 〕 数学の授業で, 2 次関数 $y = ax^2 + bx + c$ についてコンピュータのグラフ表示ソフトを用いて考察している。
このソフトでは、図 1 の画面上の $\boxed{\text{ A }}$、$\boxed{\text{ B }}$、$\boxed{\text{ C }}$ にそれぞれ係数 $a,b,c$ の値を入力すると、その値に応じたグラフが表示される。さらに,$\boxed{\text{ A }}$、$\boxed{\text{ B }}$、$\boxed{\text{ C }}$ それぞれの下にある●を左に動かすと係数の値が減少し,右に動かすと係数の値が増加するようになっており,値の変化に応じて 2 次関数のグラフが座標平面上を動く仕組みになっている。
また,座標平面は $x$ 軸,$y$ 軸によって四つの部分に分けられる。これらの各部分を「象限」といい,右の図のように,それぞれを「第 1 象限」「第 2 象限」「第 3 象限」「第 4 象限」という。ただし,座標軸上の点は,どの象限にも属さないものとする。
このとき,次の問いに答えよ。

〔1〕(1)
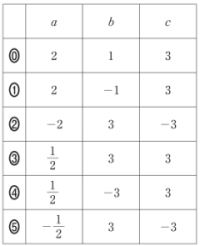
はじめに,図 1 の画面のように,頂点が第 3 象限にあるグラフが表示された。このときの $a,b,c$ の値の組合せとして最も適当なものを,次の ⓪ 〜 ⑤ のうちから一つ選べ。 $\boxed{\text{ ア }}$
正解と解説
$\boxed{\text{ ア }}$ ③
式を平方完成すると
$y=ax^2+bx+c$
$\displaystyle=a\left(x^2+\frac{b}{a}x\right)+c$
$\displaystyle=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2}{4a}+c$
グラフの頂点は第3象限にあるので
$\displaystyle-\frac{b}{2a}<0,-\frac{b^2}{4a}+c<0$
また、下に凸のグラフだから、$a>0$
この条件をそれぞれ当てはめてみると
⓪ $\displaystyle-\frac{1^2}{4\cdot2}+3=\frac{23}{8}>0\cdots$不適
① $\displaystyle-\frac{-1}{2}=\frac{1}{2}>0\cdots$不適
② $a<0\cdots$不適
③ $\displaystyle-\frac{3}{2\cdot\frac{1}{2}}=3<0$
$\displaystyle-\frac{3^2}{4\cdot\frac{1}{2}}+3=-\frac{3}{2}<0\cdots$適する
④ $\displaystyle-\frac{-3}{2\cdot\frac{1}{2}}=3>0\cdots$不適
⑤ $a<0\cdots$不適
〔1〕(2)
次に,$a,b$ の値を(1)の値のまま変えずに,$c$ の値だけを変化させた。このときの頂点の移動について正しく述べたものを,次の ⓪ 〜 ④ のうちから一つ選べ。 $\boxed{\text{ イ }}$
⓪ 最初の位置から移動しない。
① $x$ 軸方向に移動する。
② $y$ 軸方向に移動する。
③ 原点を中心として回転移動する。
正解と解説
$\boxed{\text{ イ }}$ ②
頂点の座標は$\displaystyle\left(-\frac{b}{2a},-\frac{b^2}{4a}+c\right)$だから、$c$の値を変化させると、$y$軸方向にのみ移動する。
〔1〕(3)
また,b,c の値を(1)の値のまま変えずに,$a$ の値だけをグラフが下に凸の状態を維持するように変化させた。このとき,頂点は,$\displaystyle a=\frac{b^2}{4c}$ のときは$\boxed{\text{ ウ }}$ にあり,それ以外のときは $\boxed{\text{ エ }}$ を移動した。$\boxed{\text{ ウ }}$,$\boxed{\text{ エ }}$ に当てはまるものを,次の ⓪ 〜 ⑧ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ 原点 ① $x$ 軸上 ② $y$ 軸上
③ 第 3 象限のみ ④ 第 1 象限と第 3 象限
⑤ 第 2 象限と第 3 象限 ⑥ 第 3 象限と第 4 象限
⑦ 第 2 象限と第 3 象限と第 4 象限 ⑧ すべての象限
正解と解説
$\boxed{\text{ ウ }}$,$\boxed{\text{ エ }}$ ①、⑤
$b=3,c=3$ とすると、頂点の座標は
$\displaystyle\left(-\frac{3}{2a},-\frac{9}{4a}+3\right)$
このとき、$\displaystyle a=\frac{b^2}{4c}=\frac{3^2}{4\cdot 3}=\frac{3}{4}$ とおくと、頂点の座標は
$\displaystyle\left(-\frac{3}{2\cdot\frac{3}{4}},-\frac{9}{4\cdot\frac{3}{4}}+3\right)$
$\displaystyle=(-6,0)$
となり、$x$ 軸上にある。
また、グラフが下に凸であるから $a>0$ より、頂点の座標を考えると
$x$ 座標は $\displaystyle -\frac{3}{2a}$ より常に負の値をとる。
$y$ 座標は $\displaystyle -\frac{9}{4a}+3$ より正の値、負の値のどちらもとる。
よって、頂点は第2象限と第3象限にある。
〔1〕(4)
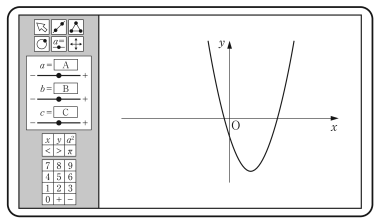
最初の $a,b,c$ の値を変更して,下の図 2 のようなグラフを表示させた。このとき,$a,c$ の値をこのまま変えずに,$b$ の値だけを変化させても,頂点は第 1 象限および第 2 象限には移動しなかった。
その理由を,頂点の $y$ 座標についての不等式を用いて説明せよ。解答は,解答欄 $\boxed{\text{ (あ) }}$ に記述せよ。
正解と解説
$\boxed{\text{ (あ) }}$ $a>0,c<0$ であることにより、頂点の $y$ 座標について、つねに $\displaystyle -\frac{b^2-4ac}{4a}<0$ となるから。
$b$ の値が変化するので、それ以外の $a,c$ の条件を考えるとよい。
グラフが下に凸だから $a>0$
また、グラフを見ると $y$ 軸の負の側を通っていることが分かる。
$y=ax^2+bx+c$ において、$x=0$ とすると $y=c$ となり、$c<0$ である。
ここで、頂点の $y$ 座標 $\displaystyle-\frac{b^2}{4a}+c$ を考える。
$a$ が常に正の値、$b^2$ は 2乗しているから常に正の値、$c$ が常に負の値だとすると、式全体としては常に負の値をとることになる。
〔 2 〕 以下の問題では,△ABC に対して,∠A,∠B,∠C の大きさをそれぞれ $A$,$B$,$C$ で表すものとする。
ある日,太郎さんと花子さんのクラスでは,数学の授業で先生から次のような宿題が出された。
宿題 △ABC において A = 60° であるとする。このとき,
$X=4\cos^2 B+4\sin^2 C-4\sqrt{3}\cos B\sin C$
の値について調べなさい。
放課後,太郎さんと花子さんは出された宿題について会話をした。二人の会話を読んで,下の問いに答えよ。
太郎: $A$ は 60° だけど,$B$ も $C$ も分からないから,方針が立たないよ。
花子: まずは,具体的に一つ例を作って考えてみようよ。もし $B = 90\degree$ であるとすると,$\cos B = \boxed{\text{ オ }}$,$\sin C = \boxed{\text{ カ }}$ だね。だから,この場合の $X$ の値を計算すると $1$ になるね。
〔2〕(1)
$\boxed{\text{ オ }}$,$\boxed{\text{ カ }}$ に当てはまるものを,次の ⓪ 〜 ⑧ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $0$ ① $1$ ② $-1$ ③ $\displaystyle\frac{1}{2}$ ④$\displaystyle\frac{\sqrt{2}}{2}$
⑤ $\displaystyle\frac{\sqrt{3}}{2}$ ⑥ $\displaystyle-\frac{1}{2}$ ⑦ $\displaystyle -\frac{\sqrt{2}}{2}$ ⑧ $\displaystyle -\frac{\sqrt{3}}{2}$
正解と解説
$\boxed{\text{ オ }}$,$\boxed{\text{ カ }}$ ⓪、③
$A=60\degree,B=90\degree$ とすると $C=30\degree$ である。
よって
$\displaystyle\cos B=\cos 90\degree=0$
$\displaystyle\sin C=\sin 30\degree=\frac{1}{2}$
太郎: $B = 13\degree$ にしてみよう。数学の教科書に三角比の表があるから,それを見ると,$\cos B = 0.9744$ で,$\sin C$ は……あれっ? 表には $0\degree$ から $90\degree$ までの三角比の値しか載っていないから分からないね。
花子: そういうときは,$\boxed{\text{ キ }}$ という関係を利用したらいいよ。この関係を使うと,教科書の三角比の表から $\sin C = \boxed{\text{ ク }}$ だと分かるよ。
太郎: じゃあ,この場合の $X$ の値を電卓を使って計算してみよう。 $\sqrt{3}$ は $1.732$ として計算すると……あれっ? ぴったりにはならなかった
けど,小数第 $4$ 位を四捨五入すると,$X$ は $1.000$ になったよ!
(a)これで,$A = 60\degree$,$B = 13\degree$ のときに $X = 1$ になることが証明できたことになるね。さらに,(b)「$A = 60\degree$ ならば $X = 1$」という命題が真であると証明できたね。
花子:本当にそうなのかな?
〔2〕(2)
$\boxed{\text{ キ }}$,$\boxed{\text{ ク }}$ に当てはまる最も適当なものを,次の各解答群のうちから一つずつ選べ。
$\boxed{\text{ キ }}$ の解答群:
⓪ $\sin(90\degree-\theta)=\sin\theta$ ① $\sin(90\degree-\theta)=-\sin\theta$
② $\sin(90\degree-\theta)=\cos\theta$ ③ $\sin(90\degree-\theta)=-\cos\theta$
④ $\sin(180\degree-\theta)=\sin\theta$ ⑤ $\sin(180\degree-\theta)=-\sin\theta$
⑥ $\sin(180\degree-\theta)=\cos\theta$ ⑦ $\sin(180\degree-\theta)=-\sin\theta$
$\boxed{\text{ ク }}$ の解答群:
⓪ $-3.2709$ ① $-0.9563$ ② $0.9563$ ③ $3.2709$
正解と解説
$\boxed{\text{ キ }}$、$\boxed{\text{ ク }}$ ④、②
$C$ を求めると $C=180-(60+13)=73\degree$
角度が $90\degree$ を超える場合には $\sin(180\degree-\theta)=\sin\theta$ の関係を使うとよい。
よって、$\sin(180\degree-107\degree)=\sin 73\degree$ となる。
角度が $0\degree$ から $90\degree$ のとき $\sin$ の値は $0$ から $1$ の間の値をとるので、消去法で $0.9563$ であることが分かる。
〔2〕(3)
太郎さんが言った下線部(a),(b)について,その正誤の組合せとして正しいものを,次の ⓪ 〜 ③ のうちから一つ選べ。 $\boxed{\text{ ケ }}$
⓪ 下線部(a),(b)ともに正しい。
① 下線部(a)は正しいが,(b)は誤りである。
② 下線部(a)は誤りであるが,(b)は正しい。
③ 下線部(a),(b)ともに誤りである。
正解と解説
四捨五入によって得られた値で $X=1$ であると言うことはできない。したがって、「$A=60\degree$ならば$X=1$」という命題が真であるかどうかも判断できない。
花子: $A = 60\degree$ ならば $X = 1$ となるかどうかを,数式を使って考えてみようよ。△ABC の外接円の半径を $R$ とするね。すると,$A = 60\degree$ だから,BC $= \sqrt{\boxed{\text{ コ }}}R$ になるね。
太郎:AB = $\boxed{\text{ サ }}$,AC = $\boxed{\text{ シ }}$ になるよ。
〔2〕(4)
$\boxed{\text{ コ }}$ に当てはまる数を答えよ。また,$\boxed{\text{ サ }}$,$\boxed{\text{ シ }}$ に当てはまるものを,次の ⓪ 〜 ⑦ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $R\sin B$ ① $2R\sin B$ ② $R\cos B$ ③ $2R\cos B$
④ $R\sin C$ ⑤ $2R\sin C$ ⑥ $R\cos C$ ⑦ $2R\cos C$
正解と解説
$\boxed{\text{ コ }}$,$\boxed{\text{ サ }}$,$\boxed{\text{ シ }}$ $3$、⑤、①
正弦定理より
$\displaystyle\frac{\text{BC}}{\sin A}=2R$
$BC=\sin a\times 2R$
$=\sin 60\degree\times 2R$
$=\sqrt{3}R$
また
$\displaystyle\frac{\text{AB}}{\sin C}=2R$
$AB=2R\sin C$
$\displaystyle\frac{\text{AC}}{\sin B}=2R$
$AC=2R\sin B$
花子:まず,$B$ が鋭角の場合を考えてみたよ。
<花子さんのノート>
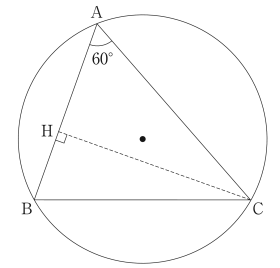
点 C から直線 AB に垂線 CH を引くと
AH = AC$\cos 60\degree$①
BH = BC$\cos B$②
である。AB を AH,BH を用いて表すと
AB = AH + BH③ であるから
AB = $\boxed{\text{ ス }}\sin B + \boxed{\text{ セ }}\cos B$④が得られる。
太郎: さっき,AB = $\boxed{\text{ サ }}$ と求めたから,④の式とあわせると, $X = 1$ となることが証明できたよ。
花子: B が直角のときは,すでに $X = 1$ となることを計算したね。
(c)$B$ が鈍角のときは,証明を少し変えれば,やはり $X = 1$ であることが示せるね。
〔2〕(5)
$\boxed{\text{ ス }}$,$\boxed{\text{ セ }}$ に当てはまるものを,次の ⓪ 〜 ⑧ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $\displaystyle\frac{1}{2}R$ ① $\displaystyle\frac{\sqrt{2}}{2}R$ ② $\displaystyle\frac{\sqrt{3}}{2}R$ ③ $R$ ④ $\sqrt{2}R$
⑤ $\sqrt{3}R$ ⑥ $2R$ ⑦ $2\sqrt{2}R$ ⑧ $2\sqrt{3}R$
正解と解説
$\boxed{\text{ ス }}$,$\boxed{\text{ セ }}$ ③、⑤
$\text{AH}=\text{AC}\cos 60\degree$
$\displaystyle=\text{AC}\cdot\frac{1}{2}$
$\displaystyle=2R\sin B\cdot\frac{1}{2}$
$=R\sin B$
$\text{BH}=\text{BC}\cos B$
$=\sqrt{3}R\cos B$
〔2〕(6)
下線部(c)について,$B$ が鈍角のときには下線部①〜③の式のうち修正が必要なものがある。修正が必要な番号についてのみ,修正した式をそれぞれ答えよ。解答は,解答欄$\boxed{\text{ い }}$に記述せよ。
正解と解説
$\boxed{\text{ い }}$ ② $\text{BH}=-\text{BC}\cos B$、③ $\text{AB}=\text{AH}-\text{BH}$ (①は修正の必要なし)
$B$ が鋭角のとき、図は下のようになる。
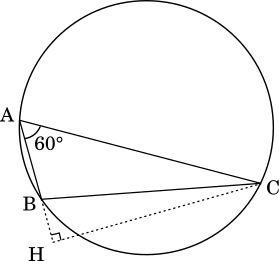
$\cos(180\degree-\theta)=-\cos\theta$ の関係より
$\text{BH}=-\text{BC}\cos B$
$\text{AB}=\text{AH}-\text{BH}$
花子: 今まではずっと $A = 60\degree$ の場合を考えてきたんだけど,$A = 120\degree$ で $B = 30\degree$ の場合を考えてみたよ。$\sin B$ と $\cos C$ の値を求めて,$X$ の値を計算したら,この場合にも $1$ になったんだよね。
太郎: わっ,本当だ。計算してみたら $X$ の値は $1$ になるね。
〔2〕(7)
△ABC について,次の条件 $p$,$q$ を考える。
$p:A = 60\degree$
$q: 4\cos^2 B+4\sin^2 C-4\sqrt{3}\cos B\sin C=1$
これまでの太郎さんと花子さんが行った考察をもとに,正しいと判断できるものを,次の ⓪ 〜 ③ のうちから一つ選べ。$\boxed{\text{ ソ }}$
⓪ $p$ は $q$ であるための必要十分条件である。
① $p$ は $q$ であるための必要条件であるが,十分条件でない。
② $p$ は $q$ であるための十分条件であるが,必要条件でない。
③ $p$ は $q$ であるための必要条件でも十分条件でもない。
正解と解説
$\boxed{\text{ ソ }}$ ②
これまでの考察より、$p\implies q$ は真であると言えるが、$A=120\degree$ の時にも $X=1$ が成り立つと言っているので、$q\implies p$ は偽である。したがって、$p$ は $q$ であるための十分条件であるが、必要条件でない。
SNSでシェア