【高校数学・積分】どうして積分すると面積になるのか? ざっくりイメージで理解する

積分で関数を積分したら面積になるって習ったんですけど。

はいはい。

教科書に説明のってるけど全然意味が分からないです。

うん、まあ、数学的にちゃんと説明しようとすればああいう説明になるから仕方ないね。そういうものだと思って納得したら?

でも、なんかすっきりしないです。

だったら、ざっくりしたイメージを説明してみるね。
中学理科の実験にさかのぼる
中学のときに理科で次のような装置を用いた実験を行いました。台車に記録テープを取り付けて、その台車を加速させます。そしてテープを、たとえば0.1秒ごとに切って並べていきます。



テープの長さは 0.1 秒ごとの移動距離、つまり速さを表している。

どんどん速くなってますね。

そうそう。で、今回はこれを使って考えてみる。
1秒ごとの移動距離を合計すると全体の移動距離になる
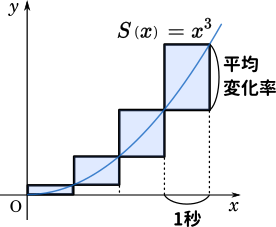
ここでいったん $S(x)=x^3$ という関数を作ります。この関数が 0 秒から $x$ 秒までの移動距離を表していると考えて下さい。そして上と同じように実験します。ここでは1 秒ごとに切ったテープを並べてみます。
テープの長さがそれぞれ、微分で習った平均変化率を表しています。ここでは平均変化率は 1 秒ごとの移動距離になっています。
微分では、この 1 秒を 0.1 秒、0.01 秒、0.001 秒…とひたすら細かく区切っていくことで平均変化率が微分係数(接線の傾き)に近づいていくという考え方でした。

今回はざっくりイメージでいくから、テープの長さと微分した値(微分係数)はほぼ同じものって考えてね。

微分して $y=3x^2$ ですね。

そうそう。それがテープの長さ。たとえば 4 秒のときのテープの長さは $3\times4^2=48$ だよね。
そして、テープ全体でスタートから 4 秒までの移動距離の合計になります。
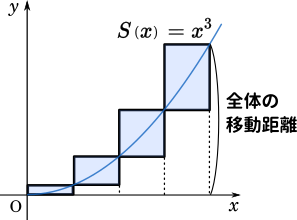

微分した値を積み上げたら、$x^3$ の値になる。
移動距離の合計=面積
今度は、テープを下に移動します。
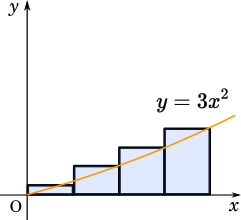

テープの長さは微分した値ってことだったから、このグラフは $x^3$ を微分した $y=3x^2$ のグラフだってことになる。
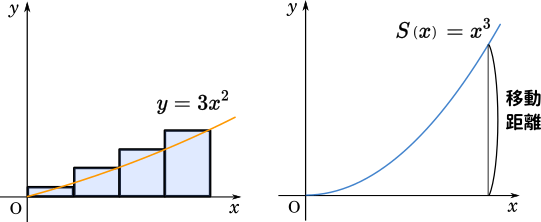
試しにテープの面積を計算してみましょう。テープの縦の長さはそれぞれ $3\times1^2=3$、$3\times2^2=12$、$3\times3^2=27$、$3\times4^2=48$です。また、横幅を $1$ とすると、面積は $1\times(3+12+27+48)=90$ です。
この値が $x^3$ と一致するか確認しましょう。$x=4$ のとき $x^3=4^3=64$ です。

一致しませんよ。

残念ながら区切り方がざっくりすぎて誤差が大きいの。テープの切り方をもっと細かくすれば、$x^3$ の値に近づいていく。
まとめ
今回の実験でつかんでほしいポイントは、
① ある関数を微分した値を積み重ねると、もとの関数に戻る。
② 微分した値を積み重ねたものは面積になる。
③ よって、関数を積分したものは面積を表す。
② 微分した値を積み重ねたものは面積になる。
③ よって、関数を積分したものは面積を表す。
ということです。この3つの関係はイコールで結ぶことができます。

んー、分かったような分からないような。

難しいよね。移動距離を積み上げていくことが積分であり、それが面積であるっていうイメージをつかんでね。
SNSでシェア