【数A場合の数】最短経路の求め方 どうしてCを使うの?
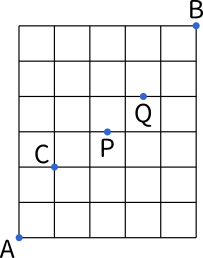
右の図のように、道路が碁盤の目のようになった街がある。地点 A から地点 B までの長さが最短の道を行くとき、次の場合は何通りの道順があるか。(東北大)
(1) 地点 C を通る。
(2) 地点 P は通らない。
(3) 地点 P 、および地点 Q は通らない。

Cを用いて場合の数を求める
まずは (1) から。
地点 C を通るので、経路としては A → C → B ということになります。まずは A → C と C → B に分けて考えましょう。
A → C の経路は、矢印で表すと →↑↑ 、↑→↑、↑↑→ の 3 通りがあります。
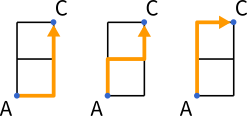

これを式で表すと $_3C_1$ となります。

→↑↑ 、↑→↑、↑↑→ は、言いかえれば → が何番目にくるか、ということです。→ が 1 番目のとき、2番目のとき、3番目のときがあります。
つまり、こう考えてみましょう。袋の中に $\boxed{1}$ ~ $\boxed{3}$ のカードが入っていて、そこから 1 枚のカードを引きます。そしてそれが → が何番目にくるかを表しているとします。
例えばカードを引いて $\boxed{2}$ が出たとすると、→ は 2 番目にくる。つまり、↑→↑ のことです。
3 つから 1 つを取る組み合わせなので $_3C_1$ になるということです。
$_3C_1=3$
次に C → B の経路を考えます。
C → B は →→→→↑↑↑↑ となります。
今度は、$\boxed{1}$ ~ $\boxed{8}$ のカードから、→ が何番目になるかを表したカードを 4 枚ひくと考えます。
例えば、8 枚のカードから 4 枚をひいて、$\boxed{1}$、$\boxed{2}$、$\boxed{5}$、$\boxed{7}$ だったとします。それは →→↑↑→↑→↑ ということになります。


$\displaystyle _8C_4=\frac{8\cdot7\cdot6\cdot5}{4\cdot3\cdot2\cdot1}=70$
こうして、A → C は 3 通り、C → B は 70 通りなので
$3\times70=210$ 通り(答え)
余事象から考える
(2) に進みます。地点 P を通らないというのは、反対に考えて全ての経路から地点 P を通る場合をひくことで求められます。全ての経路を全事象と言います。
全事象は A → B の経路全てということなので、→→→→→↑↑↑↑↑↑ の組み合わせです。
上でやったように、これは 11 枚のカードから → が何番目にくるかを示したカードを 5 枚ひけばよいことになります。よって
$_{11}C_5=462$ 通り
また、P を通る組み合わせは A → P → B の経路です

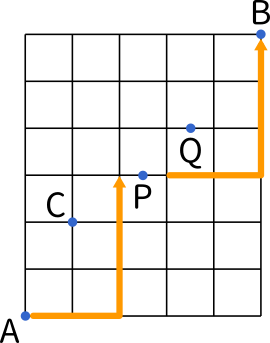

A → P
→→↑↑↑
$_5C_2=10$
P → B
→→↑↑↑
$_5C_2=10$
よって A → P → B の組み合わせは
$10\times10=100$
P を通らない場合は、(全事象)ー(Pを通る場合) だから
$462-100=362$ 通り(答え)
和集合の要素の個数を考える
(3) に進みます。
地点 P、および地点 Q を通らない場合というのは少し注意が必要です。
余事象で考えるのですが、全事象から地点 P かつ Q を通る場合をひけばよい、とはなりません。




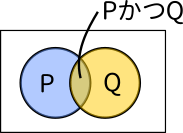
そして P の場合と Q の場合 を数えるとき、P かつ Q の部分が重なっています。P の場合+Q の場合 の計算をするとこの部分で 2 度数えてしまうことになるので、1 回分をひくことで帳尻合わせをします。
$$n(A\cup B)=n(A)+n(B)-n(A\cap B)$$
従って作る式は
全事象ー(Pを通る+Qを通るーPかつQを通る)
となります。
まず、P を通る場合は (2) で 100 通りであることが分かっています。
次に Q を通る場合の経路は A → Q → B です。
A → Q
→→→↑↑↑↑
$_7C_3=35$ 通り
Q → B
→↑↑
$_3C_1=3$ 通り
よって $35\times 3=105$ 通り
そして、P と Q の両方を通る場合を考えます。
経路は A → P → Q → B となります。
A → P
$_5C_2=10$ 通り
P → Q
(P の右側)→(Q の左側)なので $1$ 通り。
Q → B
$_3C_1=3$ 通り
よって $10\times 1\times 3=30$ 通り
これをまとめます。全事象は (2) で求めていて、$462$ 通りでした。
したがって
$462-(100+105-30)=287$ 通り(答え)
SNSでシェア