【数A図形の性質】三角形内の内分点をチェバ・メネラウスを使って求める(九州大)
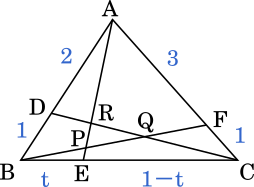
$t$ を $0<t<1$ を満たす実数とする。面積が $1$ である三角形 ABC において、辺 AB, BC, CA をそれぞれ $2:1,t:1-t,1:3$ に内分する点を D,E,F とする。また、AE と BF, BF と CD,CD と AE の交点をそれぞれ P,Q,R とする。このとき以下の問いに答えよ。(九州大2016)
(1) 3 直線 AE,BF,CD が 1 点で交わるときの $t$ の値 $t_0$ を求めよ。
以下、$t$ は $0<t<t_0$ を満たすものとする。
(2) AP$=k$AE, CR$=\ell$CD を満たす実数 $k,\ell$ をそれぞれ求めよ。
(3) 三角形 BCQ の面積を求めよ。
(4) 三角形 PQR の面積を求めよ。

チェバ・メネラウスの定理
三角形の各頂点を通る直線について、次の定理が成り立ちます。
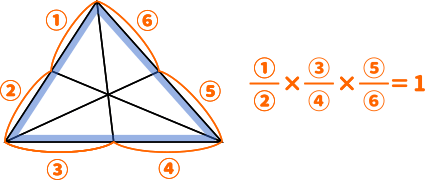
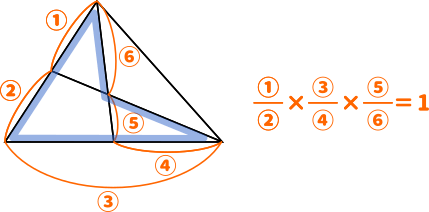
それぞれ注意点があります。
チェバが使えない場合

メネラウスが使えない場合

以上の点に注意して、チェバ・メネラウスの定理が使えるかどうか判断しましょう。
チェバの定理を使う
(1) から解いていきましょう。直線が 1 点で交わるということは図で表すとこのようになります。
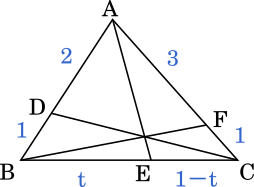

チェバの定理より
$\displaystyle\frac{2}{1}\times\frac{t}{1-t}\times\frac{1}{3}=1$
$\displaystyle\frac{t}{1-t}=\frac{3}{2}$
$2t=3(1-t)$
$2t=3-3t$
$5t=3$
$\displaystyle t=\frac{3}{5}$
よって $\displaystyle t_0=\frac{3}{5}$(答え)
メネラウスの定理を使う
(2) に進みます。
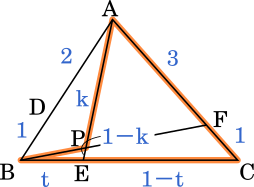
AP$=k$AE の $k$ を求めましょう。

メネラウスの定理より、点 A からスタートして
$\displaystyle \frac{3}{1}\times\frac{1}{1-t}\times\frac{1-k}{k}=1$
$\displaystyle k=\frac{3}{t+3}$(答え)
次に CR$=\ell$CD から $\ell$ を求めます。
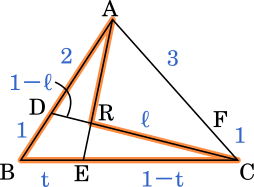


点 C からスタートして
$\displaystyle \frac{1-t}{t}\times\frac{3}{2}\times\frac{1-\ell}{\ell}=1$
$\displaystyle \ell=\frac{3t-3}{t-3}$(答え)
メネラウスの定理を使って面積を求める
(3) に進みます。
点 Q が出てくるので、同様に BQ$=m$BF として $m$ を求めておきましょう。
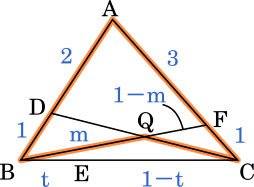


点 B をスタート地点にして
$\displaystyle \frac{1}{2}\times\frac{4}{1}\times\frac{1-m}{m}=1$
$\displaystyle m=\frac{2}{3}$
よって、BQ : QF = 2 : 1 ということが分かります。
あとは底辺の比で三角形の面積を分割していきましょう。
△BCF $\displaystyle =1\times\frac{1}{4}$
△BCQ $=$ △BCF $\displaystyle\times\frac{2}{3}$
従って
△BCQ $\displaystyle =1\times\frac{1}{4}\times\frac{2}{3}=\frac{1}{6}$(答え)
三角形の面積を引き算する
(4) に進みます。
考え方としては、三角形全体の面積から △PQR の周りにある 3 つの三角形の面積を引くことで求めます。
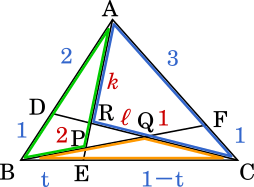
△BCQ の面積は (3) で求めたので、次に △CAR を求めます。△BCQ を求めたときと同様に
△CAR $\displaystyle =1\times\frac{2}{3}\times\ell$
$\displaystyle =\frac{2}{3}\times\frac{3t-3}{t-3}=\frac{2t-2}{t-3}$
また、△ABP を求めると
△ABP $\displaystyle =1\times t\times k=t\times\frac{3t-3}{t-3}=\frac{2t-2}{t-3}$
よって
△PQR $\displaystyle =1-\frac{1}{6}-\frac{2t-2}{t-3}-\frac{3t}{t+3}$

△PQR $\displaystyle =\frac{-25t^2+30t-9}{6(t+3)(t-3)}$(答え)
SNSでシェア