【数Ⅲ複素数平面】点Z全体が円になる問題（国公立基本レベル）

このページでマスターしたいこと：絶対値の扱い方、絶対値＝距離のルール、z全体が円になる式、円の接線から偏角の最大値を求める方法

---

複素数平面上で、等式 $\displaystyle\left|\frac{z-2-2i}{1-i}\right|=1$ を満たす点 $z$ 全体が描く図形を $C$ とする。ただし、$i$ は虚数単位である。以下の各問に答えよ。（茨城大）
(1) 図形 $C$ を複素数平面上に図示せよ。
(2) $z$ が $C$ 上を動くとき、$|z|$ の最大値 $M$ とそのときの $z$ の値を求めよ。ただし、$z$ の値は $\sin,\cos$ を用いずに答えること。
(3) $z$ の偏角 $\arg z$ を $0\text{≦}\arg z<2\pi$の範囲で考える。$z$ が $C$ 上を動くとき、$\arg z$ の最大値 $m$ とそのときの $z$ の値を求めよ。ただし、$z$ の値は $\sin,\cos$ を用いずに答えること。

---

z 全体が表す図形を示す

分数の絶対値は上下で分割することができます。よって

$\displaystyle\left|\frac{z-2-2i}{1-i}\right|=1\\\displaystyle\frac{|z-2-2i|}{|1-i|}=1\\|z-2-2i|=|1-i|$

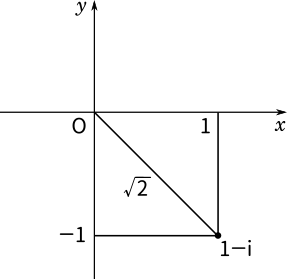
ここで $|1-i|$ をグラフで表すとこのようになります。原点から $1-i$ までの距離は$\sqrt{2}$ になるので、$|1-i|=\sqrt{2}$ です。よって

$|z-2-2i|=\sqrt{2}$

そして、この式は中心が $2+2i$ で半径 $\sqrt{2}$ の円であることを表しています。

（答え）

|Z|の最大値

次に $|z|$ の最大値は、円上で原点から最も離れた点のことです。この点Mをグラフで表すとこのようになります。

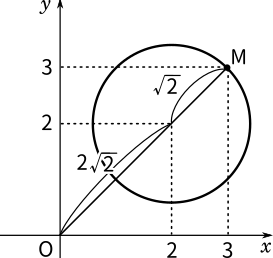
よって、$M=2\sqrt{2}+\sqrt{2}=3\sqrt{2},z=3+3i$（答え）

偏角の最大値

最後(3)です。$\arg$ とは偏角のことでした。偏角が最大になる場合をグラフで表すとこのようになります。

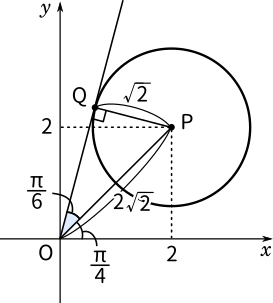
直角三角形ができるので三角形OPQとして、原点OからQまでの距離 $|z|$ を三平方の定理を使って表すと
$|z|=\sqrt{(2\sqrt{2})^2-(\sqrt{2})^2}=\sqrt{6}$
となります。この直角三角形は辺の比が $1:2:\sqrt{3}$ になるのでグラフで青色で示した部分の角度は $\displaystyle\frac{\pi}{6}$ であることが分かります。よって偏角の最大値は
$\displaystyle m=\frac{\pi}{4}+\frac{\pi}{6}=\frac{5}{12}\pi$

（答え）