【数Ⅲ積分】円柱を斜めに切った立体の体積(2)　四角形の積分を用いる・底面が楕円

このページでマスターしたいこと：楕円の方程式から面積を求める、cosによる置換、半角の公式、四角形の面積を積分して円柱を斜めに切った立体の体積を求める

---

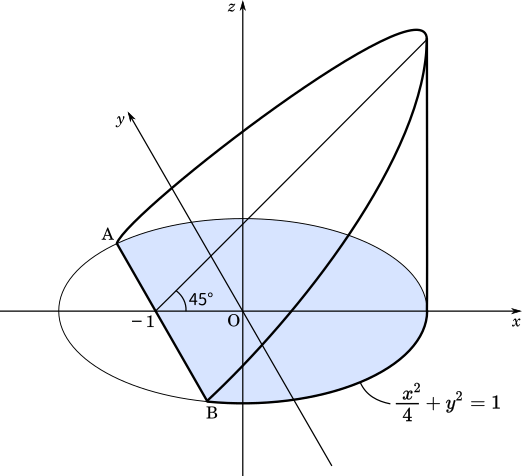
下の図で与えられた円柱を $45$°で切断した立体について考える。
(1) 青色で示された部分の面積を求めよ。
(2) 立体を平面 $x=t\enspace(-1<t<2)$ で切ったとき、断面の面積 $S(t)$ を $t$ を用いて表せ。
(3) 立体の体積を求めよ。（広島大・改）

---

楕円の面積を求める

まずは、底面の青色の部分の面積を求めましょう。底面は $\displaystyle \frac{x^2}{4}+{y^2}=1$ で表される楕円で、上から見ると次のようになります。

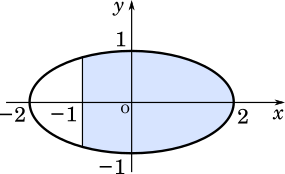
面積は積分を使って求めます。上下対象な図形なので上半分の面積を求めてそれを２倍します。

$\displaystyle \frac{x^2}{4}+y^2=1\\\displaystyle y^2=1-\frac{x^2}{4}\\\displaystyle y=\sqrt{1-\frac{x^2}{4}}\\\displaystyle y=\frac{1}{2}\sqrt{1-x^2}$

$\displaystyle S=2\int_{-1}^2 \frac{1}{2}\sqrt{4-x^2}dx\\\displaystyle=\int_{-1}^2\sqrt{4-x^2}dx$

一度 $\sin$ で置換してみると分かるのですが計算が非常に煩雑になってしまいます。そこで $\cos$ で置換すると積分区間の片方が $0$ になって計算しやすくなるのです。

$x=2\cos u$ とすると
$x:-1\rightarrow2\\\displaystyle u:\frac{2}{3}\pi\rightarrow0$

また $dx=-2\sin u\enspace du$ より
$\displaystyle S=\int_{\frac{2}{3}\pi}^0\sqrt{4-4\cos^2 u}\cdot(-2\sin u)du\\\displaystyle=-\int_0^{\frac{2}{3}\pi} 2\sqrt{1-\cos^2 u}\cdot(-2\sin u)du\\\displaystyle=4\int_0^{\frac{2}{3}\pi} \sin^2 u\enspace du$

そしてここで半角の公式を使います。
$\displaystyle \sin^2u=\frac{1-\cos2u}{2}$ より
$\displaystyle S=2\int_0^{\frac{2}{3}\pi} 1-\cos 2u\enspace du\\\displaystyle=2\left[u-\sin2u\cdot\frac{1}{2}\right]_0^{\frac{2}{3}\pi}\\\displaystyle=2\left(\frac{2}{3}\pi-\frac{1}{2}\sin\frac{4}{3}\pi\right)\\\displaystyle=\frac{4}{3}\pi-\left(-\frac{\sqrt{3}}{2}\right)\\\displaystyle =\frac{4}{3}\pi+\frac{\sqrt{3}}{2}$

（答え）

断面を四角形にする

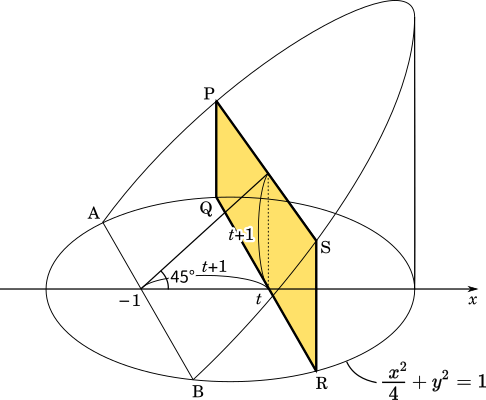
次に断面の面積 $S(t)$ を求めます。断面を四角形 PQRS とします。45°で切断しているので四角形の高さ PQ は $-1$ から $t$ までの距離と同じです。よって $t-(-1)=t+1$ です。

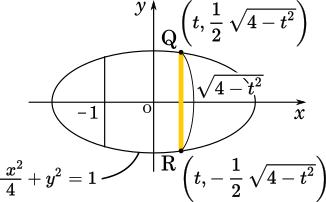
上から見た図で考えると四角形の横の長さ QR は $\sqrt{4-t^2}$ となります。よって四角形の面積は
$S(t)=\sqrt{4-t^2}(t+1)$（答え）

積分で体積を求める

ここから積分で体積を求めます。参考書などにはスマートな解き方が掲載されていますが、ここでは教科書の知識を使い倒して強引に攻め落とす方針でいきます。

先ほど求めた四角形の面積を $-1$ から $2$ の範囲で積分すれば体積が求められます。

$\displaystyle\int_{-1}^2\sqrt{4-t^2}(t+1)dt$
いったん展開して式を２つに分けます。
$\displaystyle\int_{-1}^2t\sqrt{4-t^2}+\sqrt{4-t^2}dt\\\displaystyle=\int_{-1}^2t\sqrt{4-t^2}dt+\int_{-1}^2\sqrt{4-t^2}dt\\$
ここで $\displaystyle\int_{-1}^2\sqrt{4-t^2}dt\\$ は(1)でやった積分と同じなので $\displaystyle\frac{4}{3}\pi+\frac{\sqrt{3}}{2}$ です。あとは $\displaystyle\int_{-1}^2t\sqrt{4-t^2}dt$ を求めていきます。
ここも先ほどと同じで $\cos$ 置換の方が計算が速いです。
$t=2\cos u$ として
$t:-1\rightarrow 2\\\displaystyle u:\frac{2}{3}\pi\rightarrow 0$
また $dt=-2\sin u\enspace du$ だから
$\int_{-1}^2t\sqrt{4-t^2}dt\\\displaystyle=\int_{\frac{2}{3}\pi}^02\cos u\sqrt{4-\cos^2 u}(-2\sin u)du\\\displaystyle=-\int_0^{\frac{2}{3}\pi}2\cos u\cdot2\sqrt{1-\cos^2 u}(-2\sin u)du\\\displaystyle=8\int_0^{\frac{2}{3}\pi}\sin^2u\cos u\enspace du\\\displaystyle$

$\displaystyle=4\int_0^{\frac{2}{3}\pi}2\sin u\cos u\cdot\sin u\enspace du\\\displaystyle=4\int_0^{\frac{2}{3}\pi}\sin 2u\sin u\enspace du$

ここで
$ \cos(2u+u)=\cos 2u\cos u-\sin 2u\sin u\cdots\text{①}\\\cos(2u-u)=\cos 2u\cos u+\sin 2u\sin u\cdots\text{②}$
①－②を計算すると
$\cos 3u-\cos u=-2\sin2u\sin u\\\displaystyle\sin2u\sin u=-\frac{1}{2}(\cos 3u-\cos u)$
よって
$\displaystyle =-2\int_0^{\frac{2}{3}\pi}\cos 3u-\cos u\enspace du\\\displaystyle=-2\left[\sin 3u\cdot\frac{1}{3}-\sin u\right]_0^{\frac{2}{3}\pi}\\\displaystyle=-2\left(\frac{1}{3}\sin 2\pi-\sin\frac{2}{3}\pi\right)\\\displaystyle=-2\left(0-\frac{\sqrt{3}}{2}\right)=\sqrt{3}$
合計して
$\displaystyle V=\sqrt{3}+\frac{4}{3}\pi+\frac{\sqrt{3}}{2}=\frac{4}{3}\pi+\frac{3\sqrt{3}}{2}$

（答え）