【数Ⅱ円と直線】直線を円で切り取る　二等辺三角形を作って解決

円 $C:x^2+y^2=4$ と直線 $l:y=m(x-4)$ が異なる２点 $P,Q$ で交わっているとき、次の問いに答えよ。

(1) 定数 $m$ のとりうる値の範囲を求めよ。
(2) $l$ が $C$ によって切りとられる線分の長さが $2$ であるとき $m$ の値を求めよ。

$m$ の範囲を求める

まず、$x^2+y^2=4$ は原点を中心とする半径 $2$ の円になります。また、$y=m(x-4)$ は、点 $(4,0)$ を通り、傾きが $m$ の直線です。

図で表すとこのようになります。

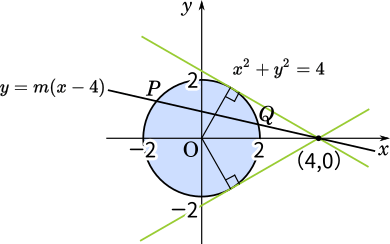
直線は $m$ の値によって傾きが変化します。そのうち緑で引いた２本の直線は円と１点で接しています。よって、傾きがこの２本の間にあるときに円と異なる２点で交わることになります。

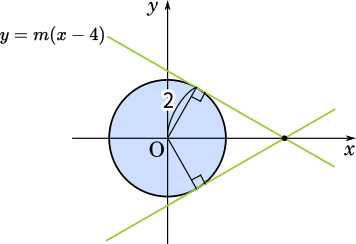
ここで原点と直線の距離を考えると円の半径になるので、距離は $2$ です。

公式に当てはめるために直線の式を変形します。
$y=m(x-4)\\y=mx-4m\\mx-y-4m=0$
公式に当てはめると
$\displaystyle\frac{|m\cdot0-1\cdot0-4m|}{\sqrt{m^2+1^2}}<2$
これを計算して $m$ の範囲を求めます。
$\displaystyle\frac{|-4m|}{\sqrt{m^2+1}}<2$
不等式なので、正の数と負の数に注意します。

左辺の $\displaystyle\frac{|-4m|}{\sqrt{m^2+1}}$ は、$m$ がマイナスの値でも、$m^2$ でプラスになるので、$\sqrt{m^2+1}$ もプラスになります。よって、両辺に $\sqrt{m^2+1}$ をかけても不等号の向きは変わりません。
$|-4m|<2{\sqrt{m^2+1}}$
そして、この式も両辺ともプラスの値なので２乗しても不等号の向きは変わりません。よって
$16m^2<4(m^2+1)\\4m^2<m^2+1\\3m^2-1<0\\\displaystyle m^2-\frac{1}{3}<0\\\displaystyle\left(m+\sqrt{\frac{1}{3}}\right)\left(m-\sqrt{\frac{1}{3}}\right)<0\\\displaystyle-\frac{\sqrt{3}}{3}<m<\frac{\sqrt{3}}{3}$

（答え）

円を直線で切りとるときの長さ

(2) に進みます。

このような問題が出された時には直角三角形を作るのがコツです。

$\triangle OPQ$は二等辺三角形です。点 $P,Q$ の中点を $M$ とすると直角三角形$\triangle OMQ$ ができます。問題文より、$PQ=2$ なので $MQ=1$、$OQ$ は半径なので $OQ=2$ です。ここから三平方の定理を使って

$OM^2+1^2=2^2\\OM^2=4-1\\OM^2=3\\OM=\sqrt{3}\enspace(OM>0)$

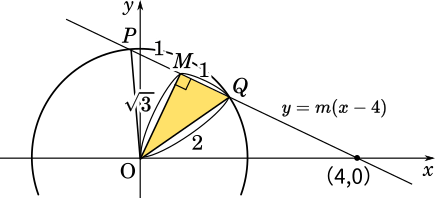
点と直線の公式に当てはめていきましょう。

$\displaystyle\frac{|m\cdot0-1\cdot0-4m|}{\sqrt{m^2+1}}=\sqrt{3}\\\displaystyle\frac{|-4m|}{\sqrt{m^2+1}}=\sqrt{3}\\\displaystyle|-4m|=\sqrt{3(m^2+1)}$
両辺を２乗して
$16m^2=3(m^2+1)\\16m^2=3m^2+3\\13m^2-3=0\\\displaystyle m^2-\frac{3}{13}=0\\\displaystyle\left(m+\sqrt{\frac{3}{13}}\right)\left(m-\sqrt{\frac{3}{13}}\right)=0\\\displaystyle m=\pm\frac{3\sqrt{13}}{13}$

（答え）

直線を円で切りとるときに、二等辺三角形を作るというのは直感でひらめくものではないのでテクニックとして暗記しておくべき事項です。