【数Bベクトル】たとえで分かるベクトルの引き算　直接行くか寄り道するか

逆ベクトルの和として考える

ベクトルの引き算を説明する方法の一つは逆ベクトルを用いるものです。ベクトルを逆向きにしたものが逆ベクトルでした。

例えば、$\overrightarrow{OA}-\overrightarrow{OB}$は、$\overrightarrow{OA}+(-\overrightarrow{OB})$ と考えることができます。

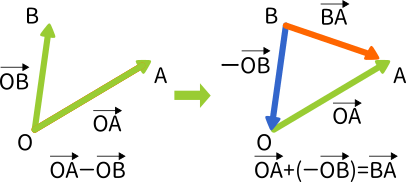
よって、$\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OA}+(-\overrightarrow{OB})=\overrightarrow{BA}$ となります。

ベクトルはスタート地点とゴール地点のみを考える

例えば、自宅からBさん宅へ行くとします。そのとき、Bさん宅へ直接行くルートと、いったんAさん宅に寄ってからBさん宅へ向かうルートがあります。

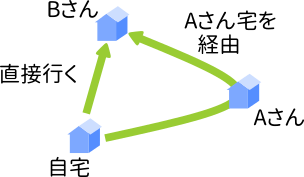
ベクトルの世界ではスタート地点とゴール点だけを考えます。自宅がスタート地点でBさん宅がゴール地点なので、上の２つのルートは同じものと見なします。これは式で表すと、

$\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{OB}$

と言うことです。

もう少し言うと、Bさん宅へ向かうルートはいくらでも作ることができます。それでもゴール地点がBさん宅である以上は、全て $\overrightarrow{OB}$ と同じであると考えるのです。

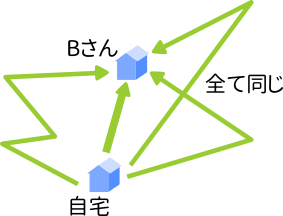
Aさん宅からBさん宅を引くと

再び $\overrightarrow{OA}-\overrightarrow{OB}$ を考えてみましょう。下の図で言うとこれは、自宅→Aさん宅から自宅→Bさん宅をひく、ということです。

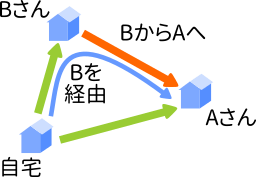
先ほど述べたようにAさん宅までのルートは一つではありませんでした。「自宅→Aさん宅」は他に何もなければ一直線のルートで良いのですが、そこにBさん宅が登場したことによってBさん宅を経由することになったのです。