【数Ⅲ複素数平面】１のn乗根を利用して円周の長さを求める

$n$を自然数とする、このとき、次の問いに答えなさい。(山口大)

(1) 方程式$z^n=1$の解をすべて求め、極形式で表しなさい。ただし、解$z$の偏角$\theta$は$0 \text{≦} x \text{≦} 2\pi$とする。

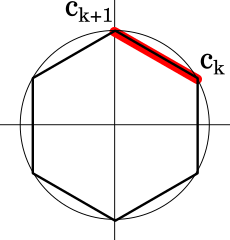
(2) (1)で得られた解を偏角が小さい順に$c_0,c_0,c_1,c_2,\dots,c_{n-1}$とおく。このとき、すべての$k=0,1,2,\dots,n-2$に対して、$|c_{k+1}-c_k|=\sqrt{2\left(1-\cos{\frac{2\pi}{n}}\right)}$が成り立つことを示しなさい。ただし、$c_n=c_0$とする。

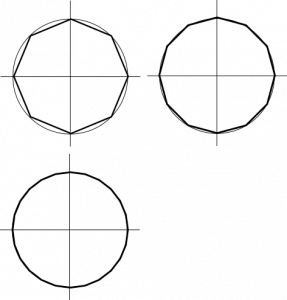
(3) (2)の$c_k$に対して、$\displaystyle S_n=\sum_{k=0}^{n-1}|c_{k+1}-c_k|$とするとき、$\displaystyle\lim_{n\rightarrow\infty}S_n$を求めなさい。

$z^3=1$とかでもヤバいのに、$n$乗って、どうするんですか？

3乗根のときは解の数は3個だったじゃない？
$n$乗根の場合、解は$n$個ある。
$n$の値によって解の個数が変わるから、$k$を使って、$n$個のうちの$k$番目、という形で書いてやればいいのよ。

イメージわかない。

要は教科書通りの式を書けってこと。
$z^n=r^n(\cos\theta+i \sin\theta)^n$から、
$r=1$ってのと、ド・モアブルで
$z^n=\cos n\theta+i\sin n\theta$
ここで$z^n=1$で、1っていう数はいいかえると$1+0\cdot i$ってことだから、
$\cos n\theta=1$　かつ　$\sin n\theta=0$で、
どっちも成り立つのは、$n\theta=0$のとき。
ここから、$n\theta=2k\pi$
$\displaystyle\theta=\frac{2k\pi}{n}$ってすればよかった。

教科書に書いてあることまんま！

まま。で、これを最初の式に代入して、
$\displaystyle z^n=\left(\cos\frac{2k\pi}{n}+i \sin\frac{2k\pi}{n}\right)^n$
$\displaystyle z=\cos\frac{2k\pi}{n}+i \sin\frac{2k\pi}{n}$
ここで、気を付けないといけないのは、
$k=n$のとき$\displaystyle\frac{2k\pi}{n}$は$2\pi$になって、ちょうど一周回って$n=0$のときとカブるから、$k$の範囲$0$から$n-1$になるから注意ね。

最後にトラップ！

これも教科書まま。よって、
$\displaystyle z=\cos\frac{2k\pi}{n}+i \sin\frac{2k\pi}{n}$
$(k=0,1,2,\dots,n-1)$　(解答)

(2)

で、(2)は？

とりあえず絶対値のまんまだとどうにもならんから、絶対値が出てくる公式は何だっけ？

んー、$z\overline{z}=|z|^2$？

そうそう、それくらいのもの。で、
$|c_{k+1}-c_k|^2=(c_{k+1}-c_k)(\overline{c_{k+1}-c_k})$
ってするの。
展開すると、
$c_{k+1}\overline{c_{k+1}}-\overline{c_k}c_{k+1}-c_k\overline{c_{k+1}}+c_k\overline{c_k}$
ここで、
$c_{k+1}\overline{c_{k+1}}=|c_{k+1}|^2=1$，
$c_{k}\overline{c_{k}}=|c_{k}|^2=1$
ってなるから、
$=2-\overline{c_k}c_{k+1}-c_k\overline{c_{k+1}}$

なんで$|c_{k+1}|^2=1$なの？

教科書戻って。(1)から$c_k$は1の$n$乗根で、1の$n$乗根は半径1の円周上の点だったろ？　複素平面で絶対値って原点からの距離のことだから、1になるの。

あー、そうだった。

ここで、
$\displaystyle c_k=\cos\frac{2k\pi}{n}+i \sin\frac{2k\pi}{n}$、
$\displaystyle c_{k+1}=\cos\frac{2(k+1)\pi}{n}+i \sin\frac{2(k+1)\pi}{n}$
式書くのメンドイから、
$\displaystyle \frac{2k\pi}{n}=A,\frac{2(k+1)\pi}{n}=B$
とする。
ここで、上の式の
$2-\overline{c_k}c_{k+1}-c_k\overline{c_{k+1}}$
に代入して$2-(\cos A-i\sin A)(\cos B+i\sin B)$
$-(\cos A+i\sin A)(\cos B+i sin B)$
展開して
$2-(\cos A\cos B+i\cos A\sin B-i\sin A\cos B+\sin A\sin B)$
$-(\cos A\cos B-i\cos A\sin B+i\sin A\cos B+\sin A\sin B)$

で、こっからどうするの？

最終的に、$\displaystyle \sqrt{2 \left( 1-\cos{\frac{2\pi}{n}}\right)}$に持ち込みたいの。でも、この式$k$がないじゃない？なんとかして$k$消さないといけないの。

消えるの？

消えるよ。
$\displaystyle B-A=\frac{2(k+1)\pi}{n}-\frac{2k\pi}{n}=\frac{2\pi}{n}$
で消える。

はあ。で？

ちなみにだけど、$\cos(A-B)$は？

加法定理でしょ。シンコスコスシン。

そうそう。だた、コサインのときはコスコスシンシン。
$\cos(B-A)=\cos A\cos B+\sin A\sin B$
で、加法定理使って式を整理すると
$2-2\cos(B-A)$
になる。

計算したら、$2-2\cos(A-B)$になったけど。

でも、$\cos x=\cos (-x)$が成り立つから、$\cos(A-B)=\cos(B-A)$でいいのよ。

また、トラップきた！

国公立２次試験レベルは総合力試されるから、がんばれ。

よって

$\displaystyle |c_{k+1}-c_k|=\sqrt{2 \left( 1-\cos{\frac{2\pi}{n}} \right)}$　(解答)

(3)

式にルートがついててメンドイから一度、式を整理する。

$\displaystyle |c_{k+1}-c_k|^2=2\left(1-\cos\frac{2\pi}{n}\right)$
$\displaystyle =4\left(\frac{1-cos\frac{2\pi}{n}}{2}\right)=4\sin^2\frac{\pi}{n}$

半角の公式。$\displaystyle \sin^2 x=\frac{1-\cos 2x}{x}$

よって、$\displaystyle |c_{k+1}-c_k|=2\sin\frac{\pi}{n}$

ここから、
$\displaystyle S_n=\sum_{k=0}^{n-1}|c_{k+1}-c_k|=\sum_{k=0}^{n-1}2\sin\frac{\pi}{n}=2n\sin\frac{\pi}{n}$

なんで？っていうか、式に$k$ないし。

なくてもいいの。シグマは「繰り返し足せ！」ってことだから、$k=1$から$n$ってなってたら、$n$倍してやればいいの。で、$k=0$から$n-1$までだったら、やっぱり$n$倍でオッケー。

0から始めるから1個増えるのね。

そういうこと。だから、$k$が0から$n-1$に変化するってことは、$n$個足せってことだから、$\displaystyle 2n\sin\frac{\pi}{n}$になるの。

あとは、

$\displaystyle\lim_{n\rightarrow\infty}S_n=\lim_{n\rightarrow\infty}2n\frac{\pi}{n}\frac{\sin\frac{\pi}{n}}{\frac{\pi}{n}}=\lim_{n\rightarrow\infty}2{n}\frac{\pi}{n}\cdot1=2\pi$　(解答)

最後の計算が分からない。

公式

$\displaystyle\lim_{x\rightarrow0}\frac{\sin x}{x}=1$

要は分母と分子の$x$に同じ形の式が入ればいいの。今回は$\displaystyle \sin\frac{\pi}{n}$ってなってるから分母と分子を$\displaystyle \frac{\pi}{n}$に揃えてるの。で、勝手に分母作っちゃったから、つじつま合わせで分数の前に$\displaystyle \frac{\pi}{n}$を置く。

公式と違って$\lim$が$\rightarrow 0$じゃなくて$\rightarrow\infty$ですよね。

そこ大事。$n\rightarrow\infty$のとき、$\displaystyle \frac{\pi}{n}\rightarrow0$ってなるでしょ？これで公式と同じことになる。

で、オマケの話。

そもそも、$|c_{k+1}-c_k|$って図で示すとこうなる。

正$n$角形の1辺の長さが$|c_{k+1}-c_k|$[te]それを$n$個足し合わせるってことは、要は多角形の辺の長さの合計ってこと。で、$n$をどんどん増やしていくと。

円になった！

最終的に、円周の長さと一致する。半径1の円の周の長さは$2\pi$だから解答と一致する。

なるほど。ってことはホントは最初から答えが$2\pi$って分かってたってことね。