【数Ⅲ微分の応用】ざっくりイメージから漸近線を導く

増減表を作る

問題　関数 $\displaystyle y=\frac{x^2}{x-1}$ の増減、グラフの凹凸、漸近線を調べてグラフの概形をかけ。

---

こういう形が来たら、まずは分母をチェックするようにしましょう。$x$ に $1$ を代入すると分母が $0$ になってしまうので、式が成り立ちません。よって、
$\displaystyle y=\frac{x^2}{x-1}\enspace (x\ne 1)$
となります。

ここから増減表を作るために、$y’,y”$ を求めていきましょう。
$\displaystyle y’=\frac{(x^2)'(x-1)-x^2(x-1)’}{(x-1)^2}$

$\displaystyle =\frac{2x(x-1)-x^2}{(x-1)^2}$
$\displaystyle=\frac{2x^2-2x-x^2}{(x-1)^2}$
$\displaystyle=\frac{x^2-2x}{(x-1)^2}$
また
$\displaystyle y”=\frac{(x^2-2x)'(x-1)^2-(x^2-2x)\{(x-1)^2\}’}{(x-1)^4}$
$\displaystyle =\frac{(2x-2)(x-1)^2-(x^2-2x)\cdot2(x-1)}{(x-1)^4}$
$\displaystyle=\frac{(2x-2)(x-1)-2(x^2-2x)}{(x-1)^3}$
$\displaystyle=\frac{2x^2-2x-2x+2-2x^2+4x}{(x-1)^3}$
$\displaystyle=\frac{2}{(x-1)^3}$

次に極値を求めます。
$y’=0$ のとき
$\displaystyle \frac{x^2-2x}{(x-1)^2}=0$
$x^2-2x=0$
$x(x-2)=0$
$x=0,2$

ここから極値を求めると、$\displaystyle f(0)=0,\enspace f(2)=4$

プラスマイナスの条件を考える

次に導関数の＋－の条件を考えます。

$\displaystyle y’=\frac{x^2-2x}{(x-1)^2}$ について考えてみると、分母は２乗しているので $x$ にどんな値が入ろうと常に＋になります。プラス×プラス＝プラス、マイナス×マイナス＝プラスでした。

あとは分子の符号によって＋－が決まるので、分子の方に適当に色々な値を放り込んでみましょう。$x^2-2x$ において $x$ に $-1$ を代入すると、$3$ になるので＋の値です。あとは $x=2$ で極値をとるので、それの右側の $x=3$ あたりで考えます。そうすると $ 3^2-2\times3=3$ となり＋の値となります。

これで増減表の $f'(x)$ の部分は完成です。

次に $f”(x)$ を考えます。$\displaystyle y”=\frac{2}{(x-1)^3}$ は分母が＋になる場合とーになる場合があるので気を付けましょう。＋の３乗は＋になるし、ーの３乗はーになります。例えば、$(-2)^3=-8$ です。

分母は $x$ が $1$ のときを境目にして、＋とーに分かれます。よって
$x<1$ のとき $y”<0$
また
$x>1$ のとき $y”>0$
となります。これで増減表の材料がそろいました。

$x$	$\cdots$	0	$\cdots$	1	$\cdots$	2	$\cdots$
$f'(x)$	＋	0	ー	/	ー	0	＋
$f”(x)$	ー	ー	ー	/	＋	＋	＋
$f(x)$		極大 0		/		極小 4

不定形の解消

あとは漸近線を求めてグラフの完成です。

実際に計算してみましょう。しかし $\displaystyle y=\frac{x^2}{x-1}$ は $x\rightarrow\infty$ とすると $\displaystyle \frac{\infty}{\infty}$ となります。いわゆる不定形というヤツです。

こうなった場合は不定形を解消していきます。
方針としては、とにかく約分したいから分子にムリヤリ $x-1$ を作ります。
$\displaystyle y=\frac{x^2}{x-1}$
$\displaystyle=\frac{x^2-2x+1+2x-1}{x-1}$

これで $2x$ と $1$ はお互いに打消しあって元の式と同じことになります。ここから
$\displaystyle =\frac{(x-1)^2+2x-1}{x-1}$
$\displaystyle=\frac{(x-1)^2}{x-1}+\frac{2x}{x-1}-\frac{1}{x-1}$
$\displaystyle =x-1+\frac{2x}{x-1}-\frac{1}{x-1}$

これでもまだ真ん中の項が不定形なので、さらに分子にムリヤリ $x-1$ を作ります。
$\displaystyle=x-1+\frac{2x-2+2}{x-1}-\frac{1}{x-1}$
$\displaystyle=x-1+\frac{2(x-1)+2}{x-1}-\frac{1}{x-1}$

$\displaystyle =x-1+\frac{2(x-1)}{x-1}+\frac{2}{x-1}-\frac{1}{x-1}$
$\displaystyle=x-1+2+\frac{1}{x-1}$
$\displaystyle=x+1+\frac{1}{x-1}$
これで不定形が解消できました。

$x=1$ の漸近線

次に極限をとって、$x=1$ が漸近線であることを示します。

$\displaystyle \lim_{x\rightarrow1+0} x+1+\frac{1}{x-1}$

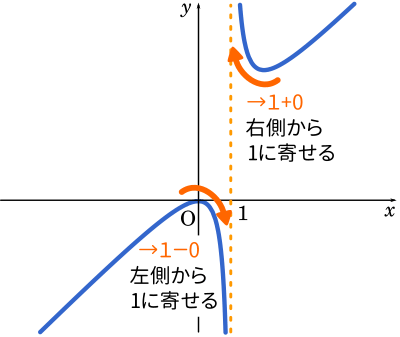
あとはイメージです。$\displaystyle\frac{1}{x-1}$ の $x$ を 右側から $1$ に寄せていきます。
$\displaystyle \frac{1}{2-1}=1\\\displaystyle\frac{1}{1.1-1}=10\\\displaystyle\frac{1}{1.01-1}=100$
このようにざっくりイメージで言うと、$1$ に近づくにつれ値は大きくなりそうです。よって
$\displaystyle \lim_{x\rightarrow1+0} x+1+\frac{1}{x-1}=\infty$
今度は左側から $1$ に寄せてみましょう。
$\displaystyle \frac{1}{0-1}=-1\\\displaystyle\frac{1}{0.9-1}=-10\\\displaystyle\frac{1}{0.99-1}=-100$
よって
$\displaystyle \lim_{x\rightarrow1-0} x+1+\frac{1}{x-1}=-\infty$
これで、左右から考えて ∞ に発散することが分かったので、$x=1$ は漸近線であるということができます。

$x+1$ の漸近線

そして $\displaystyle x+1+\frac{1}{x-1}$ から、$y=x+1$ という漸近線を作ることができます。

$x$ を $+\infty$ の方向にふってみましょう。$x$ に大きな値を代入してみます。

$\displaystyle 101+1+\frac{1}{101-1}=101+1+0.01\\\displaystyle10001+1+\frac{1}{10001-1}=10001+1+0.0001\\\displaystyle 1000001+1+\frac{1}{10000001-1}=10000001+1+0.0000001$

このように $x$ が大きな値になるほど、$x+1$ に近づいていきます。

よって、$x+1$ も漸近線になります。以上よりグラフを描くと

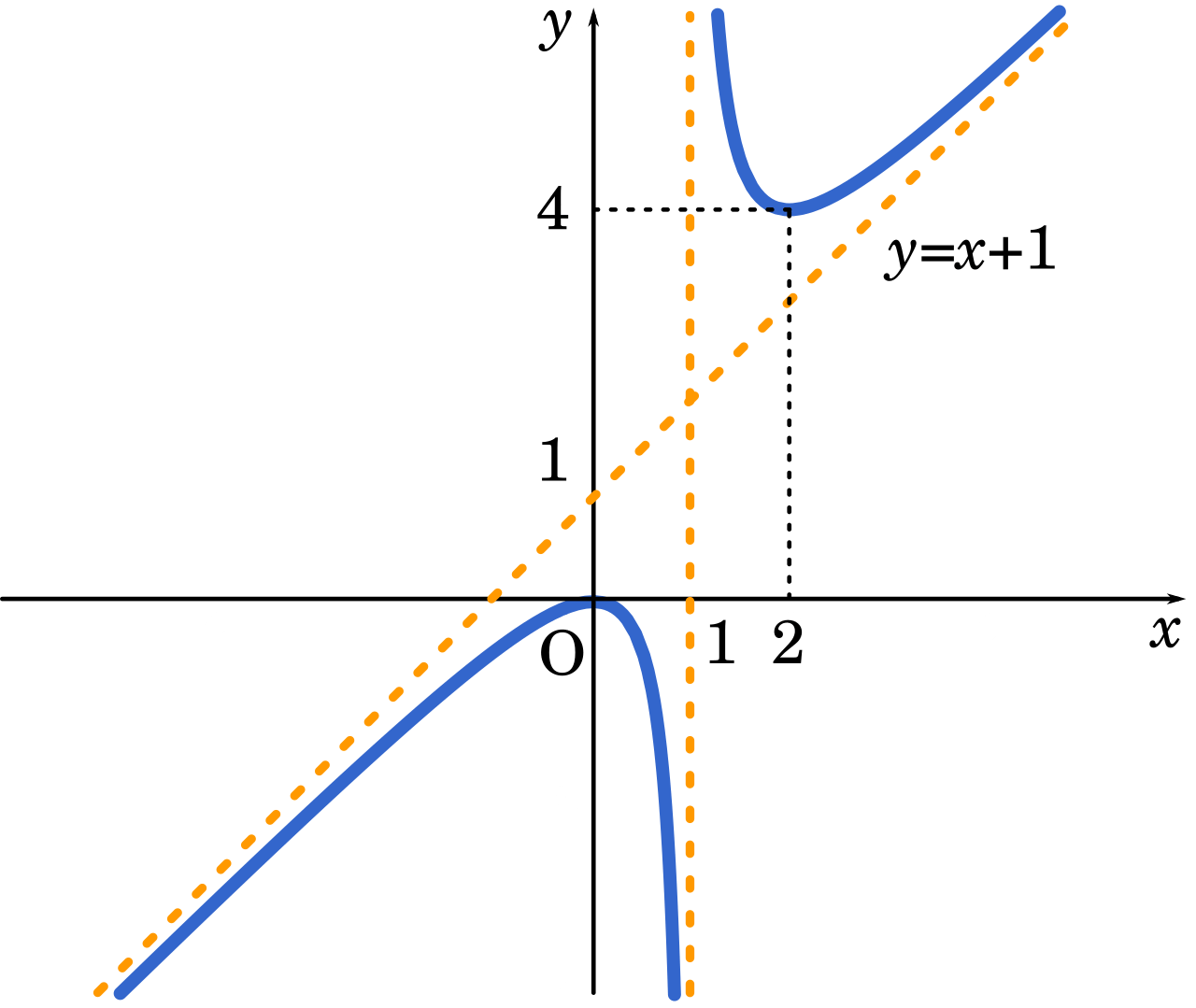
もう少し正確に言うと

問題は解けましたが、最後に参考書などに載っている $\displaystyle\lim_{x\rightarrow\infty}\{f(x)-(ax+b)\}=0$ について考えてみましょう。

今回の問題では $\displaystyle f(x)=x+1+\frac{1}{x-1}$、$ax+b=x+1$ ということになります。そして式はそれぞれ $y$ 座標を表していて $y=f(x)$、$y=x+1$ です。図で表すと

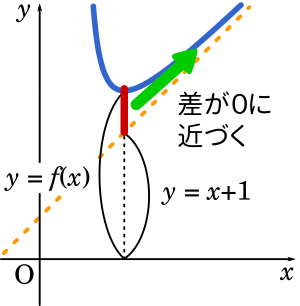
$f(x)-(x+1)$ はグラフの赤い部分を指しています。これは右にいくほど小さくなっていき、限りなく $0$ に近づいていくはずです。式で示すと

$\displaystyle \lim_{x\rightarrow\infty} x+1+\frac{1}{x-1}-(x+1)\\\displaystyle=\lim_{x\rightarrow\infty} \frac{1}{x-1}\\=0$

このことより、2つのグラフの差が $0$ に近づいていくので、$y=x+1$ は漸近線であるということができるのです。