【数Ⅲ複素数平面】点wの表す図形 zを消去して解決
複素数平面上の点 $z$ が原点を中心とする半径 $\sqrt{2}$ の円周上を動くとする。このとき、次の問いに答えよ。(静岡大2017)
(1) 複素数$\displaystyle w=\frac{z-1}{z-i}$ で表される点 $w$ の描く図形を複素数平面上に図示せよ。ただし、$i$ は虚数単位とする。
(2) (1)の図形を、原点を中心に$\displaystyle\frac{\pi}{6}$だけ回転して得られる図形を求めよ。


z =の式に変形してzを消去する
$w$ が $z$ で表されている場合、このままではどういう図形になるか分からないので、何とかして $z$ を消去します。
問題文より、半径が $\sqrt{2}$ であることから
$|z|=\sqrt{2}$
です。

$\displaystyle w=\frac{z-1}{z-i}$
$(z-i)w=z-1$
$zw-iw=z-1$
$zw-z=iw-1$
$z(w-1)=iw-1$
$\displaystyle z=\frac{iw-1}{w-1}\enspace(w\ne1)$


$\displaystyle|z|=\left|\frac{iw-1}{w-1}\right|\\\displaystyle\sqrt{2}=\left|\frac{iw-1}{w-1}\right|\\\displaystyle2=\left|\frac{iw-1}{w-1}\right|^2\\2|w-1|^2=|iw-1|^2$
バー(棒)の扱い方
ここで、公式 $z\bar z=|z|^2$ より
$2(w-1)(\overline{w-1})=(iw-1)(\overline{iw-1})\\2(w-1)(\bar w-1)=(iw-1)(-i\bar w-1)$

バー(棒)は共役な複素数を表す記号で、例えば $5+3i$ の共役な複素数は $5-3i$ となります。つまり実数の符号はそのまま、虚数の部分の符号は反対にするということです。
$\overline{iw-1}$ で考えてみましょう。まず、これを分割して$\bar i\bar w-\bar 1$ とします。$i$ は虚数だから $\bar i=-i$、$w$ は文字の中に実数と虚数を含むので $\bar w$ と表すしかありません。$1$ は実数のみの数なので $\bar 1=1$ で符号は変わりません。結果、$-i\bar w-1$ となるのです。
計算を進めます。
$2(w-1)(\bar w-1)=(iw-1)(-i\bar w-1)\\2w\bar w-2w-2\bar w+2=w\bar w-iw+i\bar w+1\\w\bar w-(2-i)w-(2+i)\bar w+1=0$
カギとなる因数分解

因数分解をして $(w+\circ\circ)(\bar w+\circ\circ)$ のような形にも持ち込みます。


ここで、
$(w+a)(\bar w+b)=w\bar w+bw+a\bar w+ab$
として、先ほどの式と比較します。
$w\bar w+bw+a\bar w+ab\\w\bar w-(2-i)w-(2+i)\bar w+1=0$
上下で比較すると $a=-(2+i),b=-(2-i)$ とすることで因数分解できそうです。しかし、$(w-2-i)(\bar w-2+i)$ は展開すると $(2+i)(2-i)$ が余計な部分として出てくるので、引き算をすることでつじつま合わせをします。
$w\bar w-(2-i)w-(2+i)\bar w+1=0$
$(w-2-i)(\bar w-2+i)-(2+i)(2-i)+1=0$
$(w-2-i)(\bar w-2+i)=(2+i)(2-i)-1$
$(w-2-i)(\bar w-2+i)=4+1-1=4$
$(w-2-i)(\overline{w-2-i})=4$
ここで、$z\bar z=|z|^2$ より
$|w-2-i|^2=4\\|w-2-i|=2$



よって、点 $ w$ は点 $2+i$ を中心とする半径 $2$ の円上を動く。
(答え)
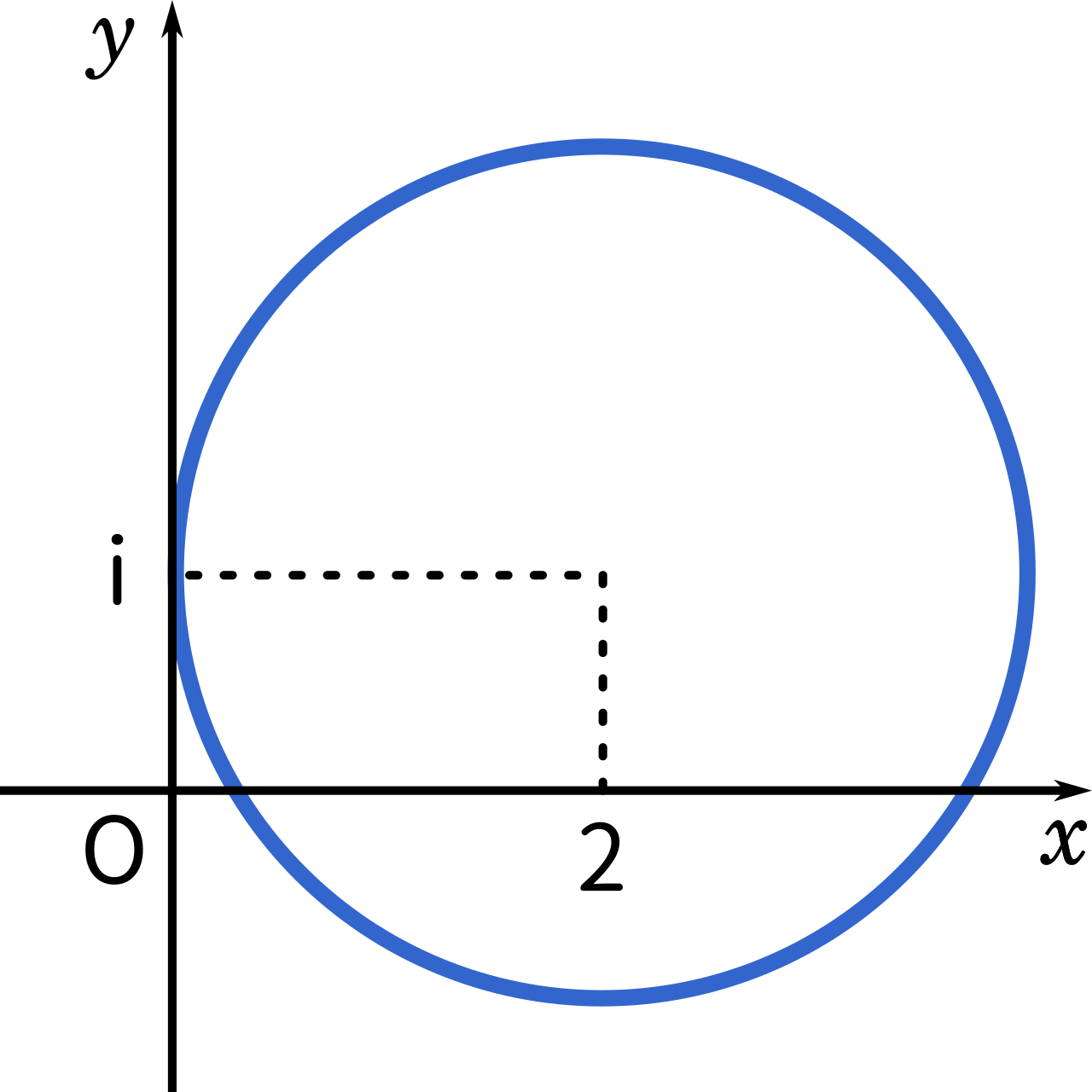
円の中心を基準に回転させる
次に、(2) を考えます。
(1) でできた円を回転させるのですが、これは円の中心を $\displaystyle\frac{\pi}{6}$ 回転させて半径2の円を作る、と考えればよいです。
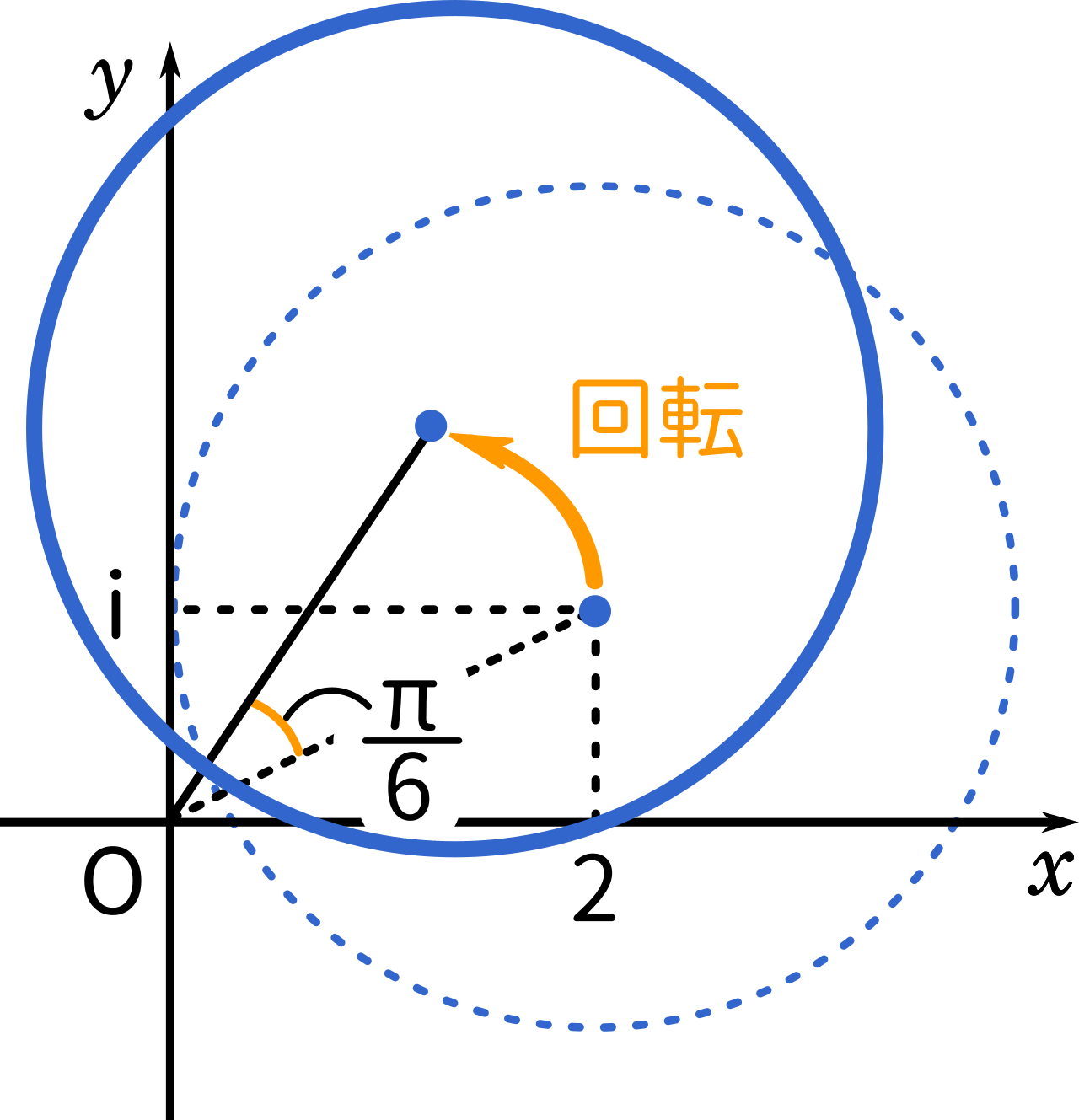

$\displaystyle\frac{\pi}{6}$ を極座標にしてかけ算します。
$\displaystyle (2-i)\left(\cos \frac{\pi}{6}+i\sin\frac{\pi}{6}\right)\\\displaystyle=(2+i)(\frac{\sqrt{3}}{2}+\frac{1}{2}i)\\\displaystyle=\sqrt{3}+i+\frac{\sqrt{3}}{2}i-\frac{1}{2}\\\displaystyle=\sqrt{3}-\frac{1}{2}+(1+\frac{\sqrt{3}}{2})i$
(答え) $\displaystyle\sqrt{3}-\frac{1}{2}+(1+\frac{\sqrt{3}}{2})i$ を中心とする半径2の円
(2) はただ回転するだけなので、大した問題ではありませんが、コツが必要なのは (1) です。$w$ が $z$ で表されている式では
① とにかく邪魔な $z$ を消去したい。
② だからいっぺん $z=$ の式に変形して、
③ $z$ を数字に置きかえて消去!
という手順で作戦を立てましょう。
SNSでシェア