【スマホで読む・わかりやすい】共通テスト数学IIB2022本試【解説・正解・問題】

第１問　正解
(ア,イ) (2, 5)　ウ 5　エ 3
オ 0　カ 0　キ,ク 1,2　ケ 1
コ, サ 4, 3　シ 5　ス 2　セ 8
ソ 1　タ 1　チ 3　ツ 0　テ 2

〔１〕(1)

$D:x^2+y^2-4x-10y+4\leqq0$

$x$ と $y$ について平方完成して円の方程式に持ち込むと良い。

$(x-2)^2-4+(y-5)^2-25+4\leqq0$
$(x-2)^2+(y-5)^2\leqq25$
$(x-2)^2+(y-5)^2\leqq5^2$

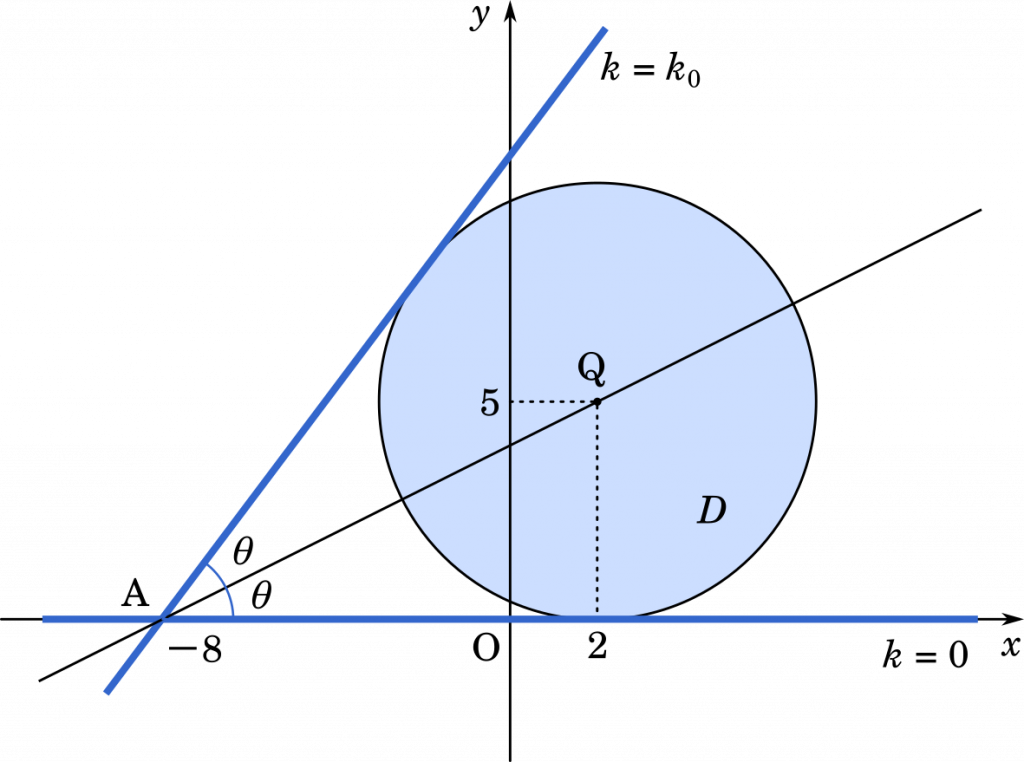
よって，領域 $D$ は，中心が点 $(2,5)$，半径が 5 の円の③周および内部である。

・・・ア,イ,ウ,エ

(2)(i)

(1)により，直線 $y=0$ は点 A を通る $C$ の接線の一つとなることがわかる。

・・・オ

(2)(ii)

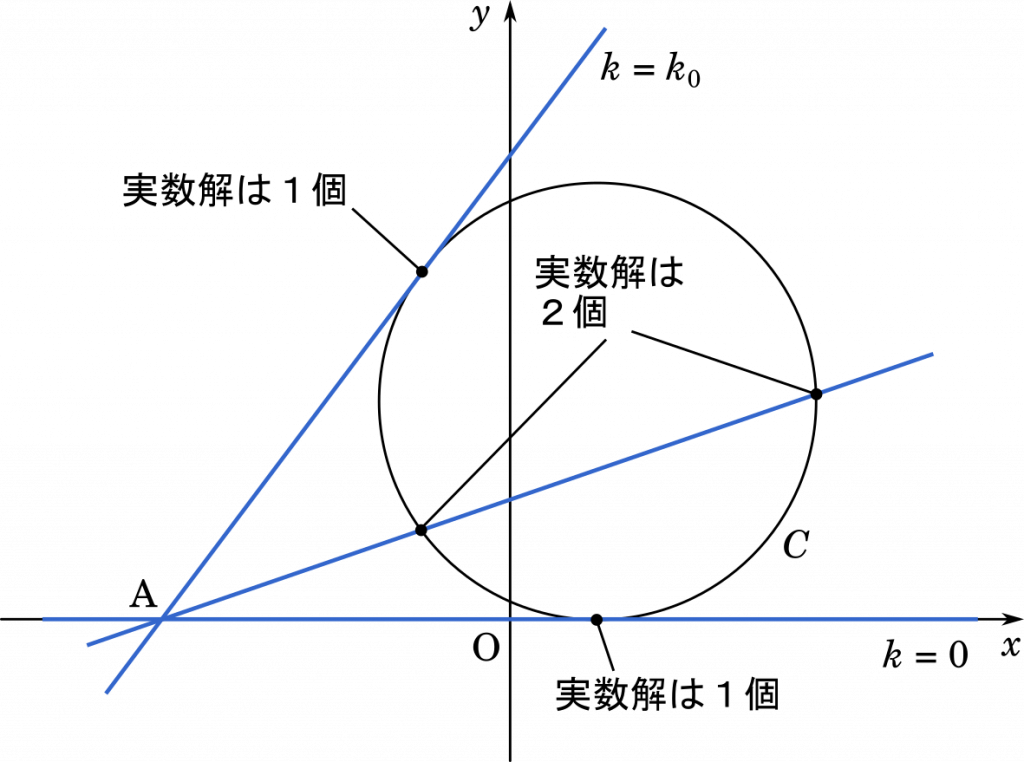
直線と円の式を連立して，$x$ についての方程式をつくる。この方程式が $\textsf{\textcircled{0}}$ 重解をもつとき，直線 $\ell$ は円 $C$ の接線となる。

・・・カ

(2)(iii)

$\tan\theta=\cfrac{5}{2-(-8)}=\cfrac{5}{10}=\cfrac{1}{2}$

・・・キ,ク

また，直線 $y=0$ と異なる接線の傾きは $\tan2\theta$ と表すことができる。

・・・ケ

(2)(iv)

接線傾きが $k_0$ のとき，接線と $x$ 軸のなす角は $2\theta$ だから，$2\theta=\theta+\theta$ として

$k_0=\tan(\theta+\theta)$
$=\cfrac{\tan\theta+\tan\theta}{1-\tan\theta\tan\theta}$
$=\cfrac{2\tan\theta}{1-\tan^2\theta}$
$=\cfrac{2\cdot\cfrac{1}{2}}{1-\Big(\cfrac{1}{2}\Big)^2}$
$=\cfrac{1}{1-\cfrac{1}{4}}$
$=\cfrac{\enspace1\enspace}{\cfrac{3}{4}}$
$=\cfrac{1\times4}{\cfrac{3}{4}\times4}$
$=\cfrac{4}{3}$

・・・コ,サ

直線 $\ell$ と領域 $D$ が共有点をもつような $k$ の値の範囲は⑤$0\leqq k\leqq k_0$ である。

・・・シ

〔２〕(1)

$\log_39=3$

・・・ア

$\log_{\small{\frac{1}{4}}}x=-\cfrac{3}{2}$

とすると

$x=\Big(\cfrac{1}{4}\Big)^{\small{-\frac{3}{2}}}$
$=4^{\small{\frac{3}{2}}}$
$=2^3=8$

・・・セ

(2)

$\log_ab=t$ ・・・①

より

$a^t=b$

・・・ソ

$\log_ba=\cfrac{1}{t}$ ・・・②

より

$a=b^{\small{\frac{1}{t}}}$

・・・タ

(3)

③と④より，$\log_ab>\log_ba$ すなわち $t>\cfrac{1}{t}$ を満たすのは，$1<t<0$，$1<t$ のときであることがわかる。

これをもとに，$a>1$ のときを考える。

まず，$\log_ab=t$ について，$t>1$ のときを考える。

ここは，ためしに具体的な値を当てはめて考えてみると良い。

たとえば，$a=2,t=2$ とすると

$b=2^2=4$

となるので，$a<b$ である。

次に，$-1<t<0$ のときを考える。

たとえば，$a=2,t=-\cfrac{1}{2}$ とすると

$b=2^{\small{-\frac{1}{2}}}$
$=\Big(\cfrac{1}{2}\Big)^{\small{\frac{1}{2}}}$
$=\cfrac{1}{2^{\small{\frac{1}{2}}}}$

となる。

$\cfrac{1}{a}=\cfrac{1}{2}$ と $\cfrac{1}{2^{\small{\frac{1}{2}}}}$ を比べると

$\cfrac{1}{2}<\cfrac{1}{2^{\small{\frac{1}{2}}}}$
$\cfrac{1}{a}<b$

が成り立つことがわかる。

また，$a$ が 1 以上で，$t$ が負の値であれば，$b$ は 1 より小さくなる。

したがって

③ $\cfrac{1}{a}<b<1$，$a<b$

が適する。

・・・チ

今度は，$0<a<1$ のときを考える。

まず，$t>1$ の例として，$a=\cfrac{1}{2}$，$t=2$ とすると

$b=\Big(\cfrac{1}{2}\Big)^2=\cfrac{1}{4}$

となるので，$b<a$ である。

また，$b$ は真数条件より $0<b$ である。

次に，$-1<t<0$ のときを考える。

たとえば，$a=\cfrac{1}{2}$，$t=-\cfrac{1}{2}$ とすると

$b=\Big(\cfrac{1}{2}\Big)^{-\small{\frac{1}{2}}}=2^{\small{\frac{1}{2}}}$

となるので，$b<\cfrac{1}{a}$ が成り立つ。

したがって

$\textsf{\textcircled{0}}$ $0<b<a$，$1<b<\cfrac{1}{a}$

が適する。

・・・ツ

(4)

(3)の条件を整理すると

$a>1$ のとき

$\cfrac{1}{a}<b<1$ または $a<b$

$0<a<1$ のとき

$0<b<a$ または $1<b<\cfrac{1}{a}$

ならば

$\log_ab>\log_ba$

が成り立つ。

$q$ が 1 より大きい値なので，$a=q=\cfrac{12}{11},b=p=\cfrac{12}{13}$ とすると

$\cfrac{1}{a}<b<1$ は

$\cfrac{11}{12}<\cfrac{12}{13}<1$

となるので，$\log_pq<\log_qp$

が成り立つ。

$\cfrac{12}{11}$ と $\cfrac{12}{13}$ を比べるときには分母の値を合わせると良い。

$\cfrac{11}{12},\cfrac{12}{13}$
$\cfrac{11\cdot13}{12\cdot13},\cfrac{12\cdot12}{12\cdot13}$
$\cfrac{143}{12\cdot13},\cfrac{144}{12\cdot13}$

となるので，$\cfrac{11}{12}<\cfrac{12}{13}$ である。

次に，$r$ が 1 より大きい値なので，$a=r=\cfrac{14}{13},b=p=\cfrac{12}{13}$ とすると

$0<b<a$ は

$0<\cfrac{12}{13}<\cfrac{14}{13}$

となるので

$\log_pr>\log_rp$

が成り立つ。よって②が正しい。

・・・テ

問題文

第１問

〔１〕 座標平面上に点 A$(-8,0)$ をとる。また，不等式

$x^2+y^2-4x-10y+4<\leqq0$
の表す領域を $D$ とする。

(1) 領域 $D$ は，中心が点 $(\boxed{\enspace\textsf{ア}\enspace},\boxed{\enspace\textsf{イ}\enspace})$，半径が $\boxed{\enspace\textsf{ウ}\enspace}$ の円の $\boxed{\boxed{\enspace\textsf{エ}\enspace}}$ である。

$\boxed{\boxed{\enspace\text{エ}\enspace}}$ の解答群

以下，点$(\boxed{\enspace\text{ア}\enspace},\boxed{\enspace\text{イ}\enspace})$ を Q とし，方程式

$x^2+y^2-4x-10y+4=0$
の表す図形を $C$ とする。

(2) 点 A を通る直線と領域 $D$ が共有点をもつのはどのようなときかを考えよう。

(i) (1) により，直線 $y=\boxed{\enspace\textsf{オ}\enspace}$ は点 A を通る $C$ の接線の一つとなることがわかる。

太郎さんと花子さんは点 A を通る $C$ のもう一つの接線について話している。

点 A を通り，傾きが $k$ の直線を $\ell$ とする。

(ii) 太郎さんの求め方について考えてみよう。

$y=k(x+8)$ を $x^2+y^2-4x-10y+4=0$ に代入すると，$x$ についての 2 次方程式

$(k^2+1)x^2+(16k^2-10k-4)x+64k^2-80k+4=0$

が得られる。この方程式が $\boxed{\boxed{\enspace\textsf{カ}\enspace}}$ ときの $k$ の値が接線の傾きとなる。

$\boxed{\boxed{\enspace\text{カ}\enspace}}$ の解答群

(iii) 花子さんの求め方について考えてみよう。

$x$ 軸と直線 AQ のなす角を $\theta\Big(0<\theta\leqq\cfrac{\pi}{2}\Big)$ とすると

$\tan\theta=\cfrac{\boxed{\enspace\textsf{キ}\enspace}}{\boxed{\enspace\textsf{ク}\enspace}}$

であり，直線 $y=\boxed{\enspace\text{オ}\enspace}$ と異なる接線の傾きは $\tan\boxed{\boxed{\enspace\textsf{ケ}\enspace}}$ と表すことができる。

$\boxed{\boxed{\enspace\text{ケ}\enspace}}$ の解答群

(iv) 点 A を通る $C$ の接線のうち，直線 $y=\boxed{\enspace\text{オ}\enspace}$ と異なる接線の傾きを $k_0$ とする。このとき，(ii)または(iii)の考え方を用いることにより

$k_0=\cfrac{\boxed{\enspace\textsf{コ}\enspace}}{\boxed{\enspace\textsf{サ}\enspace}}$

であることがわかる。

直線 $ell$ と領域 $D$ が共有点をもつような $k$ の値の範囲は

$\boxed{\boxed{\enspace\textsf{シ}\enspace}}$ である。

$\boxed{\boxed{\enspace\text{シ}\enspace}}$ の解答群

〔２〕 $a,b$ は正の実数であり，$a\not=1,b\not=1$ を満たすとする。太郎さんは $\log_ab$ と $\log_ba$ の大小関係を調べることにした。

(1) 太郎さんは次のような考察をした。

まず，$\log_39=\boxed{\enspace\textsf{ス}\enspace}$，$\log_93=\cfrac{1}{\boxed{\enspace\text{ス}\enspace}}$ である。この場合

$\log_39>\log_93$

が成り立つ。

一方，$\log_{\small{\frac{1}{4}}}\boxed{\enspace\textsf{セ}\enspace}=-\cfrac{3}{2}$，$\log_{\boxed{\text{セ}}}\cfrac{1}{4}=-\cfrac{2}{3}$ である。この場合

$\log_{\small{\frac{1}{4}}}\boxed{\enspace\text{セ}\enspace}<\log_{\boxed{\text{セ}}}\cfrac{1}{4}$

が成り立つ。

(2) ここで

$\log_ab=t$　・・・①
とおく。

(1)の考察をもとにして，太郎さんは次の式が成り立つと推測し，それが正しいことを確かめることにした。

$\log_ba=\cfrac{1}{t}$ ・・・②

① により，$\boxed{\boxed{\enspace\textsf{ソ}\enspace}}$ である。このことにより $\boxed{\boxed{\enspace\textsf{タ}\enspace}}$ が得られ，②が成り立つことが確かめられる。

$\boxed{\boxed{\enspace\text{ソ}\enspace}}$ の解答群

$\boxed{\boxed{\enspace\text{タ}\enspace}}$ の解答群

(3) 次に太郎さんは(2)の考察をもとにして

$t>\cfrac{1}{t}$　・・・③

を満たす実数 $t(t\not=0)$ の値の範囲を求めた。

この考察により，③を満たす $t(t\not=0)$ の値の範囲は

$-1<t<0,1<t$

であることがわかる。

ここで，$a$ の値を一つ定めたとき，不等式

$\log_ab>\log_ba$　・・・・④

を満たす実数 $b(b>0,b\not=1)$ の値の範囲について考える。

④を満たす $b$ の値の範囲は，$a>1$ のときは $\boxed{\boxed{\enspace\textsf{チ}\enspace}}$ であり，$0<a<1$ のときは $\boxed{\boxed{\enspace\textsf{ツ}\enspace}}$ である。

$\boxed{\boxed{\enspace\text{チ}\enspace}}$ の解答群

$\boxed{\boxed{\enspace\text{ツ}\enspace}}$ の解答群

(4) $p=\cfrac{12}{13},q=\cfrac{12}{11},r=\cfrac{14}{13}$ とする。

次の $\textsf{\textcircled{0}}$ ～ ③ のうち，正しいものは $\boxed{\boxed{\enspace\textsf{テ}\enspace}}$ である。

$\boxed{\boxed{\enspace\text{テ}\enspace}}$ の解答群